
1.9. Интервальные оценки
ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
Интервальное оценивание параметров распределения генеральной совокупности состоит в построении доверительных интервалов.
Доверительным интерваломдля
параметра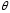 называется интервал
называется интервал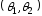 ,
содержащий истинное значение параметра
с заданной вероятностью
,
содержащий истинное значение параметра
с заданной вероятностью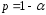 .
Таким образом,
.
Таким образом,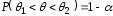 .
Число
.
Число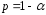 называетсядоверительной вероятностью,
а значение
называетсядоверительной вероятностью,
а значение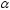 –уровнем значимости.
–уровнем значимости.
При построении доверительных интервалов
вводят в рассмотрение специально
подобранную статистику
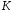 ,
распределение которой известно. Наиболее
распространенными являются статистики,
имеющие нормальное, Стьюдента и
,
распределение которой известно. Наиболее
распространенными являются статистики,
имеющие нормальное, Стьюдента и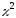 распределения.
распределения.
Методика построения доверительных интервалов для отдельных параметров распределения генеральной совокупности зависит как от вида распределения, так и от знания значений остальных параметров закона распределения.
1.9.1.Рассмотрим задачу построениядоверительного интервала для
математического ожидания
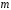 нормально распределенной генеральной
совокупности при неизвестной дисперсии.
нормально распределенной генеральной
совокупности при неизвестной дисперсии.
Пусть случайная величина
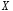 имеет нормальное распределение с
параметрами
имеет нормальное распределение с
параметрами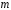 и
и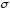 .
Найдем доверительный интервал для
математического ожидания
.
Найдем доверительный интервал для
математического ожидания в предположении, что дисперсия
в предположении, что дисперсия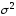 неизвестна и задан уровень значимости
неизвестна и задан уровень значимости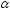 .
.
Английский математик Госсет (псевдоним
Стьюдент) доказал, что статистика
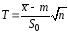 имеет распределение Стьюдента с
имеет распределение Стьюдента с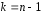 степенями свободы. Так как кривая
плотности вероятностей распределения
Стьюдента симметрична относительно
степенями свободы. Так как кривая
плотности вероятностей распределения
Стьюдента симметрична относительно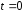 ,
будем искать доверительную область в
виде:
,
будем искать доверительную область в
виде: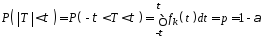 .
.
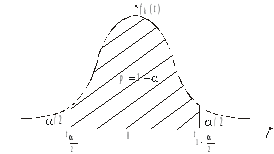
Рис. 11 - Геометрическое пояснение смысла квантилейраспределения Стьюдента
Из рисунка 11 видно, что площадь под
графиком каждого из симметричных
«хвостов» будет равна
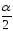 ,
тогда значения границ интервала совпадут
с квантилями
,
тогда значения границ интервала совпадут
с квантилями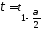 и
и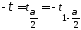 .
.
В таблице П 4 Приложения приведены
значения
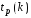 в зависимости от доверительной вероятности
в зависимости от доверительной вероятности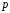 и числа степеней свободы
и числа степеней свободы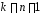 .
Можно также использовать функцию
СТЬЮДРАСПОБР пакета прикладных программEXCEL.
.
Можно также использовать функцию
СТЬЮДРАСПОБР пакета прикладных программEXCEL.
Таким образом, получаем:
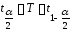 или
или
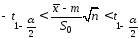 .
.
Подставив в полученное неравенство
значения
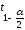 ,
,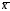 ,
,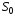 ,
,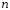 и разрешив это неравенство относительно
и разрешив это неравенство относительно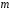 ,
получим доверительный интервал для
неизвестного математического ожидания
,
получим доверительный интервал для
неизвестного математического ожидания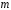 нормально распределенной случайной
величины
нормально распределенной случайной
величины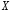 с неизвестной дисперсией
с неизвестной дисперсией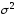 и заданным уровнем значимости
и заданным уровнем значимости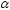 :
: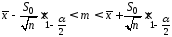 .
.
ПРИМЕР 6
Требуется построить доверительный
интервал для математического ожидания
нормально распределенной генеральной
совокупности с параметрами
 и
и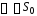 для уровней значимости
для уровней значимости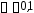 ,
,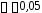 и
и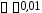 при неизвестной дисперсии.
при неизвестной дисперсии.
Общее выражение для доверительного интервала в данном случае имеет вид:
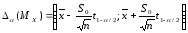
Вычислим этот интервал для различных уровней значимости.
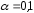 :
: ,
,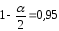 ,
,
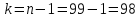 – число степеней свободы.
– число степеней свободы.
Так как в таблице П4 Приложения нет числа
степеней свободы
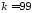 ,
то для вычисления
,
то для вычисления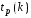 можно воспользоваться следующим методом:
можно воспользоваться следующим методом:
Статистическая функция СТЬЮДРАСПОБР
пакетаEXCELдает значение
квантили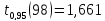 .
Нужно иметь в виду, что вEXCELвычисляются значения двусторонних
«антиквантилей»
.
Нужно иметь в виду, что вEXCELвычисляются значения двусторонних
«антиквантилей»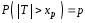 .
Поэтому чтобы получить значение
односторонней квантили
.
Поэтому чтобы получить значение
односторонней квантили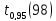 ,
нужно в этой функции задать вероятность
,
нужно в этой функции задать вероятность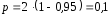 (см. справку к функции СТЬЮДРАСПОБР).
(см. справку к функции СТЬЮДРАСПОБР).
В дальнейших расчетах используем значения, даваемые EXCEL.
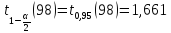 ,
,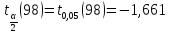 .
.
Подставим
значения этих квантилей и вычисленные
ранее значения
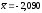 и
и
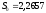 в
формулу доверительного интервала:
в
формулу доверительного интервала:
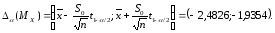

Таким образом, неизвестное математическое
ожидание
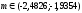 с вероятностью
с вероятностью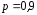 .
.
Аналогично найдем доверительные
интервалы для математического ожидания
для уровней значимости
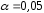 и
и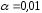 .
.
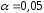 :
: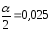 ,
,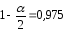 ,
,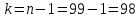 ,
,
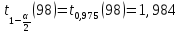 ,
,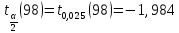 ,
,

Таким образом, неизвестное математическое
ожидание
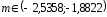 с
вероятностью
с
вероятностью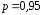 .
.
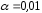 :
: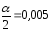 ,
,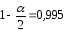 ,
,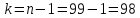 ,
,
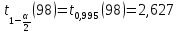 ,
,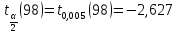 ,
,
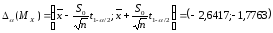 .
.
Таким образом, неизвестное математическое
ожидание
 с вероятностью
с вероятностью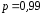 .
.
1.9.2.Определим теперьдоверительный
интервал для неизвестной дисперсии
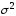 нормально распределенной случайной
величины
нормально распределенной случайной
величины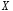 с неизвестным математическим ожиданием
и заданным уровнем значимости α.
с неизвестным математическим ожиданием
и заданным уровнем значимости α.
В этом случае рассматривается статистика
 ,
имеющая распределение
,
имеющая распределение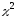 с
с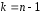 степенями свободы, где
степенями свободы, где – объем выборки.
– объем выборки.
Будем искать доверительную область в
виде: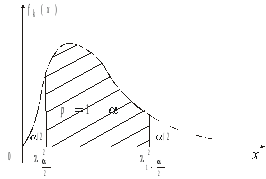
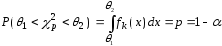
Рис. 12- Квантили распределения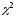
Как и в предыдущем случае, будем считать
площади под «хвостами» кривой распределения
равными по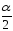 каждая
(рис. 12).
каждая
(рис. 12).
Тогда границы интервала совпадут с квантилями:
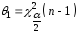 ,
,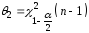 .
.
В таблице П5 Приложения приведены
значения
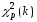 в зависимости от доверительной вероятности
в зависимости от доверительной вероятности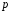 и числа степеней свободы
и числа степеней свободы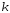 .
Можно также использовать функцию ХИ2ОБР
пакета прикладных программEXCEL.
.
Можно также использовать функцию ХИ2ОБР
пакета прикладных программEXCEL.
Таким образом, получаем
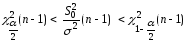 .
.
Подставив в полученное неравенство
значения
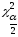 ,
,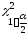 ,
, ,
,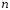 и разрешив это неравенство относительно
и разрешив это неравенство относительно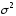 ,
получим доверительный интервал для
неизвестной дисперсии
,
получим доверительный интервал для
неизвестной дисперсии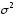 нормально распределенной случайной
величины
нормально распределенной случайной
величины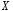 с неизвестным математическим ожиданием
и заданным уровнем значимости
с неизвестным математическим ожиданием
и заданным уровнем значимости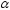 :
:
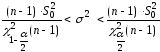 .
.
Следует отметить, что если математическое ожидание генеральной совокупности известно, то доверительный интервал для дисперсии будет иметь другой вид.
Длина доверительного интервала
характеризует точность оценивания и
зависит от объема выборки
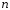 и доверительной вероятности
и доверительной вероятности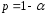 .
Чем меньше длина доверительного
интервала, тем надежнее оценка. При
увеличении объема выборки длина
доверительного интервала уменьшается.
.
Чем меньше длина доверительного
интервала, тем надежнее оценка. При
увеличении объема выборки длина
доверительного интервала уменьшается.
ПРИМЕР 7
Требуется построить доверительный
интервал для неизвестной дисперсии
нормально распределенной генеральной
совокупности с параметрами
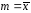 и
и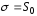 для уровней значимости
для уровней значимости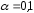 ,
,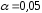 и
и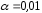 .
.
Для построения доверительного
интервала для неизвестной дисперсии
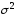 нормально распределенной генеральной
совокупности используется статистика
нормально распределенной генеральной
совокупности используется статистика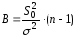 ,
имеющая распределение
,
имеющая распределение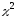 с
степенями свободы:
с
степенями свободы: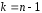
 .
.
Вычислим этот интервал для различных уровней значимости.
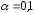 :
: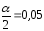 ,
,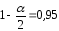 ,
,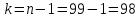 .
.
Так как в таблице П5 Приложения нет числа
степеней свободы
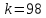 ,
то для вычисления
,
то для вычисления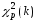 можно воспользоваться следующим методом:
можно воспользоваться следующим методом:
Статистическая функция ХИ2ОБР пакета EXCELдает следующие значения квантилей распределения «хи- квадрат»:
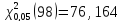 ,
,
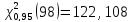 .
.
Следует иметь в виду, что в функции
ХИ2ОБР вычисляются «антиквантили»
 .
Чтобы получить значение квантили
.
Чтобы получить значение квантили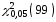 ,
нужно ввести обратную вероятность
,
нужно ввести обратную вероятность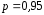 .
.
В дальнейших расчетах используются значения квантилей, вычисленные в EXCEL.
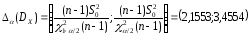
Таким образом, неизвестная дисперсия
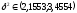 с
вероятностью
с
вероятностью .
.
Аналогично найдем доверительные
интервалы для дисперсии для уровней
значимости
 и
и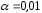 .
.
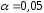 :
: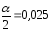 ,
,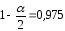 ,
,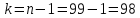 .
.
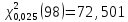 ,
,
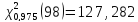 .
.
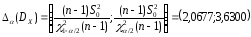
Таким образом, неизвестная дисперсия
 с
вероятностью
с
вероятностью .
.
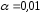 :
: ,
,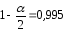 ,
,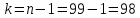 ,
,
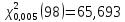 ,
,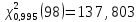 ,
,

Таким образом, неизвестная дисперсия
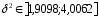 с вероятностью
с вероятностью .
.
Заметим, что выборочная дисперсия
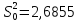 попадает
во все найденные доверительные интервалы,
причем, чем меньше уровень значимости
попадает
во все найденные доверительные интервалы,
причем, чем меньше уровень значимости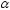 ,
тем больше длина соответствующего
доверительного интервала.
,
тем больше длина соответствующего
доверительного интервала.
