
1.6 Распределения и стьюдента
Рассмотрим некоторые виды специальных распределений, используемых в математической статистике. Сначала введем определение:
Квантилью, соответствующей
вероятности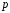 ,
называется такое значение
,
называется такое значение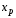 ,
при котором выполняется соотношение:
,
при котором выполняется соотношение:
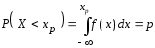 ,
,
где
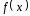 – плотность вероятностей соответствующего
закона распределения (слово квантиль
– женского рода). Геометрическое
пояснение смысла квантили, отвечающей
вероятности
– плотность вероятностей соответствующего
закона распределения (слово квантиль
– женского рода). Геометрическое
пояснение смысла квантили, отвечающей
вероятности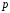 ,
приведено на рисунке 8.
,
приведено на рисунке 8.
РАСПРЕДЕЛЕНИЕ
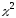
Пусть
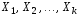 – нормально распределенные независимые
случайные величины, причем математическое
ожидание каждой из них равно нулю, а
среднеквадратическое отклонение –
единице, то есть
– нормально распределенные независимые
случайные величины, причем математическое
ожидание каждой из них равно нулю, а
среднеквадратическое отклонение –
единице, то есть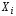
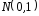 .
Тогда сумма квадратов этих величин
.
Тогда сумма квадратов этих величин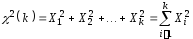 распределена по закону
распределена по закону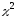 («хи
квадрат») с
(«хи
квадрат») с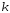 степенями свободы.
степенями свободы.
Рис. 7 - Графики плотности вероятностей
распределения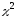

Плотность вероятностей этого распределения имеет вид:
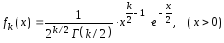 ,
,
где
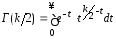 - гамма- функция.
- гамма- функция.
График плотности вероятностей
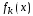 при малых
при малых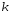 имеет длинный правый «хвост», а с ростом
имеет длинный правый «хвост», а с ростом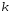 становится почти симметричным (рис. 7).
становится почти симметричным (рис. 7).
Квантили распределения
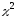 обозначаются
обозначаются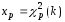 (рис. 8) и находятся по таблицам (таблица
П 5 Приложения).
(рис. 8) и находятся по таблицам (таблица
П 5 Приложения).
Рис. 8 - Геометрическое пояснение смысла
квантили
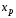 ,
,
отвечающей вероятности
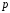
Распределение стьюдента
Пусть
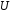 – нормально распределенная случайная
величина, причем
– нормально распределенная случайная
величина, причем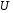
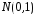 ,
а
,
а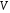 – независимая от
– независимая от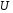 случайная величина, распределенная по
закону
случайная величина, распределенная по
закону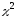 с
с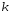 степенями свободы. Тогда известно, что
случайная величина
степенями свободы. Тогда известно, что
случайная величина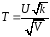 имеет
имеет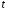 -распределение
или распределение Стьюдента с
-распределение
или распределение Стьюдента с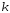 степенями свободы. Плотность вероятностей
этого распределения имеет вид:
степенями свободы. Плотность вероятностей
этого распределения имеет вид:
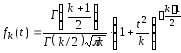 (рис. 9).
(рис. 9).
При
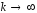 распределение Стьюдента стремится к
нормальному и при
распределение Стьюдента стремится к
нормальному и при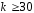 практически не отличается от нормального
практически не отличается от нормального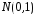 .
.
Квантили распределения Стьюдента
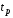 находят по таблицам (таблица П 4 Приложения)
в зависимости от вероятности
находят по таблицам (таблица П 4 Приложения)
в зависимости от вероятности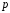 и числа степеней свободы
и числа степеней свободы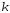 .
Так как график плотности вероятностей
распределения Стьюдента симметричен
относительно
.
Так как график плотности вероятностей
распределения Стьюдента симметричен
относительно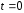 ,
то
,
то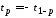 (рис. 9).
(рис. 9).
Квантили распределений Стьюдента и
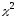 можно найти с помощью статистических
функций СТЬЮДРАСПОБР и ХИ2ОБР пакета
прикладных программEXCEL.
можно найти с помощью статистических
функций СТЬЮДРАСПОБР и ХИ2ОБР пакета
прикладных программEXCEL.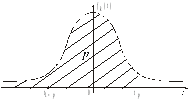
Рис. 9 - Плотность вероятностей и квантили распределения Стьюдента
1.7. Проверка статистических гипотез
Для получения обоснованных выводов о параметрах, виде распределения и других свойствах случайных величин необходимо проверить гипотезу о соответствии эмпирической функции распределения одному из известных теоретических законов.
Статистической гипотезойназывают любое утверждение о виде или о параметрах распределения генеральной совокупности. Например, статистическими являются гипотезы:
генеральная совокупность распределена по нормальному закону или любому другому конкретно заданному закону (гипотеза о виде распределения);
если известно, что генеральная совокупность распределена по нормальному закону, то параметры нормального закона равны выборочным характеристикам:
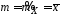 ,
,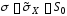 (параметрическая гипотеза).
(параметрическая гипотеза).
Гипотезу о виде распределения выдвигают на основе схожести гистограммы или полигона частот с соответствующей кривой одного из теоретических законов (нормального, равномерного, Пуассона и т. п.).
Когда предположение о виде распределения генеральной совокупности принято, следует проверить гипотезу о параметрах этого распределения.
Нулевой(основной) называют
выдвинутую гипотезу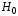 .
.
Альтернативныминазывают
гипотезы, которые противоречат нулевой.
Если отвергается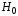 ,
то принимается одна из альтернативных
гипотез. При проверке статистических
гипотез могут быть допущены ошибки двух
родов с вероятностями:
,
то принимается одна из альтернативных
гипотез. При проверке статистических
гипотез могут быть допущены ошибки двух
родов с вероятностями:
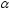 – вероятность отклонить гипотезу
– вероятность отклонить гипотезу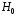 ,
при условии, что она верна (ошибка
первого рода);
,
при условии, что она верна (ошибка
первого рода);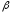 – вероятность принять гипотезу
– вероятность принять гипотезу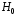 ,
при условии, что она неверна (ошибка
второго рода).
,
при условии, что она неверна (ошибка
второго рода).
Например, в радиолокации
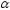 – вероятность пропуска сигнала,
– вероятность пропуска сигнала,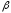 – вероятность ложной тревоги.
– вероятность ложной тревоги.
Ясно, что чем меньше будут ошибки первого
и второго рода, тем точнее статистический
вывод. Однако при заданном объеме выборке
одновременно уменьшить
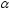 и
и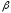 невозможно. Единственный способ
одновременного уменьшения
невозможно. Единственный способ
одновременного уменьшения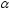 и
и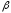 состоит в увеличении объема выборки.
состоит в увеличении объема выборки.
Если формулируется только одна гипотеза
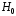 и требуется проверить, согласуются ли
статистические данные с этой гипотезой
или они ее опровергают, то критерии,
используемые для этого, называюткритериями согласия. В таких
критериях не выставляется конкретная
альтернативная гипотеза.
и требуется проверить, согласуются ли
статистические данные с этой гипотезой
или они ее опровергают, то критерии,
используемые для этого, называюткритериями согласия. В таких
критериях не выставляется конкретная
альтернативная гипотеза.
Прежде, чем привести схему статистической проверки гипотез, дадим используемые ниже определения новых понятий.
Статистикой критерияназывается
специально подобранная функция выборки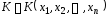 ,
которая служит для проверки гипотезы
,
которая служит для проверки гипотезы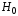 .
Статистика
.
Статистика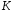 является мерой расхождения экспериментальных
данных с гипотетическим распределением.
является мерой расхождения экспериментальных
данных с гипотетическим распределением.
Как правило, перед анализом выборки
задается уровень значимости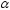 – вероятность ошибочного отклонения
нулевой гипотезы. Обычно полагают
– вероятность ошибочного отклонения
нулевой гипотезы. Обычно полагают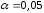 ,
,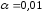 ,
,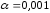 .
.
Критической областьюназывается
совокупность значений статистики, при
которых нулевая гипотеза отвергается.
Обычно критическую область выбирают
из условия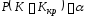 .
Критическую точку критерия
.
Критическую точку критерия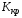 находят по соответствующим таблицам.
находят по соответствующим таблицам.
Схема статистической проверки гипотезы по критерию согласия:
формулировка нулевой
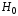 гипотезы;
гипотезы;выбор уровня значимости
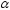 ;
;выбор статистики
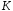 и соответствующего критерия;
и соответствующего критерия;определение критической области и области принятия гипотезы;
вычисление выборочной статистики
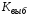 и проверка гипотезы;
и проверка гипотезы;принятие статистического решения.
