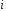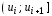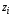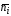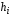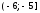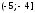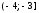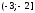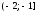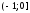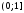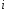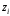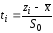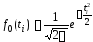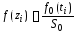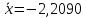1.4 Гистограмма и полигон частот
Пусть
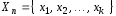 – выборка объема
– выборка объема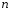 ,
содержащая
,
содержащая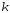 различных вариант, из генеральной
совокупности случайной величины
различных вариант, из генеральной
совокупности случайной величины с неизвестной плотностью вероятностей
с неизвестной плотностью вероятностей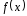 .
Приближением (оценкой) неизвестной
плотности вероятностей могут служитьгистограммаилиполигон
относительных частот. Гистограмма
и полигон относительных частот служат
для геометрического изображения
группированного вариационного ряда.
.
Приближением (оценкой) неизвестной
плотности вероятностей могут служитьгистограммаилиполигон
относительных частот. Гистограмма
и полигон относительных частот служат
для геометрического изображения
группированного вариационного ряда.
Гистограмма относительных частот
представляется в виде примыкающих друг
к другу прямоугольников с основаниями
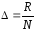 ,
равными ширине интервалов группировок,
и высотами
,
равными ширине интервалов группировок,
и высотами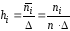 (рис. 1). Для гистограммы относительных
частот площадь ступенчатой фигуры
соответствует сумме вероятностей и
равна
(рис. 1). Для гистограммы относительных
частот площадь ступенчатой фигуры
соответствует сумме вероятностей и
равна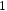 .
Площадь любого прямоугольника гистограммы
равна вероятности попадания значений
рассматриваемой случайной величины в
интервал, соответствующий основанию
прямоугольника.
.
Площадь любого прямоугольника гистограммы
равна вероятности попадания значений
рассматриваемой случайной величины в
интервал, соответствующий основанию
прямоугольника.
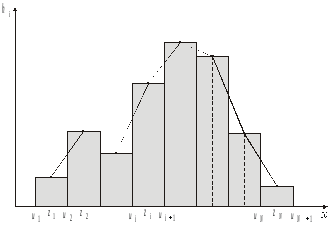
Рис. 1 - Гистограмма и полигон относительных частот
Полигоном относительных частотназывается ломаная, соединяющая точки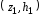 ,
,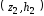 ,
…,
,
…,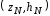 (рис. 1), где
(рис. 1), где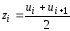 – середины интервалов группировки;
– середины интервалов группировки;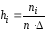 – высоты прямоугольников гистограммы.
– высоты прямоугольников гистограммы.
При увеличении объема выборки и уменьшении
длин интервалов гистограмма и полигон
относительных частот приближаются к
графику неизвестной функции
 – плотности вероятности генеральной
совокупности.
– плотности вероятности генеральной
совокупности.
По виду гистограммы или полигона частот
можно выдвинуть гипотезу о виде
распределения генеральной совокупности.
Например, если гистограмма имеет вид,
представленный на рис. 2а, то можно
предположить, что генеральная совокупность
имеет нормальный закон распределения
с плотностью вероятностей
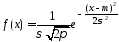 ;
рис. 2б – равномерное распределения с
плотностью вероятностей
;
рис. 2б – равномерное распределения с
плотностью вероятностей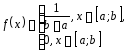 ; рис. 2в – показательное распределение
с плотностью вероятностей
; рис. 2в – показательное распределение
с плотностью вероятностей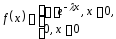 .
.

2а 2б 2в
Рис. 2Виды гистограмм
ПРИМЕР 3
Требуется построить гистограмму и
полигон относительных частот для
известного группированного вариационного
ряда. На их основе выдвинуть нулевую
гипотезу
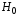 о виде распределения генеральной
совокупности. В данном случае это
нормальное распределение. На одном
чертеже с гистограммой построить график
теоретической плотности вероятностей.
Сделать вывод об их визуальном совпадении.
о виде распределения генеральной
совокупности. В данном случае это
нормальное распределение. На одном
чертеже с гистограммой построить график
теоретической плотности вероятностей.
Сделать вывод об их визуальном совпадении.
Для
удобства заполним таблицу. В таблицу
занесены середины интервалов
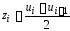 ,
в четвертый – относительные частоты
интервалов
,
в четвертый – относительные частоты
интервалов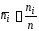 ,
в пятый – высоты прямоугольников
гистограммы относительных частот
,
в пятый – высоты прямоугольников
гистограммы относительных частот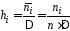 .
.
Таблица 6
|
Индекс
|
Интервал
|
Середина интервала
|
Относит. частота
|
Высота прямоуг.
| |
|
1 |
|
-5,5 |
0,0404 |
0,0404 | |
|
2 |
|
-4,5 |
0,1212 |
0,1212 | |
|
3 |
|
-3,5 |
0,1616 |
0,1616 | |
|
4 |
|
-2,5 |
0,2121 |
0,2121 | |
|
5 |
|
-1,5 |
0,2323 |
0,2323 | |
|
6 |
|
-0,5 |
0,1212 |
0,1212 | |
|
7 |
|
0,5 |
0,1010 |
0,1010 | |
|
8 |
|
1,5 |
0,0101 |
0,0101 | |
|
Сумма |
|
|
1 |
1 | |
По данным таблицы построим гистограмму.
Для этого в прямоугольной системе
координат на оси абсцисс откладываем
значения границ интервалов разбиения
и на каждом из интервалов с номером
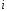 строим прямоугольник с высотой
строим прямоугольник с высотой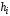 .
.
Для такой гистограммы площадь ступенчатой
фигуры соответствует сумме вероятностей
и равна
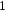 .
Площадь каждого прямоугольника
гистограммы равна вероятности попадания
случайной величины в интервал,
соответствующий основанию прямоугольника
.
Площадь каждого прямоугольника
гистограммы равна вероятности попадания
случайной величины в интервал,
соответствующий основанию прямоугольника
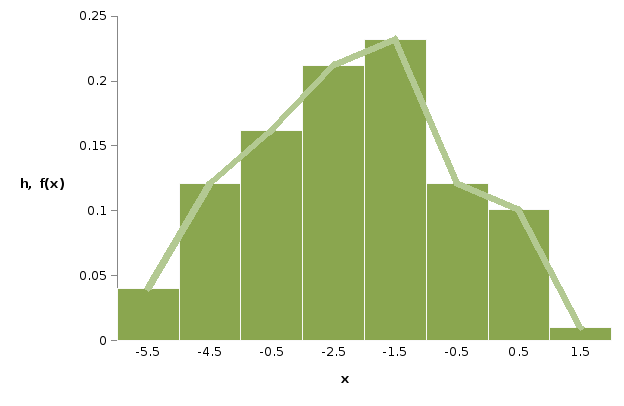
Рис.3. Гистограмма относительных частот и кривая теоритической плотности вероятностей
Полигон относительных частот – ломаная,
соединяющая точки
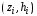 ,
,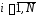
Гистограмма и полигон относительных
частот, являющиеся статистическими
оценками плотности вероятностей
генеральной совокупности, схожи с кривой
плотности вероятностей нормального
закона. На основании этого выдвигаем
нулевую гипотезу
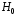 :
Генеральная совокупность, из которой
взята выборка, распределена по нормальному
закону с параметрами
:
Генеральная совокупность, из которой
взята выборка, распределена по нормальному
закону с параметрами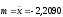 ,
,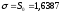 ,
то есть теоретическая плотность
вероятностей имеет вид:
,
то есть теоретическая плотность
вероятностей имеет вид: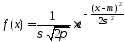
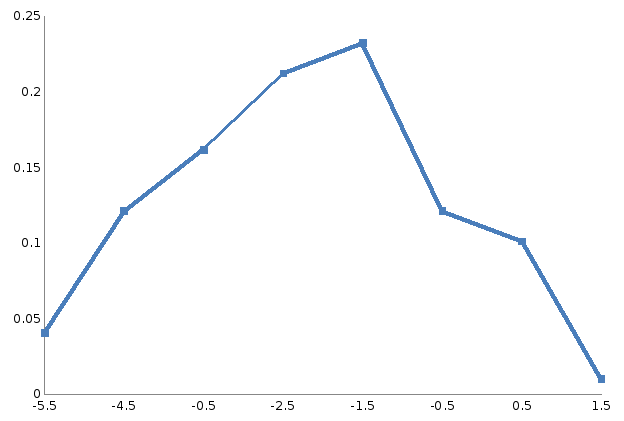
Рис.4 Полигон относительных частот
Вычислим значения теоретической
плотности вероятностей в точках
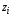 – середины интервалов по таблице П 2
Приложения. Результаты вычислений
занесем в таблицу. Заметим, что
– середины интервалов по таблице П 2
Приложения. Результаты вычислений
занесем в таблицу. Заметим, что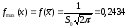 .
.
Таблица 7
|
|
|
|
|
| |
|
1 |
-5,5000 |
-2,0083 |
0,0531 |
0,0324 | |
|
2 |
-4,5000 |
-1,3980 |
0,1501 |
0,0916 | |
|
3 |
-3,5000 |
-0,7878 |
0,2925 |
0,1785 | |
|
4 |
-2,5000 |
-0,1776 |
0,3927 |
0,2396 | |
|
5 |
-1,5000 |
0,4326 |
0,3633 |
0,2217 | |
|
6 |
-0,5000 |
1,0429 |
0,2316 |
0,1413 | |
|
7 |
0,5000 |
1,6531 |
0,1017 |
0,0621 | |
|
8 |
1,5000 |
2,2633 |
0,0308 |
0,0188 | |
|
|
|
0,0000 |
0,3989 |
0,2434 | |
Из рисунка 3 видно, что график теоретической плотности вероятностей и гистограмма достаточно хорошо совпадают.