
Министерство образования и науки
Российской Федерации
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ
УНИВЕРСИТЕТ ИМЕНИ АКАДЕМИКА С.П. КОРОЛЕВА
(НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ)»
(СГАУ)
Кафедра высшей математики
Расчетно-графическая работа по высшей математике
«Статистический анализ одномерных данных»
Выполнила: Мытник С.Б.
524 группа
Вариант 15
Проверил: Бушков С.В.
Самара 2014г.
Введение
Математическая статистика – это прикладная математическая дисциплина, примыкающая к теории вероятностей. Она базируется на понятиях и методах теории вероятностей, но решает свои специфические задачи специальными методами.
Основная задача математической статистики – получить обоснованные выводы о параметрах, видах распределений и других свойствах случайных величин по конечной совокупности наблюдений над ними.
В расчетной работе рассматриваются основные методы анализа одномерных статистических данных: определение точечных и интервальных оценок параметров распределения, проверка гипотез о виде распределения. Рассматриваются также элементы корреляционного и регрессионного анализа двумерных статистических данных.
Задание
Дана выборка значений случайной величины
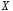 (выборка объема
(выборка объема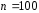 из генеральной совокупности).
из генеральной совокупности).
Найти выборочную оценку математического ожидания случайной величины
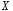 ,
указать свойства этой оценки.
,
указать свойства этой оценки.Найти выборочные оценки дисперсии и среднеквадратического отклонения случайной величины
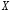 ,
указать свойства этих оценок.
,
указать свойства этих оценок.Составить группированный вариационный ряд, разбив выборку на
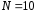 равных интервалов.
равных интервалов.Построить гистограмму и полигон относительных частот. На их основе выдвинуть нулевую гипотезу
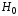 о виде распределения (нормальное
распределение).
о виде распределения (нормальное
распределение).На одном чертеже с гистограммой построить график теоретической плотности вероятностей. Сделать вывод об их визуальном совпадении.
Составить эмпирическую функцию распределения
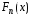 и построить ее график.
и построить ее график.На одном чертеже с эмпирической функцией распределения построить график теоретической функции распределения в соответствии с выдвинутой гипотезой
 .
Сделать вывод о визуальном совпадении
графиков эмпирической и теоретической
функции распределения.
.
Сделать вывод о визуальном совпадении
графиков эмпирической и теоретической
функции распределения.С помощью критерия согласия
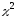 Пирсона проверить гипотезу
Пирсона проверить гипотезу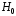 о виде распределения генеральной
совокупности для уровня значимости
о виде распределения генеральной
совокупности для уровня значимости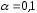 .
Сделать статистический вывод.
.
Сделать статистический вывод.Построить доверительные интервалы для неизвестных математического ожидания и дисперсии нормально распределенной генеральной совокупности с параметрами
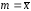 и
и для уровней значимости
для уровней значимости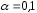 ,
,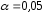 и
и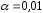 .
Сделать вывод о ширине доверительного
интервала, в зависимости от уровня
значимости
.
Сделать вывод о ширине доверительного
интервала, в зависимости от уровня
значимости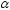 .
.
У к а з а н и е:все вычисления проводить с точностью до 0,0001
ГЕНРАЛЬНАЯ СОВОКУПНОСТЬ И ВЫБОРКА
В математической статистике рассматриваются случайные эксперименты, которые состоят в проведении nповторных независимых наблюдений над некоторой случайной величинойX, имеющей неизвестное распределение вероятностей.
Генеральной совокупностьюназывают множество всех возможных значений случайной величиныX, наблюдаемой в эксперименте .
Выборкойназывают часть генеральной
совокупности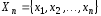 ,
то есть конечное подмножество значений
случайной величины из множества элементов
генеральной совокупности.
,
то есть конечное подмножество значений
случайной величины из множества элементов
генеральной совокупности.
Объемомвыборки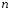 называют количество содержащихся в ней
значений случайной величины
называют количество содержащихся в ней
значений случайной величины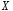 .
.
Задачаматематической статистики состоит в исследовании свойств выборки и обобщении этих свойств на всю генеральную совокупность.
Выборка является исходной информацией
для статистического анализа и принятия
решений о неизвестных вероятностных
характеристиках случайной величины
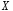 .
Для этих целей на выборку следует
смотреть как на набор реализаций
.
Для этих целей на выборку следует
смотреть как на набор реализаций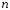 независимых одинаково распределенных
случайных величин
независимых одинаково распределенных
случайных величин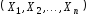 .
.
Для того чтобы по выборке можно было достаточно уверенно судить о генеральной совокупности, выборка должна быть представительной(репрезентативной),то есть достаточно полно представлять признаки и параметры генеральной совокупности. Репрезентативность выборки улучшается при увеличении её объема.
ТОЧЕЧНЫЕ ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
Пусть
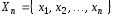 – выборка объема
– выборка объема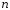 из генеральной совокупности значений
случайной величины
из генеральной совокупности значений
случайной величины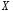 с математическим ожиданием
с математическим ожиданием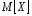 ,
дисперсией
,
дисперсией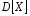 и среднеквадратическим отклонением
и среднеквадратическим отклонением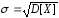 .
.
Выборочным среднимвыборки называется среднее арифметическое
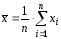 .
.
Согласно закону больших чисел, при увеличении объема выборки среднее арифметическое выборки сходится по вероятности к математическому ожиданию генеральной совокупности, то есть
 .
.
Таким образом, среднее арифметическое может служить приближением (оценкой) математического ожидания генеральной совокупности.
Выборочной дисперсиейназывается
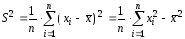 .
.
Модифицированной выборочной дисперсией называется
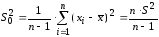 .
.
Все эти выборочные величины зависят от выборки и сами являются случайными величинами. Их значения лишь приближенно равны соответствующим числовым характеристикам генеральной совокупности.
Статистикойназывается любая
функция, зависящая от выборки и сама
являющаяся случайной величиной. Таким
образом, выборочное среднее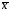 ,
выборочная дисперсия
,
выборочная дисперсия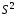 и модифицированная выборочная дисперсия
и модифицированная выборочная дисперсия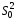 – это статистики.
– это статистики.
Точечной оценкой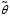 неизвестного параметра
неизвестного параметра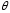 распределения случайной величины
распределения случайной величины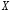 называется такая функция от выборки
(статистика)
называется такая функция от выборки
(статистика)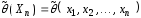 ,
что ее значение от любой выборки
приближенно равно истинному значению
параметра, то есть
,
что ее значение от любой выборки
приближенно равно истинному значению
параметра, то есть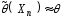 .
.
Оценки параметров принято обозначать
символом с тильдой наверху:
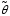 .
.
Существует несколько методов нахождения точечных оценок: метод наименьших квадратов, метод моментов, метод максимального правдоподобия и другие. Таким образом, для каждого независимого параметра может быть несколько оценок, полученных различными методами. Для того, чтобы точечная оценка давала хорошее приближение оцениваемому параметру, она должна обладать следующими свойствами:
Оценка
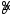 параметра называетсянесмещенной,
если ее математическое ожидание равно
оцениваемому параметру
параметра называетсянесмещенной,
если ее математическое ожидание равно
оцениваемому параметру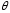 :
:
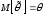 .
.
Известно, что
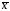 – несмещенная оценка математического
ожидания,
– несмещенная оценка математического
ожидания,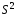 – смещенная оценка дисперсии и
– смещенная оценка дисперсии и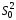 – несмещенная оценка дисперсии.
– несмещенная оценка дисперсии.
Оценка
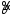 параметра называетсясостоятельной,
если она сходится по вероятности к
точному значению оцениваемого параметра
параметра называетсясостоятельной,
если она сходится по вероятности к
точному значению оцениваемого параметра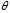 ,
то есть
,
то есть
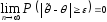
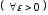 .
.
Состоятельной оценкой математического
ожидания является выборочное среднее
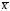 ,
а состоятельными оценками дисперсии –
выборочная дисперсия
,
а состоятельными оценками дисперсии –
выборочная дисперсия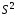 и модифицированная выборочная дисперсия
и модифицированная выборочная дисперсия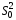 .
.
Несмещенная оценка
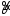 параметра называетсяэффективной,
если она имеет минимальную дисперсию
среди всех несмещенных оценок этого
параметра. Доказано, что
параметра называетсяэффективной,
если она имеет минимальную дисперсию
среди всех несмещенных оценок этого
параметра. Доказано, что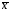 и
и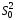 являются эффективными оценками
математического ожидания и дисперсии
соответственно, а так как
являются эффективными оценками
математического ожидания и дисперсии
соответственно, а так как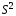 – смещенная оценка дисперсии, то это
и неэффективная оценка.
– смещенная оценка дисперсии, то это
и неэффективная оценка.
ПРИМЕР 1
Дана выборка значений случайной величины
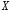 (выборка объема
(выборка объема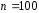 из генеральной совокупности)
из генеральной совокупности)
Таблица 1
|
-7,53 |
-3,42 |
-2,09 |
-1,09 |
|
-5,59 |
-3,28 |
-2,03 |
-1,00 |
|
-5,52 |
-3,23 |
-2,03 |
-0,93 |
|
-5,41 |
-3,23 |
-2,00 |
-0,86 |
|
-5,19 |
-3,22 |
-1,95 |
-0,79 |
|
-4,97 |
-3,14 |
-1,94 |
-0,74 |
|
-4,76 |
-3,12 |
-1,91 |
-0,70 |
|
-4,54 |
-3,09 |
-1,90 |
-0,49 |
|
-4,52 |
-2,92 |
-1,88 |
-0,35 |
|
-4,44 |
-2,88 |
-1,88 |
-0,28 |
|
-4,42 |
-2,84 |
-1,87 |
-0,21 |
|
-4,38 |
-2,82 |
-1,78 |
-0,19 |
|
-4,34 |
-2,77 |
-1,77 |
-0,16 |
|
-4,28 |
-2,69 |
-1,74 |
-0,04 |
|
-4,26 |
-2,65 |
-1,56 |
0,15 |
|
-4,17 |
-2,64 |
-1,53 |
0,16 |
|
-4,13 |
-2,60 |
-1,45 |
0,24 |
|
-3,96 |
-2,58 |
-1,41 |
0,27 |
|
-3,93 |
-2,55 |
-1,33 |
0,35 |
|
-3,90 |
-2,51 |
-1,30 |
0,37 |
|
-3,83 |
-2,41 |
-1,26 |
0,41 |
|
-3,70 |
-2,38 |
-1,23 |
0,53 |
|
-3,63 |
-2,34 |
-1,19 |
0,65 |
|
-3,62 |
-2,31 |
-1,16 |
0,79 |
|
-3,46 |
-2,29 |
-1,09 |
1,36 |
Требуется найти выборочные оценки
математического ожидания, дисперсии и
среднеквадратического отклонения
случайной величины
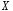 .
Указать свойства этих оценок.
.
Указать свойства этих оценок.
Оценкой математического ожидания
случайной величины
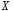 служит выборочное среднее
служит выборочное среднее
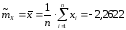 .
.
Данная оценка
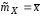 является несмещенной, эффективной и
состоятельной.
является несмещенной, эффективной и
состоятельной.
Оценкой дисперсии случайной величины
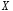 служат выборочная дисперсия и
модифицированная выборочная дисперсия,
вычисляемые по формулам:
служат выборочная дисперсия и
модифицированная выборочная дисперсия,
вычисляемые по формулам:
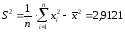
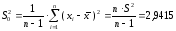 .
.
Оценка
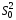 является несмещенной, эффективной,
состоятельной, а
является несмещенной, эффективной,
состоятельной, а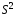 – смещенная, неэффективная, но
состоятельная. Следовательно,
– смещенная, неэффективная, но
состоятельная. Следовательно,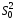 дает лучшее приближение оцениваемой
дисперсии, поэтому в дальнейших расчетах
в качестве оценки дисперсии используется
дает лучшее приближение оцениваемой
дисперсии, поэтому в дальнейших расчетах
в качестве оценки дисперсии используется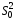 :
: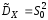 .
.
Оценка среднеквадратического отклонения, являющаяся несмещенной, эффективной, состоятельной:
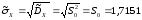 .
.
