19.Примеры практического применения

Определение корреляционных функций детерминированных сигналов

Найдем автокорреляционную функцию K(τ) одиночного прямоугольного импульса амплитуды A и длительностью τ_и. Вычислим коэффициент корреляции r(τ) и интервал корреляции.

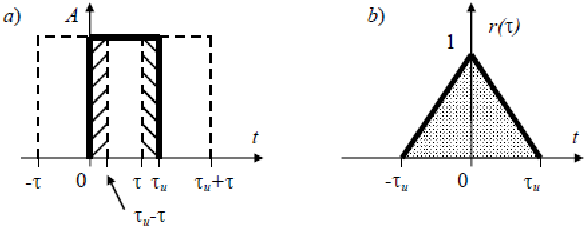
Рис. 3.8. Нахождение функции автокорреляции. a) – исходный импульс, b) – график коэффициента корреляции (жирной линией показано исходное положение импульса, а пунктиром – копии импульса, сдвинутые на интервал τ влево и вправо относительно исходного положения)

Из рисунка 3.8 видно, что перекрытие импульсов имеет место при 0<t<τи.

Следовательно, автокорреляционная функция K(τ) отлична от нуля на интервалах [0, τи-τ] и [τ, τи]. Переменный сдвиг τ соответствует только положительным значениям, следовательно, при подстановке его в пределы интегрирования нужно использовать абсолютное значение |τ| :

При τ = 0 значение функции автокорреляции K(0)=A2τи.

Коэффициент корреляции

Свертка

Измеренная интенсивность выражается через интенсивность спекл-картины как свертка с функцией, описывающей форму приемной апертуры

Рассмотрим достаточно распространенный случай – дифракция на объекте типа щелевое отверстие. Распределение интенсивности в плоскости фотоприемника

Световой поток, падающий на фотоприемник в каждый момент времени, с точностью до постоянного множителя

где x0 – координата середины сканирующей щелевой диафрагмы; b – ширина щели; b = kπ (см. рис. 3.9).

Рис. 3.9. Схема расчета влияния полевой диафрагмы

Преобразуя последнее выражение, получим

где Si – интегральный синус.

Анализ данного выражения показывает, что с увеличением отношения b/π величина светового потока растет и, следовательно, растет амплитуда электрического сигнала. Контраст ДК при этом уменьшается (рис. 3.10). Форма кривой при этом также изменяется, что может привести к изменению расстояния между точками с минимальной интенсивностью, несущих информацию о размере объекта.

Рис. 3.10. Влияние ширины щели фотоприемника на контраст ДК

Измеренное и истинное значения контрастности. Рассмотрим случай считывания интерференционной картины с помощью фотоприемника с конечным размером чувствительной площадки (перед фотоприемником установлена щелевая диафрагма).

Рис. 3.11. К расчету интенсивности света, прошедшего через щель шириной b

Распределение интенсивности в интерференционной картине можно описать функцией cos2 (πx / b) , где b - ширина щелевой диафрагмы, а ϖ - ширина интерференционного максимума, x – текущая координата.

Такая запись аргумента функции позволяет выразить результат расчета в относительных величинах, что удобно для последующего анализа.

Функцию косинус квадрат выразим через косинус двойного угла

В этом случае вычисление интеграла упрощается.

Энергия света, проходящего через щель шириной ϖ, пропорциональна заштрихованной на рис. области

где x0 – координата середины щели. Интегрирование дает

При перемещении щели или полос по полю максимальное и минимальное значения энергии:

Отсюда измеренная контрастность полос

20. Радиус корреляции лазерного излучения

Модуль степени пространственной когерентности является квазипериодической функцией. В реальных случаях база резонатора L много больше характерного размера зеркал a (L >> a), а число Френеля (ka²/ 2πL) ≥1.

С учетом этого условия, радиус корреляции r_k≈ a / N_⊥.

Приближенный расчет радиуса корреляции лазерного поля со статистически независимыми модами можно выполнить и другим способом - оценивая средний размер неоднородности по возбуждаемым модам, который в соответствии с выражением для распределения амплитуды моды по половинному уровню можно оценить как rm ≈ 2a ⁄ m.

Для плоского резонатора получим r_k≈ 2a ln N_⊥/N_⊥.

Аналогичным способом, исходя из масштаба радиальных неоднородностей можно найти радиус корреляции для сферического резонатора

Зависимость радиуса поперечной корреляции от формы резонатора

Зависимость радиуса корреляции от числа поперечных мод хорошо подтверждается экспериментально. С увеличением числа поперечных мод вид функции когерентности стремится к виду функции когерентности для некогерентного источника, что согласуется с теоремой Ван Циттерта-Цернике.

Вид экспериментальной поперечной корреляционной функции излучения твердотельного многомодового лазера. N – число мод

Радиус корреляции лазерного пучка, как и ширина пучка, является функцией продольной координаты z.