
- •Спрос, предложение, рыночная цена
- •Что такое предложение?
- •Равновесная цена
- •Рыночный механизм спроса и предложения
- •Эластичность и ее применение
- •Эластичность спроса
- •Эластичность спроса по цене и ее детерминанты
- •Расчет эластичности спроса по цене
- •Виды кривых спроса
- •Узелок на память
- •Совокупная выручка и ценовая эластичность спроса
- •Эластичность спроса по доходу
- •Эластичность предложения
- •Эластичность предложения по цене и определяющие ее факторы
- •Узелок на память
- •Расчет эластичности предложения по цене
- •Виды кривых предложения
- •Три примера практического применения спроса и эластичности
- •Могут ли новости об увеличении урожайности ввергнуть фермеров в тревогу?
- •Почему орес не удалось сохранить высокие цены на нефть?
- •Заключение
- •Кривые безразличия и их свойства
- •Закон убывающей предельной производительности
- •Классификация издержек (затрат) производства
- •60. Правила максимизации прибыли
- •Монополия и монопольная власть
- •[Edit] Что дает монопольную власть?
- •[Edit] Барьеры входа
- •[Edit] Прибыль монополии
- •[Edit] Рассчетный пример
- •[Edit] Монопольная власть и ее оценка
- •[Edit] Измерение монопольной власти
- •[Edit] Показатель монопольной власти Лернера
- •[Edit] Индекс монопольной власти
- •[Edit] Индекс Херфиндаля - Хиршмана
- •Микроэкономика: Рынок труда. Индивидуальная кривая предложения труда.
- •Проблема безработицы и способы борьбы с ней
- •Валовой внутренний продукт (ввп) и валовой национальный продукт (внп)
- •1. Определение.
- •4. Тест.
- •Реальный ввп России, млрд. Долларов сша
- •Совокупный спрос. Ценовые и неценовые факторы совокупного спроса
- •Совокупное предложение. Кривая совокупного предложения: кейнсианский, классический и промежуточный отрезки. Неценовые факторы совокупного предложения
- •Часть 1
- •Часть 1
- •Часть 1
- •Сальдо государственного бюджета
- •Способы финансирования дефицита государственного бюджета
- •Государственный долг, его виды и последствия
- •1. Инфляция спроса
- •2. Инфляция предложения (издержек)
Кривые безразличия и их свойства
Предположим, что потребитель имеет набор благ, состоящий из X и Y. Все соотношения количеств этих благ для него равноценны, потребителю безразлично, какой набор выбрать. Следовательно, эти товары принадлежат к набору безразличия. Набор безразличия— набор вариантов потребительского выбора, каждый из которых обладает одинаковой полезностью и поэтому не имеет предпочтения перед другими.
Кривая безразличия является графическим отображением набора безразличия. Кривая безразличия— совокупность наборов благ, обеспечивающих потребителю равный объем удовлетворения потребностей, т. е. приносящих ему одинаковую полезность. Взяв другие возможные сочетания благ, соответствующие различным величинам совокупной полезности, можно составить карту безразличия.Карта безразличия— совокупность кривых безразличия, соответствующих различным уровням полезности для одного потребителя и одной пары благ. Вкусы и предпочтения потребителя представляются картой кривых безразличия. Каждая следующая кривая безразличия, проходящая дальше от начала координат, предполагает относительно большую величину полезности.


Любая кривая безразличия представляет одинаковую совокупную полезность различных благ для потребителя. Кривая безразличия (U) состоит из точек, символизирующих наборы товаров Х и Y. Совокупные полезности всех наборов, представленные точками на этой кривой одинаковы, т. е. потребителю безразлично, какую именно комбинацию товаров Х и Y он приобретет. Переходя от точки А к точке В, потребитель сокращает потребление блага Y на ΔY и наращивает потребление товара X наΔХ, но общий уровень удовлетворения потребителя (совокупная полезность) остается неизменным (рисунок ниже).

Зона замещения (субституции)— участок кривой безразличия, на котором возможна эффективная замена одного блага другим.
Взаимная замена благ X и Y возможна только в пределах отрезка АВ (зоне замены). Количество блага Х1представляет минимально необходимое количество потребления блага X, от которого потребитель не может отказаться, как бы много товара Y ни предлагалось взамен. Аналогично Y1— минимально необходимое количество потребления блага Y. Предельная норма замещения — норма, в соответствии с которой одно благо может быть заменено другим благом без выигрыша или потери полезности для потребителя. Предельная норма замещения — количество одного блага, от которого потребитель готов отказаться, чтобы получить дополнительную единицу другого блага. Предельная норма замещения рассчитывается следующим образом:

где MRS — предельная норма замещения; Qx— количество товара X; QY— количество товара Y.
Предельная норма замещения всегда отрицательная величина, так как прирост потребления одного блага происходит за счет сокращения потребления другого. Предельная норма замещения уменьшается при движении вдоль кривой безразличия — получая в свое распоряжение все большее количество данного блага и наращивая его потребление, покупатель в обмен готов отказаться от все меньшего количества другого блага, которое становится все более дефицитным. У потребителя, желающего остаться на той же кривой безразличия, прирост полезности от наращивания потребления блага X должен быть равен потере полезности от сокращения потребления товара Y. Таким образом, предельная норма замещения блага X благом Y может рассматриваться как отношение предельной полезности блага X к предельной полезности блага Y:

Рассмотрим некоторые свойства кривых безразличия:
• кривые безразличия имеют отрицательный наклон. Между количествами благ X и Y существует обратная связь. При уменьшении потребления одного блага, для компенсации потерь и сохранения прежнего уровня полезности, потребитель должен увеличить потребление другого блага. Любая кривая, выражающая обратную связь переменных, имеет отрицательный наклон;
• кривые безразличия выпуклы по отношению к началу координат. Выше отмечалось, что при увеличении потребления одного блага потребитель должен уменьшить потребление другого блага. Выпуклость кривой безразличия по отношению к началу координат является следствием падения предельной нормы замещения. Пологий спуск кривой безразличия вниз или подъем наверх свидетельствует об убывании темпов замещения одного блага другим по мере уменьшения доли данного блага в потребительской корзине;
• абсолютная величина наклона кривой безразличия равна предельной норме замещения. Угол наклона кривой безразличия в данной точке показывает норму, в соответствии с которой одно благо может быть заменено другим благом без выигрыша или потери полезности для потребителя. Данное соотношение характеризуется предельной нормой замещения;
• кривые безразличия не пересекаются. Один и тот же потребитель не может характеризовать один и тот же набор благ различными уровнями полезности. Следовательно, две кривые безразличия, представляющие различные уровни полезности, не могут пересечься;
• возможно построить кривую безразличия, проходящую через любой набор благ. Кривую безразличия можно построить для любой пары благ, приносящих определенный уровень полезности. Именно по этому принципу строится карта безразличия, дающая полную информацию о системе предпочтений потребителя.
8
БЮДЖЕТНАЯ ЛИНИЯ. ОПТИМУМ ПОТРЕБИТЕЛЯ
Карта безразличия представляет собой графическое отображение системы предпочтений потребителя. Естественно, потребитель стремится приобрести товарный набор, принадлежащий наиболее удаленной от начала координат кривой безразличия. Но он ограничен в своих средствах. Далеко не всякий товарный набор ему доступен. Для изображения множества доступных потребителю товарных наборов используется бюджетная линия.
Обозначим месячный доход потребителя через I. Для упрощения предположим, что потребитель не делает никаких сбережений и весь свой доход расходует на приобретение только двух товаров X и Y. Бюджетное ограничение потребителя можно записать в форме следующего равенства:
I = PXX + PYY (3.10)
Бюджетное ограничение имеет очевидный смысл: доход потребителя равен сумме его расходов на покупку товаров X и У. Преобразуем равенство (3.10) к следующему виду:
Y= I/РXХ +I/ PYY (3.11).
Мы получили уравнение бюджетной линии, или, как ее еще называют, линии цен. На рис. 3.8 эта линия первоначально занимает положение KL.
Точки пересечения бюджетной линии с осями координат можно получить следующим образом. Если потребитель весь свой доход / израсходует только на покупку товара X, то он сможет приобрести I/PX единиц этого товара. Поэтому длина отрезка OL равна I/PX. Аналогично можно показать, что длина отрезка ОК равна 1/РY. Наклон бюджетной линии равен ≈РX/РY ≈ коэффициенту при X в уравнении (3.11).
Все товарные наборы, соответствующие точкам на бюджетной линии, стоят ровно / руб. и являются потому доступными для нашего потребителя. Все товарные наборы, расположенные выше и правее бюджетной линии, стоят более I руб. и недоступны для потребителя. Таким образом, бюджетная линия ограничивает сверху множество доступных для потребителя товарных наборов.
Как изменится положение бюджетной линии при изменении дохода потребителя и цен на товары? Допустим сначала, что доход потребителя уменьшается до I▓ < I, цены на товары при этом остаются неизменными. Наклон бюджетной линии не изменится, поскольку он определяется только соотношением цен. Следовательно, произойдет параллельный сдвиг бюджетной линии вниз. Она займет положение К'L'. При увеличении дохода и неизменных ценах будет наблюдаться параллельный сдвиг бюджетной линии вверх. Предположим теперь, что доход и цена товара X неизменны, цена же товара Y понизилась до Р▓Y < РY. Очевидно, что в этом случае точка L не изменит своего положения, поскольку оно определяется неизменными I и РX. Левый же конец бюджетной линии сдвинется вверх и займет положение К". Читатель может без труда определить, что случится с бюджетной линией при повышении РY, повышении или понижении РX.
Совместим теперь на рис. 3.9 карту безразличия нашего потребителя с его бюджетной линией KL.

Какой товарный набор выберет потребитель? Из всех доступных для него наборов потребитель выберет тот, который принадлежит наиболее удаленной от начала координат кривой безразличия. Именно этот набор обеспечит ему максимум удовлетворения. Потребитель не выберет точку А, в которой бюджетная линия пересекает некоторую кривую безразличия, ведь при движении вдоль бюджетной линии вправо вниз потребитель может перейти к товарным наборам, лежащим на более удаленных от начала координат кривых безразличия. По аналогичным причинам потребитель не выберет точку В. Он выберет точку Е, в которой бюджетная линия лишь касается некоторой кривой безразличия U2. Оптимальный для потребителя товарный набор Е содержит XE единиц товара X и YE единиц товара Y.
В точке Е наклоны бюджетной линии и кривой безразличия совпадают. Напомним, что наклон бюджетной линии равен ≈РX/РY, наклон кривой безразличия равен ≈MRSXY. Поэтому в точке оптимума выполняется равенство
РX/РY = MRSXY (3.12)
Условие оптимума потребителя (3.12) можно интерпретировать следующим образом. Соотношение, в котором потребитель при данных ценах способен замещать один товар другим, равно соотношению, в котором потребитель согласен замещать один товар другим без изменения уровня своего удовлетворения.
Равенство (3.12) в порядковой теории полезности имеет такой же смысл, что и равенство (3.4) в количественной теории. Действительно, согласно (3.8),
MRSXY = MUX/MUY
Подставив (3.8) в (3.12), получаем условие оптимума потребителя в следующем виде:
РX/РY = MUX/MUY или MUX/РX = MUY/РY (3.13)
Последнее равенство совпадает с равенством (3.4).
Оптимальное решение, представленное на рис. 3.9, называют часто внутренним, поскольку точка Е лежит "внутри" двумерного пространства товаров, точнее ≈ его I квадранта. Однако в некоторых ситуациях бюджетная прямая и кривая безразличия имеют разный наклон на всем их протяжении и, значит, точки касания их вообще не существует. В этом случае оптимальное решение определяется положением, наиболее близким к касанию, и называется угловым. Оно определяется пересечением бюджетной прямой, одной из осей координат и кривой безразличия.
На рис. 3.10 бюджетная прямая KL ограничена точками К, где X = 0, и L, где Y = 0. Оптимум потребителя достигается либо в точке К (рис. 3.10,о), если
MRSXY ≤ РX/РY
либо в точке L (рис. 3.10,б), если
MRSXY ≥ РX/РY
В первом случае наклон кривой безразличия в точке К меньше или равен наклону бюджетной прямой, во втором наклон кривой безразличия в точке L больше или равен наклону бюджетной прямой.
Из всех доступных потребителю наборов набор К (рис. 3.10,а) и набор L (рис. 3.10,6) лежат на наиболее удаленных от начала координат кривых безразличия. Набор К не содержит товара X, набор L ≈ товара Y. Естественно, для точек К и L условие (3.12) может и не выполняться. Угловое решение в порядковой теории полезности соответствует условию (3.5) в количественной теории.
9, 11 косты и кванты
Изокванта
|
|
|
|
Для простоты анализа, как и прежде, будем полагать, что:
исследуемая функция производства зависит от двух факторов: труда и капитала и является частным случаем функции Кобба-Дугласа и имеет вид
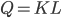
факторы производства в определенных пределах будут взаимозаменяемыми
технология производства в течение всего рассматриваемого периода не меняется
Представим
в виде таблицы данную функцию для
значений
![]() и
и![]() от
1 до 4.
от
1 до 4.
|
|
1 |
2 |
3 |
4 |
|
1 |
1 |
2 |
3 |
4 |
|
2 |
2 |
4 |
6 |
8 |
|
3 |
3 |
6 |
9 |
12 |
|
4 |
4 |
8 |
12 |
16 |
Как
видно из таблицы, существует несколько
комбинаций труда
и капитала,
обеспечивающих в определенных пределах
заданный объем выпуска. Например
![]() можно
получить, используя комбинацию (1,4),
(4,1) и (2,2).
можно
получить, используя комбинацию (1,4),
(4,1) и (2,2).
Если отложить по горизонтальной оси количество единиц труда, а по вертикальной — количество единиц капитала, затем обозначить точки, в которых фирма выпускает один и тот же объем, то получится кривая, представленная на рисунке 14.1 и называемая изоквантой.
Каждая точка изокванты соответствует комбинации ресурсов, при которой фирма выпускает заданный объем продукции.
Набор изоквант, характеризующий данную производственную функцию, называется картой изоквант.

Свойства изоквант
Свойства стандартных изоквант аналогичны характеристикам кривых безразличия:
Изокванта, так же как и кривая безразличия, является непрерывной функцией, а не набором дискретных точек.
Для любого заданного объема выпуска может быть проведена своя изокванта, отражающая различные комбинации экономических ресурсов, обеспечивающих производителю одинаковый объем производства (изокванты, описывающие данную производственную функцию, никогда не пересекаются).
Изокванты не имеют участков возрастания (Если бы участок возрастания существовал, то при движении вдоль него увеличивалось бы количество как первого, так и второго ресурса).
Предельная норма технологического замещения
Предельная норма технологического замещения одного ресурса на другой (например, труда на капитал) показывает степень замещения труда капиталом, при котором объем выпуска остается неизменным.
Алгебраическое
выражение, показывающее степень, в
которой производитель готов сократить
количество капитала в обмен на увеличение
труда, достаточную для сохранения
прежнего объема выпуска имеет вид:
![]() .
.

Как
видно на рисунке выше, при переходе из
точки
![]() в
точку
в
точку![]() объем
производства остается неизменным. Это
означает что сокращение выпуска в
результате уменьшения затрат капитала
объем
производства остается неизменным. Это
означает что сокращение выпуска в
результате уменьшения затрат капитала![]() компенсируется
увеличением выпуска за счет использования
дополнительного количества труда
компенсируется
увеличением выпуска за счет использования
дополнительного количества труда![]() .
.
Сокращение
выпуска в результате уменьшения затрат
капитала равно произведению
![]() на
предельный продукт капитала, или
на
предельный продукт капитала, или![]() .
Увеличение выпуска за счет использования
дополнительного количества труда в
свою очередь равно произведению
.
Увеличение выпуска за счет использования
дополнительного количества труда в
свою очередь равно произведению![]() на
предельный продукт труда, или
на
предельный продукт труда, или![]() .
.
Таким
образом, можно записать, что
![]() .
Запишем данное выражение по-иному:
.
Запишем данное выражение по-иному:![]() или
или![]() .
.
Производственная
функция, связывающая между собой
количество капитала, труда и объем
выпуска, позволяет также рассчитать
предельную норму технологического
замещения через производную данной
функции:
![]() .
.
Это значит, что графически в любой точке изокванты предельная степень технологического замещения равна тангенсу угла наклона касательной к изокванте в этой точке.
Пример 14.2 Нахождение MRTS для заданной функции
Условие:
Пусть производственная функция имеет
вид
![]() .
.
Определить:
![]() при
при![]() для
для![]() .
.
Решение:
![]() ,
,
![]()
![]()
Очевидно, что степень замещения труда капиталом не остается постоянной при движении вдоль изокванты. При перемещении вниз по кривой абсолютное значение MRTS труда капиталом убывает, так как все большее количество труда приходится использовать, чтобы компенсировать снижение затрат капитала (Так, в приведенном выше примере при L=1 MRTS=-10, а при L=10 MRTS=-0.1.)
В дальнейшем MRTS достигает своего предела (MRTS=0), а изокванта приобретает горизонтальный вид. Очевидно, что дальнейшее снижение затрат капитала приведет лишь к сокращению объемов выпуска. Количество капитала в точке Е — минимально допустимое для данного объема производства (аналогичным образом минимально допустимое для производства данного объема количество труда имеет место в точке А).

Убывание предельной нормы технологического замещения
Убывание MRTS одного ресурса другим характерно для большинства производственных процессов и характерно для всех изоквант стандартного вида.
Особые случаи производственной функции (изокванты нестандартного вида)
Совершенная взаимозаменяемость ресурсов
Если
ресурсы, используемые в процессе
производства, являются абсолютно
заменяемыми, то
![]() постоянна
во всех точках изокванты, а карта изоквант
имеет вид как на рисунке 14.2. (Примером
такого производства может служить
производство, допускающее как полную
автоматизацию, так и ручное изготовление
какого-либо продукта).
постоянна
во всех точках изокванты, а карта изоквант
имеет вид как на рисунке 14.2. (Примером
такого производства может служить
производство, допускающее как полную
автоматизацию, так и ручное изготовление
какого-либо продукта).

Фиксированная структура использования ресурсов
Если
технологический процесс исключает
замещение одного фактора на другой и
требует использование обоих ресурсов
в строго фиксированных пропорциях,
производственная функция имеет вид
латинской буквы
![]() ,
как на рисунке 14.3.
,
как на рисунке 14.3.

Примером подобного рода может служить работа землекопа (одна лопата и один человек). Увеличение одного из факторов без соответствуюещго изменения количества другого фактора нерационально, поэтому технически эффективными будут лишь угловые комбинации ресурсов (угловая точка — точка, где пересекаются соответствующие горизонтальная и вертикальная линии).
Изокоста
Как мы уже выяснили раньше, набор изоквант отдельной фирмы (карта изоквант) показывают технически возможные комбинации ресурсов, обеспечивающие фирме соответствующие объемы выпуска. Однако при выборе оптимальной комбинации ресурсов производитель должен учитывать не только доступную ему технологию, но и свои финансовые ресурсы, а также цены на соответствующие факторы производства.
Совокупность двух последних факторов определяет область доступных производителю экономических ресурсов.
Бюджетное ограничение производителя может быть записано в виде неравенства:
![]()
где:
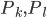 цена
капитала и труда
цена
капитала и труда —количество
капитала и труда
—количество
капитала и труда —совокупные
расходы (издержки)
фирмы на приобретение ресурсов
—совокупные
расходы (издержки)
фирмы на приобретение ресурсов
Если производитель полностью расходует свои средства на приобретение данных ресурсов, то мы получаем равенство:
![]() или
или
![]()
Полученное уравнение называют уравнением изокосты.

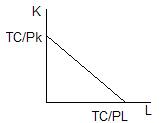
Линия изокосты представленная на рисунке 14.4 показывает набор комбинаций экономических ресурсов (в данном случае труда и капитала), которые фирма может приобрести с учетом рыночных цен на ресурсы и при полном использовании своего бюджета.
Наклон линии изокосты определяется отношением рыночных цен на труд и на капитал ( — РL/РK), что вытекает из уравнения изокосты.
Линия изокосты производителя
Оптимальная комбинация ресурсов
Стремление фирмы к эффективному производству побуждает ее к достижению максимально возможной выработки при заданных затратах на ресурсы, или, что же самое, к минимизации издержек при производстве заданного объема выпуска.
Комбинация ресурсов, обеспечивающая минимальный уровень совокупных издержек фирмы, называется оптимальной и лежит в точке касания линий изокосты и изокванты.

Соединив изокваты и изокосты, можно определить оптимальную позицию фирмы. Точка, в которой изокванта касается изокосты, означает наиболее дешевую по стоимости комбинацию факторов, необходимых для выпуска определенного объема продукции.
Американские экономисты Дуглас и Солоу выявили, что увеличение затрат труда на 1% обеспечивает 3/4 прироста выпущенной продукции, а увеличение затрат капитала на 1% дает возможность увеличить на 1/4 количество выпущенной продукции.
Эти индексы (3/4 и 1/4) были названы агрегатными, а зависимость между выпуском продукции и факторами производства вошла в жизнь под названием агрегатной функции производства. которая позволяет утверждать, что вложения в человеческий капитал, дают больший эффект в увеличении производства, чем рост средств производства.
Траектория развития
Совокупность
точек оптимума производителя, построенных
для изменяющегося объема производства,
и, следовательно, меняющихся затрат (![]() )
фирмы при неизменности цен на ресурсы,
отражает траекторию развития фирмы.
Рисунок 14.6.
)
фирмы при неизменности цен на ресурсы,
отражает траекторию развития фирмы.
Рисунок 14.6.

Форма траектории развития рассматривается обычно в долгосрочном периоде и позволяет выделить капиталоемкие (рисунок 14.7а), трудоемкие (рисунок 14.7б) способы производства, а также технологии, предполагающие равномерное увеличение использования как труда, так и капитала (рисунок 14.7в).

10
