8. Операции над матрицами и их свойства. Доказать одно из них.

Число элементов в строке называется длиной строки.

Определение: Две матрицы называются равными если их размерности равны и равны элементы, стоящие на соответствующих местах.

Определение: Чтобы умножить матрицу на число или число на матрицу, надо каждый элемент матрицы умножить на это число.

Из этого определения вытекают свойства:

1. А*α=α*А

Матрица все элементы которой равны 0 обозначается О.Ясно что для любой матрицы А из поля Р и для каждых чисел α, β из поля Р имеют место соотношения:

2. 1*А=А

3. 0*А=О α*О=О

4. α(βА)=( α β)А

Определение: Суммой двух матриц А и В одинаковой размерности называется матрица С той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц.

Из этого определения вытекают следующие свойства:

1. А+(В+С)=(А+В)+С – ассоциативность

2. А+В=В+А – коммутативность

3. (α+β)А=αА+ βА – дистрибутивность операции умножения числа на матрицу относительно сложения чисел.

α(А+В)= αА+ αВ – дистрибутивность операции умножения числа на матрицу относительно сложения матриц.

4. 4)А+О=А Матрица (-1)А – называется противоположной матрице А и обозначается «-А».

5. А+(-А)=0 (-α)А=-(αА)

-(А+В)=-А+(-В) -(-А)=А

Определение: Для краткости матрицу А+(-В) записывают А-В и называют эту матрицу разностью матриц А и В.

Определение: Пусть даны две матрицы А и В, причем в первой матрице число столбцов равно числу строк во второй матрице

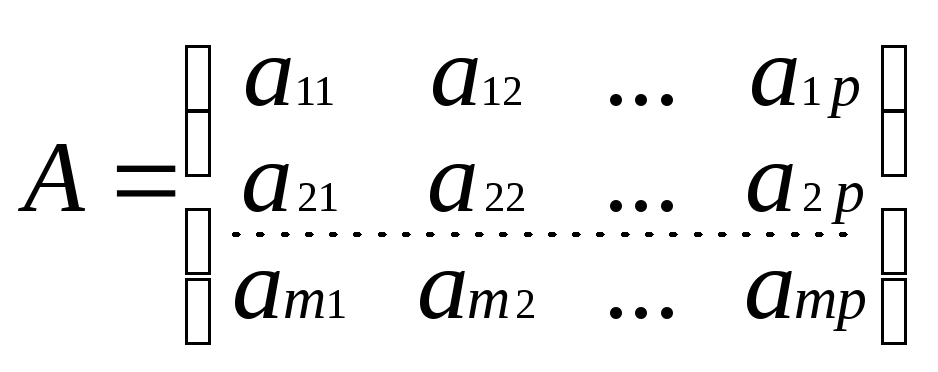
Тогда матрица С=(С_c,j)_m,n, где называется произведением матриц А и В. С=А*В.

Правило умножения матриц можно сформулировать следующим образом:

Чтобы получить элемент стоящий в i-той строке и j-том столбце произведения двух матриц нужно элементы i-той строки первой матрицы умножить на соответствующие элементы j-том столбца второй матрицы и полученные произведения сложить.

Произведение двух матриц некоммутативно, т.е. в общем случае А*В≠В*А

Если рассматривать матрицы не квадратные то может случиться что произведение матриц в одном порядке имеет смысл а в другом не имеет смысла:

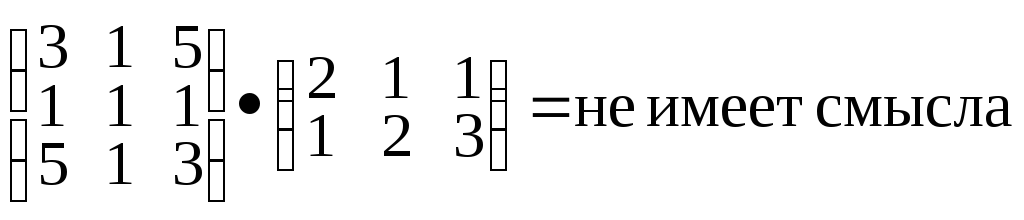
Можно доказать следующие свойства умножения матриц:

1)α(АВ)= (αА)В=А(αВ) Общее значение этих матриц обозначается просто αАВ.

2)(А+В)*С=АС+ВС – дистрибутивность операции умножения матриц справа относительно сложения матриц.

3)С(А+В)=СА+СВ – дистрибутивность операции умножения матриц слева относительно сложения матриц.

Из свойств 2) и 3) следует: Чтобы умножить сумму матриц на сумму матриц нужно каждую матрицу первой суммы умножить на каждую матрицу второй суммы и полученные произведения сложить.

5. А(ВС)=(АВ)С – ассоциативность.

Общее обозначения матриц АВС. Идея всех доказательств доказать что размерности матриц слева и справа равны и что соответствующие элементы матриц равны.

Произведение нескольких матриц А₁,А₂…А_n записанных в определенном порядке от способа расстановки скобок не зависит.

Определение: Квадратная матрица все диагональные элементы которой равны 1 а все недиагональные равны 0, называется единичной матрицей. Обозначается Е.

Непосредственно вычислением устанавливается основное свойство единичной матрицы: АЕ=ЕА=А

Определение: Матрица все элементы которой кроме элементов стоящих на главной диагонали равны 0 называется диагональной матрицей:

Из определения суммы и произведения матриц следует что сумма и произведение диагональных матриц есть диагональные матрицы