32. Смешанное произведение векторов. Определение и основные свойства.

Пусть ,,- какие либо три вектора;- смешанное произведение векторов,,. Следующая теорема позволяет выяснить геометрический смысл смешанного произведения.

Теорема1: Пусть ,,- три некомпланарных вектора.Отложим их от одной точки О. И построим на этих векторах параллелепипед.объему построенного параллелепипеда с + или – в зависимости от того какой является тройка векторов: правой(+) или левой(-).

Отложим от точки О ., гдеS – площадь параллелограмма. , гдеh – высота параллелепипеда, ,,- правая тройка значит +, левая значит - .(ч.т.д.)

Теорема 2: Для того чтобы три вектора ,,были компланарны( линейно зависимы) необходимо и достаточно чтобы(1)

Доказательство: Пусть ,,–компланарны, Если бы эти векторы были не компланарны, тогда на этих векторах можно построить параллелипипед. Объём которого равенV=а,b*c0- а это противоречит (1). Получили противоречие  ,,–компланарны.(ч.т.д.)

Из теорем 1 и 2 следует что т.к. модули и левой и правой частей равны объему одного и того же параллелепипеда и тройки,векторов имеют одинаковую ориентацию. Поэтому в дальнейшем смешанное произведение будем обозначать просто. Смешанное произведение меняет знак при перестановке двух сомножителей нечетное число раз, т.к. каждая перестановка двух сомножителей меняет ориентацию тройки векторов.ому в дальнейшем смешанное произведение будем обозначать просто евой(-).

0000000000000000000000000000000000000000000000000000

Теорема 3: Смешанное произведение векторов выражается через их координаты,,в произвольном базисеследующей формулой:

Доказательство:

(ч.т.д.)

Если базис правый ортонормированный тои тогда

Необходимое и достаточное условие компланарности( линейной зависимости) трех векторов можно теперь записать в координатном виде

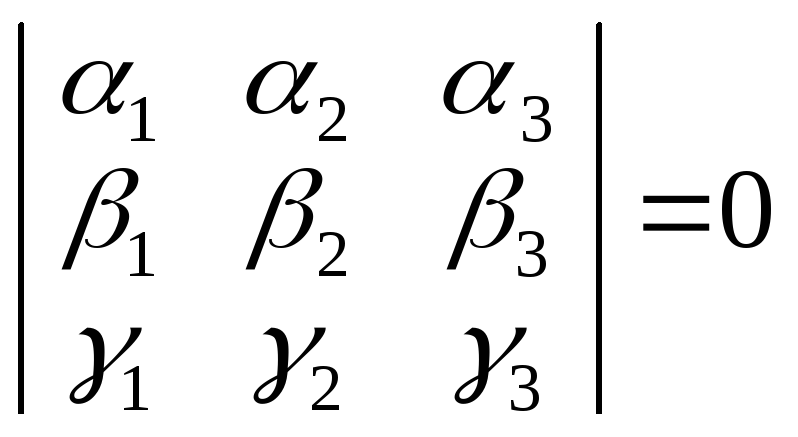
33. Двойное векторное произведение векторов. Определение и формула для вычисления( без доказательства).

Двойным векторным произведением называется произведение .

Можно доказать что для любых трех векторов ,,

34. Алгебраические линии и поверхности. Теоремы об инвариантности( неизменности) порядка.

Определение1: Алгебраической поверхностью называется множество точек, которое в какой-нибудь ДСК может быть задано уравнением вида .- неотрицательные целые числа. Наибольшее из этих чисел называется степенью уравнения или порядком поверхности.

Определение2: Алгебраической линией на плоскости называется множество точек которое в какой-нибудь ДСК на плоскости может быть определено уравнением .называются степенью уравнения или порядком линии.

Теорема об инвариантности( неизменности) порядка: 1. Если поверхность в некоторой ДСК может быть задана уравнением вида (1) то и в любой другой ДСК она может быть задана уравнением того же вида имеющим ту же степень.

2. Если линия на плоскости в некоторой ДСК может быть задана уравнением вида (2) то и в любой другой ДСК она может быть задана уравнением того же вида имеющим туже степень.

Доказательство: Обе теоремы доказываются одинаково. Докажем теорему 2. С этой целью перейдем от ДСК о которой речь шла в определении к произвольной новой ДСК. Новые координаты 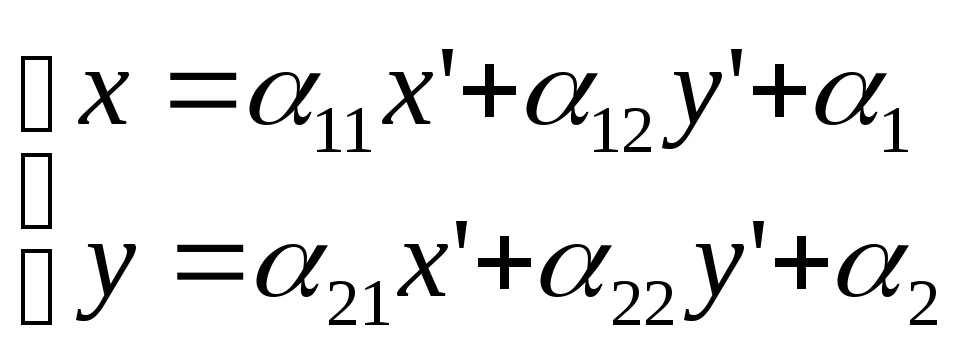. тобы получить новое уравнение линии нужноx и y подставить в (2). Ясно чтопри этом превратится в многочлен в степени (k+e). Степень суммы многочленов не превышает степени старшего члена( степень могла бы понизиться если бы члены с наибольшей степенью взаимно уничтожились). Таким образом мы доказали пока что алгебраическая линия в любой ДСК имеет уравнение вида (2) причем степень уравнения при переходе от одной ДСК к другой не может повыситься. Остается доказать что она не может и понизиться и должна оставаться постоянной. Предположим противное, что при переходе от одной СК к другой степень понизилась, тогда при обратном переходе она должна повыситься что невозможно.(ч.т.д.)