
- •1. .Понятие числового поля и матрицы над полем р.
- •2. Доказать, что любая транспозиция меняет характер четности перестановки. Определение Определителя n-ого порядка.
- •3. Теорема о равноправности строк и столбцов матрицы определителя.
- •4. Теорема о перестановке 2х строк матрицы оределителя. Определитель с двумя одинаковыми строками.
- •5. Теорема об умножении некоторой строки матрицы определителя на одно и то же число. Определитель с двумя пропорциональными строками.
- •6. Теорема о разложении определителя на сумму определителей и следствия из нее.
- •7. Теорема о разложении определителя по элементам строки(столбца) и следствия из неё.
- •8. Операции над матрицами и их свойства. Доказать одно из них.
- •9.Операция транспонирования матрицы и её свойства.
- •10. Определение обратной матрицы. Доказать что у каждой обратимой матрицы существует лишь одно обращение.
- •13. Блочные матрицы. Сложение и умножение блочных матриц. Теорема об определителе квазитреугольной матрицы.
- •14. Теорема об определителе произведения матриц.
- •15. Теорема о существовании обратной матрицы.
- •16.Определение ранга матрицы. Теорема о базисном миноре и следствие из неё.
- •17. Понятие о линейной зависимости строк и столбцов матрицы. Теорема о ранге матрицы.
- •18. Методы вычисления ранга матрицы: метод окаймляющих миноров, метод элементарных преобразований.
- •19. Применение элементарных преобразований только строк(только столбцов) к отысканию обратной матрицы.
- •20. Системы линейных уравнений. Критерий совместности и критерий определенности.
- •21. Решение совместной системы линейных уравнений.
- •22. Однородные системы линейных уравнений. Теорема о существовании фундаментальной системы решений.
- •23. Линейные операции над векторами и их свойства. Доказать одно из них.
- •24. Определение разности двух векторов. Доказать что для любых векторов иразностьсуществует и единственна.
- •25. Определение базиса, координаты вектора в базисе. Теорема о разложении вектора по базису.
- •26. Линейная зависимость векторов. Свойства понятия линейной зависимости, доказать одно из них.
- •28. Декартовы системы координат в пространстве, на плоскости и на прямой. Теорема о линейной комбинации векторов и следствия из нее.
- •29. Вывод формул выражающих координаты точки в одной дск через координаты этой же точки в другой дск.
- •30. Скалярное произведение векторов. Определение и основные свойства.
- •31. Векторное произведение векторов. Определение и основные свойства.
- •32. Смешанное произведение векторов. Определение и основные свойства.
- •33. Двойное векторное произведение векторов. Определение и формула для вычисления( без доказательства).
- •34. Алгебраические линии и поверхности. Теоремы об инвариантности( неизменности) порядка.
- •35. Общие уравнения плоскости и прямой.
- •36. Параметрические уравнения прямой и плоскости.
- •37. Переход от общих уравнений плоскости и прямой на плоскости к их параметрическим уравнениям. Геометрический смысл коэффициентов а,в,с (а,в) в общем уравнении плоскости(прямой на плоскости).
- •38. Исключение параметра из параметрических уравнений на плоскости( в пространстве), канонические уравнения прямой.
- •39. Векторные уравнения прямой и плоскости.
- •40. Общие уравнения прямой в пространстве, приведение к каноническому виду.
- •41. Расстояние от точки до плоскости. Расстояние от точки до прямой. Другие задачи о прямых и плоскостях.
- •42. Определение эллипса. Каноническое уравнение эллипса. Параметрические уравнения эллипса. Эксцентриситет эллипса.
- •44. Определение параболы. Вывод канонического уравнения параболы.
- •45. Кривые второго порядка и их классификация. Основная теорема о квп.
- •45. Поверхности второго порядка и их классификация. Основная теорема о пвп. Поверхности вращения.
- •47.Определение линейного пространства. Примеры.
- •49. Определение Евклидова пространства. Длина вектора. Угол между векторами. Неравенство Коши-Буняковского. Пример.
- •50. Определение евклидова пространства. Теорема Пифагора. Неравенство треугольникаю Пример.
24. Определение разности двух векторов. Доказать что для любых векторов иразностьсуществует и единственна.
Определение: Разностью двух векторов а и b называется такой вектор от прибавления которого к b получается а.
Д ля
того чтобы получить а-b
надо отложить от одной точки а и b,
построить на этих сторонах параллелограмм,
тогда вектор диагональ направленный в
сторону уменьшающегося вектора является
разностью векторов.
ля
того чтобы получить а-b
надо отложить от одной точки а и b,
построить на этих сторонах параллелограмм,
тогда вектор диагональ направленный в
сторону уменьшающегося вектора является
разностью векторов.
Теорема. Для любых векторов а и b, а-b существует и единственно, и выражается формулой а-b=а+(-b)
Доказательство. b+(а+(-b))= b((-b)+a)= (b+(-b))+a=0+a=a
Убедимся теперь в единственности.
Пусть наряду с с=а+(-b) существует d такой что b+d=a
(d+b)+(-b)= d+(b+(-b))=d+0=d
(d+b)+(-b)=a+(-b)=c следовательно с=d (ч.т.д.)
Т.о. a+b=c a=c-b т.е. в векторных равенствах вектора можно переносить из одной части в другую со сменой знака
Определение:
Вектор
е длина
которого равна 1 и имеющий такое же
направление что и ае
называется ортом
![]() .
.
25. Определение базиса, координаты вектора в базисе. Теорема о разложении вектора по базису.
Выражения
вида
![]() называются линейной комбинацией векторов
называются линейной комбинацией векторов![]() .
Числа
.
Числа![]() - коэффициенты линейной комбинации
векторов. Линейная комбинация векторов
обладает следующими свойствами: 1) Если
- коэффициенты линейной комбинации
векторов. Линейная комбинация векторов
обладает следующими свойствами: 1) Если![]() коллинеарны то любая их линейная
комбинация с ними коллинеарна.
коллинеарны то любая их линейная
комбинация с ними коллинеарна.
2)
Если
![]() компланарны то любая их линейная
комбинация с ними компланарна.
компланарны то любая их линейная
комбинация с ними компланарна.
Определение: 1) Любые три некомпланарных вектора взятые в определенном порядке называются базисом в пространстве.
2) Базисом на плоскости называется любая упорядоченная пара не коллинеарных векторов на этой плоскости.
3) Базисом на прямой называется любой отличный от 0 вектор этой прямой.
Вектор базиса на плоскость < >0, а в пространстве никакие 2 вектора не являются коллинеарными.
Если вектор представлен как линейная комбинация некоторых векторов то говорят что этот вектор разложен по этим векторам.
Определение:
Если
![]() базис в пространстве и
базис в пространстве и![]() то числа
то числа![]() называются координатами вектора
называются координатами вектора![]() в базисе
в базисе![]() .
Обозначение
.
Обозначение![]() .
.
![]()
Теорема. (о разложении по базису): 1)Каждый вектор какой-нибудь прямой может быть разложен по базису на этой прямой.
2)Каждый векторнекоторой плоскости может быть разложен по базису на этой плоскости
3)Каждый вектор может быть разложен по базису в пространстве.
4)Координата вектора в каждой из трех случаев определяется однозначно
Доказательство:
1)
Пусть
![]() -
базис на прямой и
-
базис на прямой и![]() .
И пусть
.
И пусть![]() (
+ если
(
+ если![]() и – если
и – если![]() .
Ясно что
.
Ясно что![]() .
.![]() .
.
2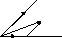 )Пусть
)Пусть
![]() базис на плоскости. Перенесем начала
векторов а, е1
и е2
в точку О. Через конец А вектора а проведем
прямую
базис на плоскости. Перенесем начала
векторов а, е1
и е2
в точку О. Через конец А вектора а проведем
прямую
![]() .
.
Из
рисунка видно что
![]() .
.
3)
Пусть
![]() базис в пространстве. Вектор а –
произвольный.
базис в пространстве. Вектор а –
произвольный.
О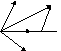 тложим
вектора
тложим
вектора![]() от некоторой точки О. Дальше все
рассуждения аналогичны пункту 2).
от некоторой точки О. Дальше все
рассуждения аналогичны пункту 2).
![]()
![]()
![]()
4) Докажем единственность разложения по базису. Методом от противного. Пусть вектор а можно разложить по базису двумя разными способами.
![]()
![]() .
Из (2) вычтем (1):
.
Из (2) вычтем (1):
![]()
![]() а
это противоречит некомпланарности
базисных векторов. Полученное противоречие
доказывает единственность разложения
векторов. (ч.т.д.)
а
это противоречит некомпланарности
базисных векторов. Полученное противоречие
доказывает единственность разложения
векторов. (ч.т.д.)
Опираясь на свойства сложения и умножения векторов легко доказать следующие свойства:1) При умножении вектора на число его координаты умножаются на это число.
2) При сложении векторов соответствующие координаты этих векторов складываются.
