3) Алгоритм типа « разделяй и властвуй».
а)
Сортировка набора точек по
;
б) Последовательно разбивается до трех или четырех точек. Затем наборы триангулируются;
в) Последовательное соединение: могут создаваться LR-ребра, удаляться – LL и RR. Сначала ищется самое нижнее ребро, затем – две ближайшие верхние точки левой и правой триангуляции. Выбирается наилучший кандидат, то есть тот, окрестность которого не содержит другого кандидата. Этот кандидат становится нижним ребром.
Чтобы треугольники удовлетворяли условия Делоне, делается флип – переброска ребер.
Сложность:
Преимущества GRID:
проще процедура анализа;
точнее;
выглядит естественно.
Преимущества TIN:
быстро отображается;
лучше приспособлена к разрывам;
быстрее строится.
Дополнительные элементы:
Полигоны замещения, то есть
Полигоны отсечения – полигоны, внутри которых надо построить рельеф.
Линейные объекты – ребра, по которым должна проводиться триангуляция
------Билет 15. Триангуляция Делоне с ограничениями. Применение триангуляция Делоне для реализации пространственных операторов------
Дополнительные методы построения цифровой модели рельефа. Учет дополнений, ограничений элементов.
Триангуляция Делоне с ограничениями.
1. Полигон отсечения – граница, где строим триангуляцию;
2. Полигон замещения (озеро, река).
3. Структура линии реки.
Для
записи используется триангуляция Делоне
с ограничениями. Входные данные
и структурные ребра – соединяющие набор
точек.
- ребро из точек набора.
а)
Триангуляция состоит из треугольников
- ребро Делоне с ограничением.
б)
Все треугольники не 
структурной линии
-
условию Делоне.
Построение треугольника Делоне с ограничениями. Алгоритм.
1. Треугольник Делоне без ограничений.
2. Вставка ребер.
Все что примыкает не обязательно должно удовлетворять условию Делоне.
Если все точки полигона имеют одинаковую высоту, то изломов не будет.
Структура триангуляции.
VPoint record узлы
x, y ,z : double;
end;
TEdge = record
p1, p2: ptTPoint;
t1, t2: pTTriangle;
end;
TTriangle = record треугольники
p1, p2,p3: pTTPoint;
R1,
R2, R3: pTEdge
t1, t2, t3: pTTriangle;
end;
В треугольнике может храниться центр и радиус окружности.
Рассмотрим задачу:
Пусть есть триангуляция Делоне с ограничениями. Необходимо классифицировать треугольник на попадание в полигон.
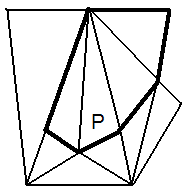
1)
Простая проверка:
- сложность.
2) Берем ребро и проверяем в каждой точке с одной и другой стороны ребра, алгоритм растровой заливки.
3) Выделение полигонов из триангуляции: у каждого треугольника индекс. Берется треугольник с определенным индексом, для него допускается алгоритм растровой заливки для каждого из индексов. Причем отличаются ребра, через которые прошла заливка и через которые не проходила. Поэтому отслеживаются граничные ребра – определяется полигон, используется для пространственного объединения.
1. Ищем точку пересечения полигонов – ребер.
2. На расширенном наборе точек определяем вершины.
3. Строим трианы Делоне для этих точек.
4. Классифицируем треугольник ON на попадание в треугольник.
5.
Выстроим новую индексацию:
.
6. Выделение полигона из трингуляции.
Достоинства: вычисление точное, хорошо обрабатываются случаи.
Полигоны Вороного (Тиссена) – полигоны ближайшего соседа.
