
- •------Билет 1. Понятие гис, ее суть, применение. Основные задачи гис------
- •Введение.
- •------Билет 2. Источники данных для гис. Технология ввода данных с различных источников------
- •Геодезические измерения.
- •------Билет 4. Семантические атрибуты пространственного объекта, шкалы. Пространственные атрибуты. Связь графической и семантической части объекта. ------
- •------Билет 5. Метрическая составляющая пространственного объекта. Модели хранения графических данных ------
- •------Билет 6. Пространственные отношения в гис. Понятие топологического редактирования.------ Пространственные отношения
- •Стандартные операции в ГиС.
- •Пространственная индексация.
- •Понятие топологического редактирования
- •------Билет 7. Методы отображения пространственных контуров------ Визуализация пространства контуров.
- •I. Тип «размножение»
- •Дистанционное зондирование.
- •------Билет 8. Генерализация------
- •------Билет 9. Тематические карты и их виды (без методов классификации)------
- •5) Метод диапазонов. ------Билет 10. Методы классификации при создании тематических карт методом диапазонов------
- •Методы разбиения на диапазоны:
- •------Билет 11. Операции над пространственными объектами (объединение, пересечение…). Построение буферных зон------ Пространственные операторы. Оверлей слоев.
- •------Билет 12. Язык пространственно-семантических запросов------ Пространственно-семантические запросы.
- •Введение к Билету 13. Цифровая модель рельефа (цмр)
- •------Билет 13. Grid-модель рельефа. Алгоритмы построения grid-моделей------
- •------Билет 14. Tin-модель. Алгоритмы триангуляции Делоне------
- •1) Триангуляционные (tin).
- •3) Алгоритм типа « разделяй и властвуй».
- •Структура триангуляции.
- •------Билет 16. Задачи на цмр (профили, подсчет площади и периметра, анализ видимости, преобразование tin-модели в растровую модель, построение линий уровня и пр.)------ Задачи на цмр.
- •------Билет 17. Физическая форма Земли. Системы координат. Пересчет между системами координат------ Эллиптическая система координат.
- •------Билет 18. Проекции и их виды. Проекция Гаусса-Крюгера------ Картографические проекции.
- •------Билет 19. Геометрическая коррекция растровых изображений (виды преобразований)------
- •------Билет 23. Моделирование инженерных и транспортных сетей в гис------ Моделирование инженерных и транспортных сетей.
------Билет 13. Grid-модель рельефа. Алгоритмы построения grid-моделей------
GRID- модели – модели регулярных ячеек.

Пусть
введена система координат
![]() и
и![]() и
и![]() .
Пользователь задает
.
Пользователь задает![]() и шаги дискретизации
и шаги дискретизации![]() .
.
![]()
 ,
,
![]()
 -
физические координаты точки.
-
физические координаты точки.
Вычисляем
![]() и
и![]() ,
,![]() - разрядная сетка.
- разрядная сетка.
![]() -
квантованные значения. Реальные:
-
квантованные значения. Реальные:
![]()

![]() -
параметр алгоритма – количество точек,
-
параметр алгоритма – количество точек,
![]() - вес. Чем ближе точка, тем больше вес.
- вес. Чем ближе точка, тем больше вес.
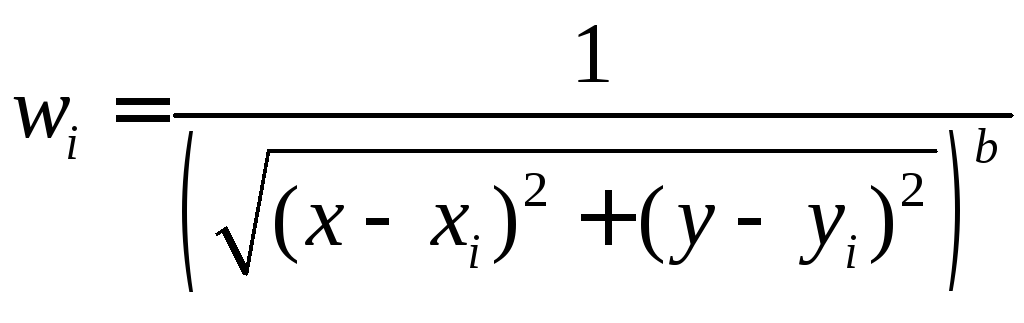
![]() -
степень расстояния (1 или 2).
-
степень расстояния (1 или 2).
Нормировочный
коэффициент: 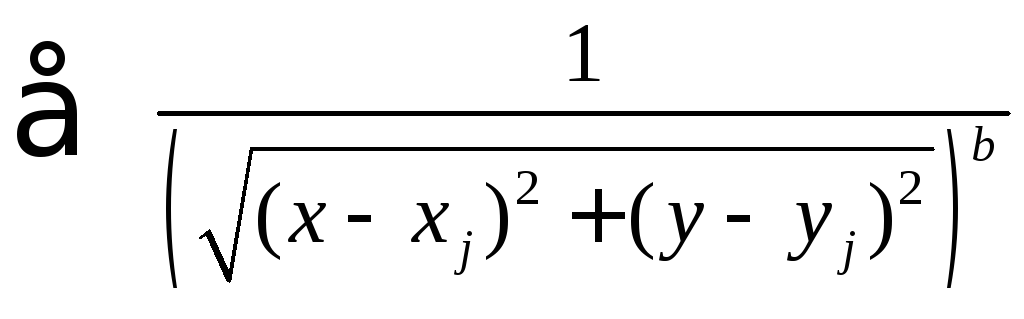
Чем
![]() ближе к 1, тем больше учитываются точки
с большим весом.
ближе к 1, тем больше учитываются точки
с большим весом.

Это
метод IDW – долгий, для каждой т. необходимо
найти соседей. Набор соседей может быть
эффективно найден - ближайшим. Каждая
из точек продуцирует «колышек»
определенной высоты. От нерегулярности
постановок точки многое зависит, для
этого берут
![]() или
или
![]() т.е. разделяют на сектора и в окрестности
точки строим.
т.е. разделяют на сектора и в окрестности
точки строим.
Преимущество – простота
Недостаток:
На значение высоты влияет набор точек. Чтобы этого избежать, матрицу разбивают на сектора и вводят коэффициенты
 или
или
 –локальные
экстремумы построенной функции.
–локальные
экстремумы построенной функции.
------Билет 14. Tin-модель. Алгоритмы триангуляции Делоне------
1) Триангуляционные (tin).
Триангуляция – построение функции в виде совокупности кусочно - линейной функции

Триангуляция – интерполяция внутри выпуклой области.
Триангуляция – планарный граф, все внутренние ребра которого – треугольники; способ представления пространства в виде примыкающих друг к другу треугольников без перекрытий. На наборе точек триангуляция строится несколькими способами.
![]()
Нужен алгоритм для построения оптимальной триангуляции.

Плоскость, проходящая через 3 точки.
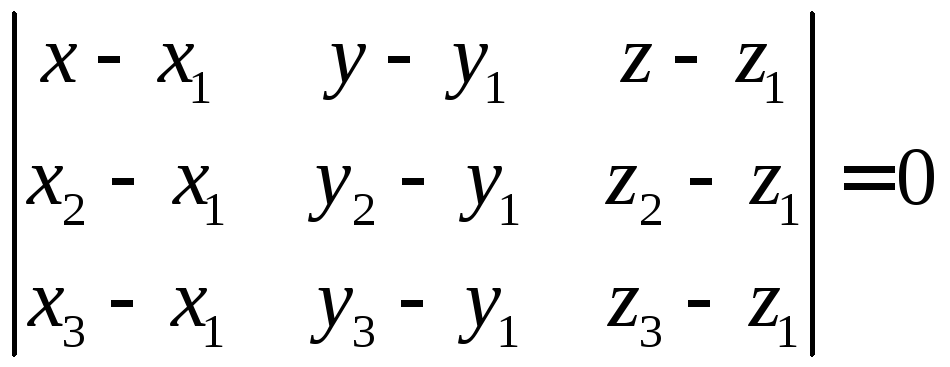
1)
Найдем треугольник, который
![]() ;
;
2)
![]() - строим уравнение плоскости.
- строим уравнение плоскости.
Чтобы проверить находятся ли точки внутри треугольника или нет, необходимо подставить значение в уравнение линий – ребер треугольника. Если все 3 уравнения > 0, то внутри.
Структура представления:
Каждая триангуляция содержит одинаковое количество треугольников.
![]() ,
где
,
где
![]() – количество внутренних точек,
– количество внутренних точек,![]() – количество точек.
– количество точек.
Жадный триангуляция.
Все точки соединяем ребрами, выбираем минимум, добавляем в триангуляцию. Далее берем следующий минимум, не пересекающийся с предыдущими и т.д. В результате получена жадная триангуляция.
Триангуляция Делоне.
Внутрь окружности, описанной вокруг любого треугольника, не попадают точки других треугольников. Строится единственным образом.

Флипом называется переброска ребер. Она позволяет перейти от обычной триангуляции к триангуляции Делоне. Чтобы проверить принадлежность точки к окружности: подставить, если < R, то внутри.
Условие Делоне.
Уравнение окружности, проходящей через три точки:
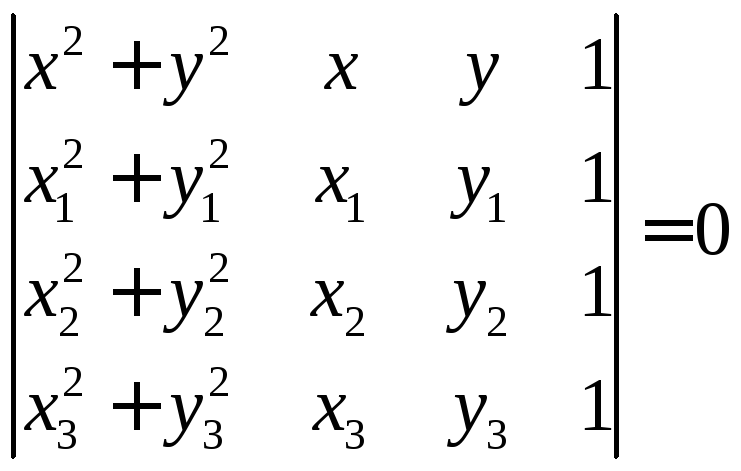
Если меньше нуля, то внешняя, иначе – внутренняя.
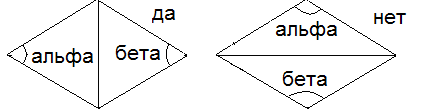
![]() –условие
Делоне.
–условие
Делоне.
Алгоритм построения триангуляции Делоне:
1) Подследственного добавления точек – простой итеративный алгоритм:
Есть
набор
![]() добавляем в треугольник, осуществляется
построение
добавляем в треугольник, осуществляется
построение![]() разбиение треугольника
разбиение треугольника![]() перестроение. На нулевом этапе добавляем
3-4 фиктивные точки, которые заведомо
покрывают наш конверт, все точки внутри.
После кидаем точку, смотрим в какой
треугольник попала, разбиваем на 3, для
каждого треугольника проверяем условие
Делоне и осуществляем флип переброску
ребер. Среднее количество перестроений
равно трем.
перестроение. На нулевом этапе добавляем
3-4 фиктивные точки, которые заведомо
покрывают наш конверт, все точки внутри.
После кидаем точку, смотрим в какой
треугольник попала, разбиваем на 3, для
каждого треугольника проверяем условие
Делоне и осуществляем флип переброску
ребер. Среднее количество перестроений
равно трем.
Теоретическая
сложность
![]()
2) Методы ускорения. Основан на статистически зависимых точках. Затравочный треугольник – треугольник в который попала предыдущая точка. Затем соединяем две точки – предыдущую и новую.
Перемещаемся из первой точки в другую.

