Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования "Самарский государственный аэрокосмический университет имени академика С.П. Королева (национальный исследовательский университет)"

Факультет экономики и управления Кафедра «Математические методы в экономике»

Дисциплина «Теория оптимального управления»

Лекции «Принцип максимума Понтрягина»

Выполнила: студентка гр.751 К.А. Литвиненко

Самара 2011

Принцип максимума Понтрягина формулирует необходимое условие оптимальности управления для нелинейных динамических систем и является необходимым и достаточным условием оптимальности в случае линейных динамических систем.

Формализм принципа максимума Понтрягина (вывод необходимых условий оптимальности)

Постановка задачи оптимального управления:

Требуется найти оптимальное управление динамической системы из класса допустимых управлений, переводящее динамическую систему из заданного начального в конечное состояние за интервал времени Т= t_k- t_o, при учете ограничений на фазовые переменные и управление, и обеспечивающее минимальное значение выбранного функционала.

Рассмотрим динамическую систему, где х – n-мерный вектор.

- производная

Вводится дополнительная фазовая переменная таким образом, чтобы функционал был равен конечному значению фазовой переменной.

𝓘(u) называется функционалом функции u(t) на отрезке времени t∈[t_o;t_k], если каждой функции u(t), принадлежащей некоторому классу функций, ставится в соответствие определенное число. Функционал является критерием качества задачи.

- аргумент минимизации функционала

Uopt(t)opt

τ -ε

τ

U(t)

ε

T

t

Игольчатая вариация управления

τ

T

t

}δ𝓘>0

t

T

τ

δx(τ)

𝓘min

x_opt(t)

δ𝓘=δx_n+1(T)>0

X(n+1)(t)

x(t)

для t>τ

Игольчатая вариация после ее приложения вызывает малые отклонения в поведении динамической системы от оптимального.

Введем дополнительный вектор (сопряженных переменных), размерность которого совпадает с размерностью вектора x.

Условия трансверсальности:

1. 

2. 

Продифференцируем первое условие

– изменение сопряженных переменных

Функция Гамильтона

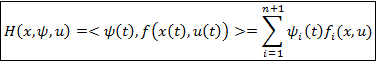
Оптимальное управление в каждый момент времени должно обеспечивать максимальное значение функции Гамильтона. (необходимое условие оптимальности Понтрягина)

Постановка обобщенной задачи:

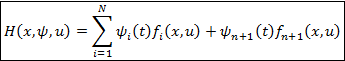
Каноническая система дифференциальных уравнений (2n+2)

Требования к конечным значениям сопряженных переменных:

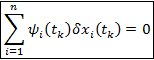
Свойства функции Гамильтона и поиск ее экстремума

1. Непрерывная функция времени

2. Функция Гамильтона при оптимальном управлении на оптимальной траектории является постоянной

3. Функция Гамильтона на оптимальной траектории при оптимальном управлении в случае нефиксированности конечного момента времени равна нулю

4. Если ограничения на управление отсутствуют, то оптимальное управление достигается в одной из стационарных точек функции Гамильтона

U

H

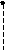
5. Если ограничения на управление существуют, то наряду со стационарными точками необходимо проверить значения, которые принимает функция Гамильтона на границах

H

U

Типы граничных условий и виды краевых задач

1)

	t0	tk
	xi(t0)=x0
	xn+1(t0)=xn+1,0
		𝜓i(tk)=0

Решение краевой задачи сводится к итерационной процедуре, основным элементом которой является задача Коши, и заключается в подборе недостающих (n+1) начальных условий для сопряженных переменных 𝜓 с целью, чтобы в конечный момент времени сопряженные переменные 𝜓 приняли заданные значения, вытекающие из условия трансверсальности.

2)

	t0	tk
	xi(t0)=x0	xi(t0)=x0
	xn+1(t0)=xn+1,0

3)

	t0	tk
	xi(t0)=x0	xi(tk)=x1k
	……..	…….
	xn(t0)=xn0	xm(tk)=xmk
	xn+1(t0)=xn+1,0
		𝜓m+1(tk)=0
		.........
		𝜓n(tk)=0