
- •Аккредитационные педагогические измерительные материалы
- •011000.62 Механика. Прикладная математика
- •Перечень вопросов
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика»
- •011000.62 Механика. Прикладная математика»
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
011000.62 Механика. Прикладная математика»
На основании какой теоремы устанавливается дифференциальная форма равновесия?
а
Остроградского-Гаусса.
б
Стокса.
в
Грина.
Укажите функцию Эри.
Что такое кривая текучести?а
 .
.б
 .
.в
 .
.
Что такое поверхность нагружения?а
Пересечение поверхности
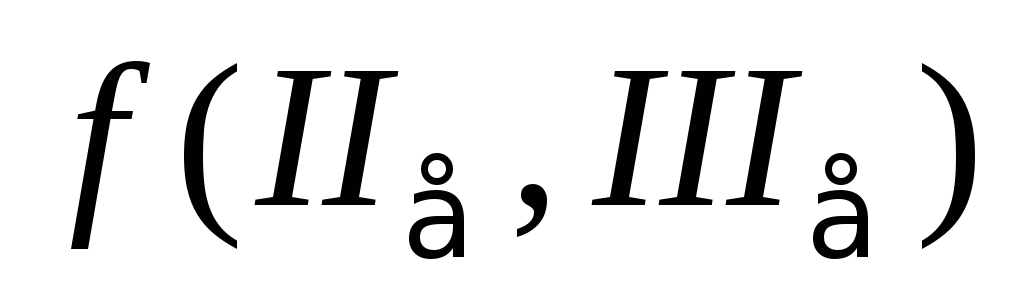 с девиаторной плоскостью.
с девиаторной плоскостью.б
Пересечение поверхности
 с плоскостью
с плоскостью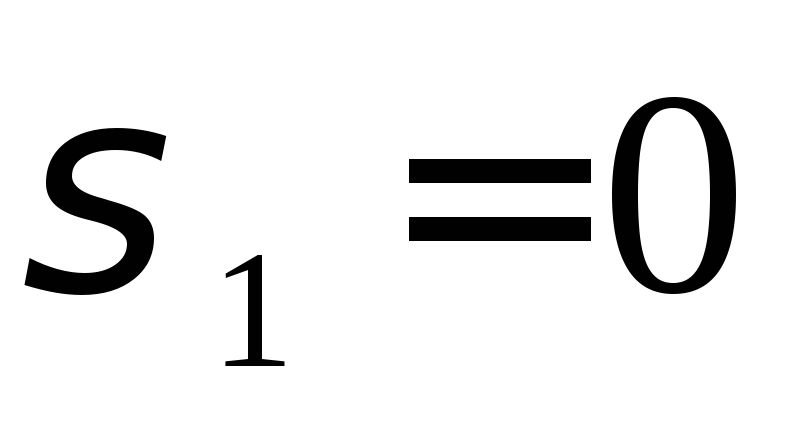 .
.в
Пересечение поверхности
 с плоскостью
с плоскостью .
.
Укажите соотношение для модели упругого поведения материала.а
Поверхность текучести для упругого материала.
б
Поверхность деформирования для упрочняющегося материала.
в
Поверхность текучести для упрочняющегося материала.
Что практически описывает модель Максвелла?а
 .
.б
 .
.в
 .
.
Укажите выражение для плотности энергии деформации.а
Модель Максвелла описывает релаксацию.
б
Модель Максвелла описывает эффект ползучести.
в
Модель Максвелла описывает эффект ползучести и релаксацию.
Уравнение неразрывности в форме Лагранжа имеет вид:а
 .
.б
 .
.в
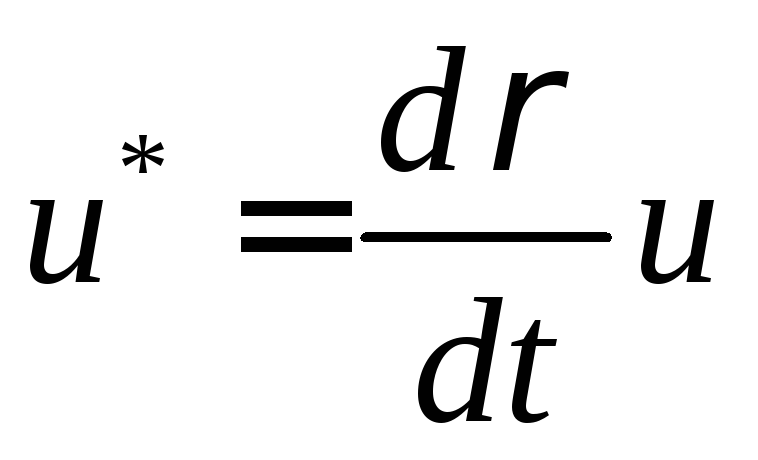 .
.а
 .
.б
 .
.в
 .
.Что такое мгновенная скорость частицы?
а
Скорость изменения со временем любого свойства движущейся среды.
б
Скорость изменения со временем любого свойства в индивидуальных частицах движущейся среды.
в
Материальная производная по времени от положения частицы.
Укажите формулу, описывающую связь лагранжевых и эйлеровых координат в теории малых деформаций.
|
а |
|
|
б |
|
|
в |
|
-
Разработчик
/А. И. Хромов/
23 декабря 2012 г.
БИЛЕТ № 4
контроля остаточных знаний студентов
по дисциплине «МЕХАНИКА ДЕФОРМИРУЕМОГО ТВЕРДОГО ТЕЛА»
Специальность
011000.62 Механика. Прикладная математика
Когда напряженные состояния называют простыми?
а
Когда одно или два главных значения равны 0.
б
Когда все главные значения равны 0.
в
Когда все главные значения не равны 0.
В чем состоит единственность решений задач теории упругости?
Укажите критерий Мизеса.а
В постановке задач линейной теории упругости, поля напряжений и деформаций единственны.
б
В постановке задач линейной теории упругости, поля напряжений единственны.
в
В постановке задач линейной теории упругости, поля перемещений и деформаций единственны.
В чем состоит эффект релаксации для модели Кельвина?а
 .
.б
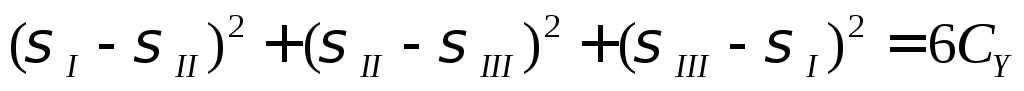 .
.в
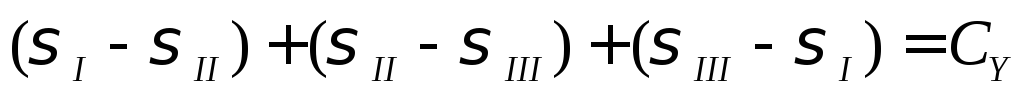 .
.
Укажите уравнение сохранения энергии для линейной теории упругости.а
В увеличении деформации со временем при постоянном напряжении,
 ,
, .
.б
В увеличении напряжения со временем при постоянной деформации,
 ,
, .
.в
В уменьшении напряжения со временем при постоянной деформации,
 ,
, .
.
Каковы условия несжимаемости среды?а
 .
.б
 .
.в
 .
.а
 ,
,
 .
.б
 ,
,
 .
.в
 ,
,
 .
.Что такое нагружение, разгрузка, с учетом формулы
 ?
?
Формулы определения материальной производной при лагранжевой и эйлеровой формах задания сплошной среды определяются:а
разгрузка:
 и
и ,
нейтральное нагружение:
,
нейтральное нагружение: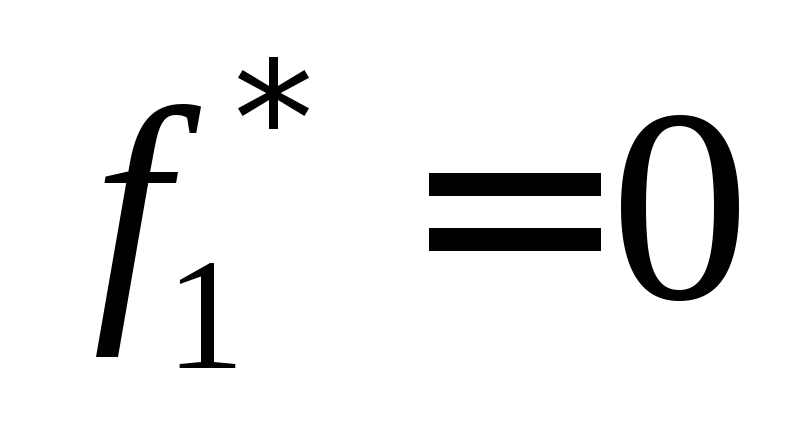 и
и ,
,активное нагружение:
 и
и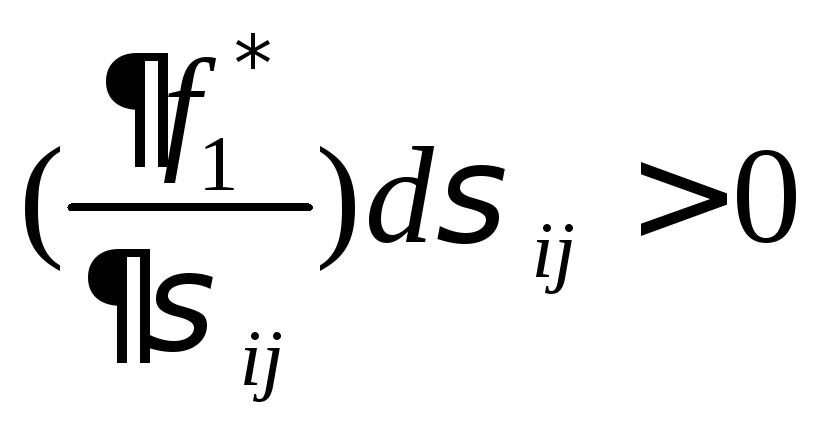 .
.б
разгрузка:
 и
и ,
нейтральное нагружение:
,
нейтральное нагружение: и
и ,
,активное нагружение:
 и
и .
.в
разгрузка:
 и
и ,
нейтральное нагружение:
,
нейтральное нагружение: и
и ,
,активное нагружение:
 и
и .
.а
 - если независимыми переменными
являются
- если независимыми переменными
являются ,
, - если независимыми переменными
являются
- если независимыми переменными
являются .
.б
 -
если независимыми переменными
являются
-
если независимыми переменными
являются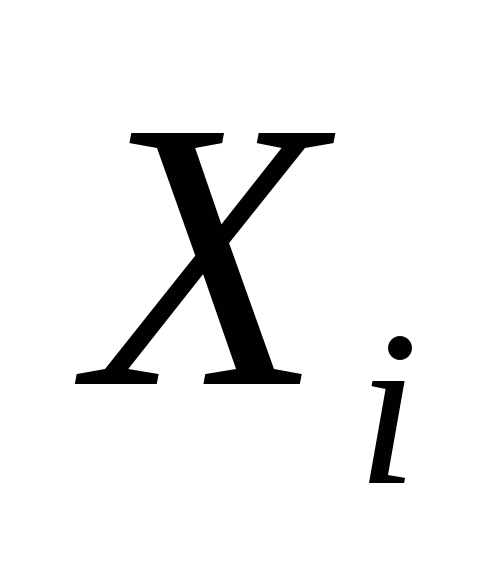 ,
, - если независимыми переменными
являются
- если независимыми переменными
являются .
.в
 -
если независимыми переменными
являются
-
если независимыми переменными
являются ,
, - если независимыми переменными
являются
- если независимыми переменными
являются .
.В чем состоит геометрический смысл диагональных элементов тензора линейных деформаций?
|
а |
Диагональные члены тензора линейных деформаций представляют собой коэффициенты изменения угла. |
|
б |
Диагональные члены тензора линейных деформаций представляют собой коэффициенты относительного удлинения элементов. |
|
в |
Диагональные члены тензора линейных деформаций представляют собой коэффициенты относительного удлинения элементов вдоль координатных осей. |
Как определяется девиатор напряжений?
|
а |
|
|
б |
|
|
в |
|
-
Разработчик
/А. И. Хромов/
23 декабря 2012 г.
БИЛЕТ № 5
контроля остаточных знаний студентов
по дисциплине «МЕХАНИКА ДЕФОРМИРУЕМОГО ТВЕРДОГО ТЕЛА»
Специальность
