
- •Аккредитационные педагогические измерительные материалы
- •011000.62 Механика. Прикладная математика
- •Перечень вопросов
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика»
- •011000.62 Механика. Прикладная математика»
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
- •011000.62 Механика. Прикладная математика
011000.62 Механика. Прикладная математика
Что называется вектором напряжения?
а
 .
.б
 .
.в
 .
.Какими формулами определяются градиенты деформации?
а
 и
и .
.б
 и
и .
.в
 и
и .
.Индивидуальная производная – это…
Какой закон выражает уравнение неразрывности?а
Материальная производная по времени от положения частицы.
б
Скорость изменения со временем любого свойства движущейся среды.
в
Скорость изменения со временем любого свойства в индивидуальных частицах движущейся среды.
Укажите уравнение сохранения энергии для линейной теории упругости.а
Закон сохранения энергии.
б
Закон сохранения массы.
в
Закон сохранения импульса.
|
а |
|
|
б |
|
|
в |
|
В чем состоит эффект Баушингера?
Укажите соотношение для модели Кельвина.а
Свойство материала изменять предел текучести на сжатие при его растяжении.
б
Свойство материала уменьшать предел текучести на сжатие при его растяжении.
в
Свойство материала увеличивать предел текучести на сжатие при его растяжении.
Укажите критерий Мизеса.а
 .
.б
 .
.в
 .
.
В чем состоит эффект ползучести для модели Кельвина?а
 .
.б
 .
.в
 .
.
Как определяется тензор скоростей деформации?а
В увеличении деформации со временем при постоянном напряжении,
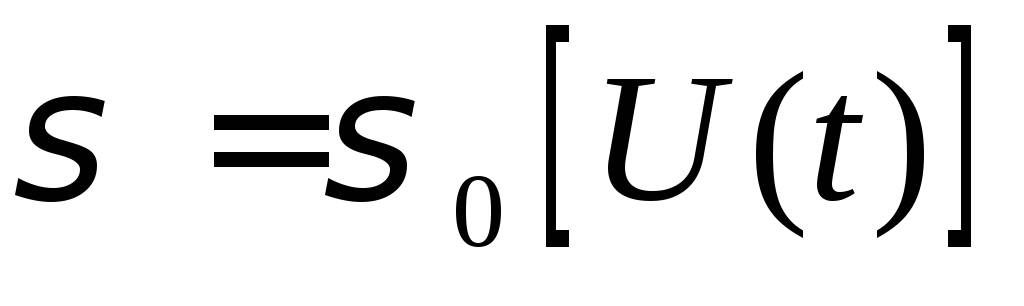 ,
, .
.б
В уменьшении напряжения со временем при постоянной деформации,
 ,
, .
.в
В увеличении напряжения со временем при постоянной деформации,
 ,
, .
.
|
а |
|
|
б |
|
|
в |
|
-
Разработчик
/А. И. Хромов/
23 декабря 2012 г.
БИЛЕТ № 21
контроля остаточных знаний студентов
по дисциплине «МЕХАНИКА ДЕФОРМИРУЕМОГО ТВЕРДОГО ТЕЛА»
Специальность
011000.62 Механика. Прикладная математика
Какой формулой выражается принцип напряжения Коши?
а
 .
.б
 .
.в
 .
.Укажите формулы для тензоров деформаций, и тензоров конечных деформаций.
а
 -
тензор деформаций Коши,
-
тензор деформаций Коши, -
тензор деформаций Грина;
-
тензор деформаций Грина; - тензор конечных деформаций Грина,
- тензор конечных деформаций Грина, - тензор конечных деформаций Альманси.
- тензор конечных деформаций Альманси.б
 -
тензор деформаций Коши,
-
тензор деформаций Коши, -
тензор деформаций Грина;
-
тензор деформаций Грина; - тензор конечных деформаций Грина,
- тензор конечных деформаций Грина, - тензор конечных деформаций Альманси.
- тензор конечных деформаций Альманси.в
 -
тензор деформаций Коши,
-
тензор деформаций Коши, -
тензор деформаций Грина;
-
тензор деформаций Грина; - тензор конечных деформаций Грина,
- тензор конечных деформаций Грина, - тензор конечных деформаций Альманси.
- тензор конечных деформаций Альманси.Как определяются якобианы прямого и обратного отображения при движении сплошной среды?
Какую запись имеет закон сохранения массы в дифференциальной форме?а
 - прямое,
- прямое, - обратное.
- обратное.б
 - прямое,
- прямое, - обратное.
- обратное.в
 - прямое,
- прямое, - обратное.
- обратное.
Укажите основные предположения линейной теории упругости.а
 .
.б
 .
.в
 .
.
Укажите общий вид условия пластичности для изотропного и анизотропного материала.а
 и
и .
.б
 и
и .
.в
 и
и .
.
Укажите соотношение для модели вязкого поведения материала.а
Для изотропного
 ,
для
анизотропного
,
для
анизотропного .
.б
Для изотропного
 ,
для
анизотропного
,
для
анизотропного .
.в
Для изотропного
 ,
для
анизотропного
,
для
анизотропного .
.
|
а |
|
|
б |
|
|
в |
|
Укажите формулу преобразования компонент тензора деформации при ортогональном преобразовании декартовой системы координат.
В чем состоит ассоциированный закон пластического течения?а
Часть поверхности тела, где заданы поверхностные силы
б
Часть поверхности тела, где заданы объёмные силы
в
Часть поверхности тела, где заданы перемещения
Укажите формулы представления тензоров конечных деформаций через вектор перемещений.а
 .
.б
 .
.в
 .
.
|
а |
|
|
б |
|
|
в |
|
-
Разработчик
/А. И. Хромов/
23 декабря 2012 г.

 .
. .
. .
. и
и .
. и
и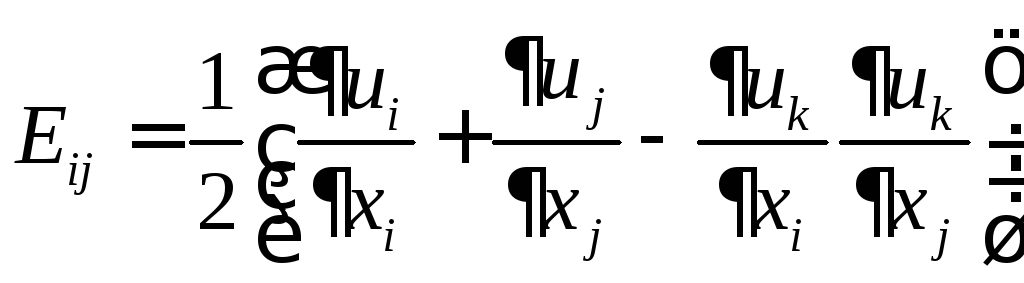 .
. и
и .
.