
- •010501 Прикладная математика и информатика
- •2.1. Случайные величины. Функция распределения случайной величины и ее свойства
- •2.2. Дискретные случайные величины. Закон распределения дискретной случайной величины.
- •2.3. Важнейшие дискретные случайные величины и их законы распределения
- •2.4. Непрерывные случайные величины. Плотность вероятностей
- •2.5. Важнейшие непрерывные случайные величины
2.4. Непрерывные случайные величины. Плотность вероятностей
Определение.
Случайная величина
![]() ,
заданная на вероятностном пространстве
,
заданная на вероятностном пространстве
![]() ,называется
непрерывной
или имеющей непрерывный
закон распределения,
если существует такая функция
,называется
непрерывной
или имеющей непрерывный
закон распределения,
если существует такая функция
![]() ,
что для любого
,
что для любого![]() функция распределения
функция распределения![]() случайной величины
случайной величины![]() допускает представление:
допускает представление:
 .
(2.3)
.
(2.3)
При этом функция
![]() называетсяплотностью
вероятностей
(плотностью распределения вероятностей,
плотностью распределения) случайной
величины
называетсяплотностью
вероятностей
(плотностью распределения вероятностей,
плотностью распределения) случайной
величины
![]() .
.
Замечание.
Для существования интеграла (2.3)
предполагается, что плотность вероятностей
![]() является функцией непрерывна всюду, за
исключением, может быть, конечного числа
точек.
является функцией непрерывна всюду, за
исключением, может быть, конечного числа
точек.
Из определения следует:
1. Если случайная
величина
![]() является непрерывной, то ее функция
распределения
является непрерывной, то ее функция
распределения![]() непрерывна
на всей числовой прямой.
непрерывна
на всей числовой прямой.
(Это следует из свойств интеграла с переменным верхним пределом).
Следствие.
Если случайная величина
![]() является непрерывной, то
является непрерывной, то
![]() для любого
для любого
![]() .
(2.4)
.
(2.4)
2. Если случайная
величина
![]() является непрерывной, то ее функция
распределения
является непрерывной, то ее функция
распределения![]() являетсядифференцируемой
во всех точках, где плотность вероятностей
являетсядифференцируемой
во всех точках, где плотность вероятностей
![]() непрерывна, и при этом справедливо
равенство:
непрерывна, и при этом справедливо
равенство:
![]() .
(2.5)
.
(2.5)
(Этот факт также следует из свойств интеграла с переменным верхним пределом).
В точках, где
плотность вероятностей
![]() непрерывной не является, производная
функции распределения
непрерывной не является, производная
функции распределения![]() не существует. Это означает, что в этих
точках функция распределения
не существует. Это означает, что в этих
точках функция распределения![]() ,
являясь функцией непрерывной, имеетизлом,
так что
,
являясь функцией непрерывной, имеетизлом,
так что
![]() .
Но таких точек в соответствии с замечанием
не более конечного числа и в них плотность
вероятностей может быть задана произвольно
(на величине интеграла (2.3) и на вероятностях
событий, связанных со случайной величиной,
в соответствии с (2.4) это никак не
отражается).
.
Но таких точек в соответствии с замечанием
не более конечного числа и в них плотность
вероятностей может быть задана произвольно
(на величине интеграла (2.3) и на вероятностях
событий, связанных со случайной величиной,
в соответствии с (2.4) это никак не
отражается).
Замечание.
Говорят также, что равенство (2.5)
выполняется «почти всюду» или «для
почти всех
![]() »,
понимая под этим справедливость равенства
«везде» или «для всех
»,
понимая под этим справедливость равенства
«везде» или «для всех![]() »,
кроме (возможно)
»,
кроме (возможно)![]() из некоторого множества нулевой меры
(длины). Используя данную терминологию,
можно сказать, что функция распределения
непрерывной случайной величины является
дифференцируемой почти всюду.
из некоторого множества нулевой меры
(длины). Используя данную терминологию,
можно сказать, что функция распределения
непрерывной случайной величины является
дифференцируемой почти всюду.
Геометрическая иллюстрация.

Из равенства (2.5) и определения производной следует, что
![]() .
.
Интерпретируя
вероятность
![]() как массу, приходящуюся на интервал
как массу, приходящуюся на интервал![]() ,
отношение
,
отношение![]() представляет собой среднюю плотность
массы на этом интервале, а в пределе при
представляет собой среднюю плотность
массы на этом интервале, а в пределе при![]() получаем плотность массы в точкех.
Это обстоятельство и оправдывает
использование термина «плотность» для
функции
получаем плотность массы в точкех.
Это обстоятельство и оправдывает
использование термина «плотность» для
функции
![]() .
.
Формулы (2.3) и (2.5)
показывают, что между функцией
распределения
![]() непрерывной случайной величины и
плотностью вероятностей
непрерывной случайной величины и
плотностью вероятностей![]() существует взаимно однозначное
соответствие. Поэтому по аналогии с
дискретным случаем плотность вероятностей
можно называть законом распределения
непрерывной случайной величины или
непрерывным законом распределения.
существует взаимно однозначное
соответствие. Поэтому по аналогии с
дискретным случаем плотность вероятностей
можно называть законом распределения
непрерывной случайной величины или
непрерывным законом распределения.
Свойства плотности вероятностей
f1).
Плотность вероятностей
![]() является функцией неотрицательной:
является функцией неотрицательной:
![]() для любого
для любого
![]() .
.
▲ Поскольку функция
распределения
![]() является функцией неубывающей, то ее
производная
является функцией неубывающей, то ее
производная![]() .
Поэтому свойство следует из равенства
(2.5) ■.
.
Поэтому свойство следует из равенства
(2.5) ■.
f2).
Площадь под графиком плотности
вероятностей
![]() равна единице:
равна единице:
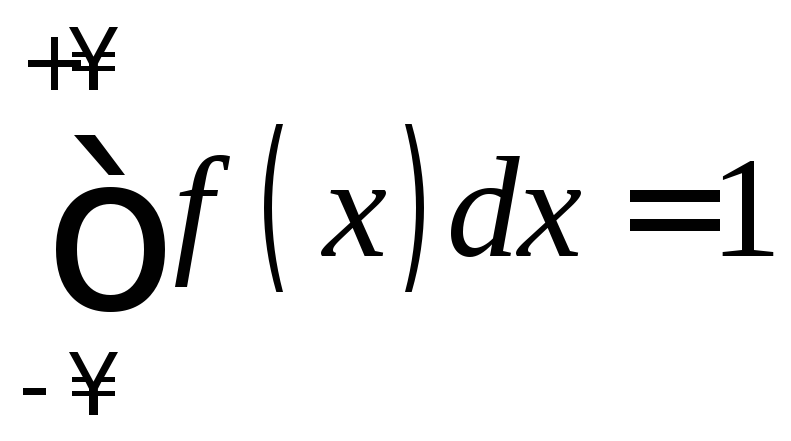 - условие
нормировки.
- условие
нормировки.
▲ Из представления
(2.3) следует, что
 ,
а в соответствии со свойствомF2)
функции распределения
,
а в соответствии со свойствомF2)
функции распределения
![]() ■.
■.
f3).
Вероятность попадания непрерывной
случайной величины
![]() в интервал
в интервал![]() определяется как интеграл от плотности
вероятностей по этому интервалу: для
любых
определяется как интеграл от плотности
вероятностей по этому интервалу: для
любых![]()
 .
(2.6)
.
(2.6)
▲ Поскольку в
соответствии со свойством F6)
функции распределения
![]() ,
то данное свойство непосредственно
вытекает из представления (2.3):
,
то данное свойство непосредственно
вытекает из представления (2.3):
 ■.
■.
Следствие.
Для непрерывной случайной величины
![]()
![]()
и все вероятности определяются с помощью интеграла (2.6).
Графическая иллюстрация функции распределения и плотности вероятностей непрерывной случайной величины.

