Самарский государственный аэрокосмический

университет имени академика С.П. Королева

Кафедра «Техническая кибернетика»

ТЕОРИЯ ВЕРОЯТНОСТЕЙ

И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Курс лекций

для студентов, обучающихся по специальности

010501 Прикладная математика и информатика

Случайные величины

Лектор: к.ф.-м.н., доцент

Коломиец Э.И.

САМАРА 2011

2.1. Случайные величины. Функция распределения случайной величины и ее свойства

Интуитивное представление о случайной величине

Случайная величина – это числовая функция, значения которой заранее (до наблюдения) нельзя точно определить, то есть функция, зависящая от случайного исхода и принимающая свои значения с некоторыми вероятностями.

Примеры случайных величин:

а) число пассажиров в автобусе (конечное число значений);

б) число вызовов на телефонной станции за время Т (счетное число значений);

в) время безотказной работы прибора за время Т (несчетное число значений).

Обозначают случайные величины прописными буквами латинского алфавита X, Y, Z,…, а их значения соответствующими строчными буквами x, y, z,….

Определение случайной величины

Пусть задано некоторое вероятностное пространство .

Определение. Функция называетсяслучайной величиной, если для любого множество

является событием, то есть .

Смысл приведенного определения случайной величины состоит в требовании того, чтобы у подмножества была определена его вероятность при любом.

Определение. Говорят, что функция является-измеримой, если множестводля любого.

Таким образом, случайная величина есть -измеримая функция, ставящая в соответствие каждому элементарному исходучисло.

Из определения случайной величины и свойств -алгебры вытекает, что событиями являются также следующие подмножества, связанные со случайной величиной:

;

;

;

,

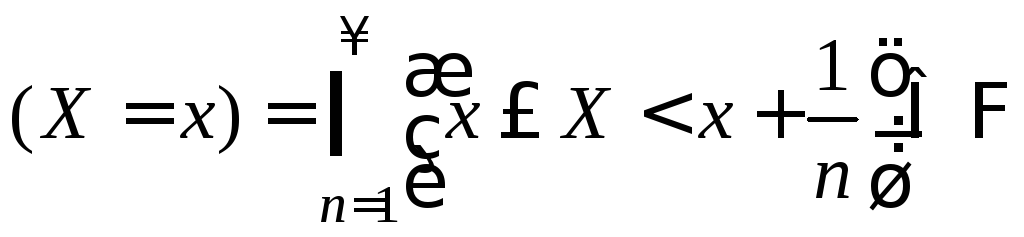и любые другие, получающиеся из них с помощью выполнения конечного или счетного числа операций. Другими словами, приведенное определение случайной величины эквивалентно тому, что попадание случайной величины в любое борелевское множество на числовой прямой является событием:для любого.

Заметим, что, если в -алгебресодержатся все подмножества(как, например, в случае конечного или счетного), то случайной величиной являетсялюбая числовая функция . В общем случае это не так.

Определение функции распределения случайной величины

Для того, чтобы определять вероятности событий, связанных со случайными величинами, и делать это одним и тем же способом для любых случайных величин, в теории вероятностей вводится понятие функции распределения.

Определение. Функцией распределения случайной величины называется функция, определенная при каждомравенством:

.

Из определения случайной величины следует, что ее функция распределения определена для любого.

Геометрически функция распределения означает вероятность попадания случайной точкилевее заданной точки:

Свойства функции распределения

Функция распределения является исчерпывающей вероятностной характеристикой случайной величины, поскольку позволяет определять вероятности любых событий с ней связанных. Это вытекает из следующих ее свойств функции распределения.

F0). для любого.

(свойство следует из определения, так как - вероятность).

F1). Функция распределения является функциейнеубывающей: .

▲ . Поэтому в силу свойства 3 вероятности ■.

F2). .

▲ Нестрогое доказательство данного свойства и его смысл состоят в следующем:

в силу свойства 2 вероятности;

в силу аксиомы нормированности Р2).

Строгое доказательство свойства F2) основано на использовании аксиомы непрерывности Р4).

Рассмотрим события ,. Нетрудно заметить, что последовательность событийудовлетворяет свойствам: 1); 2)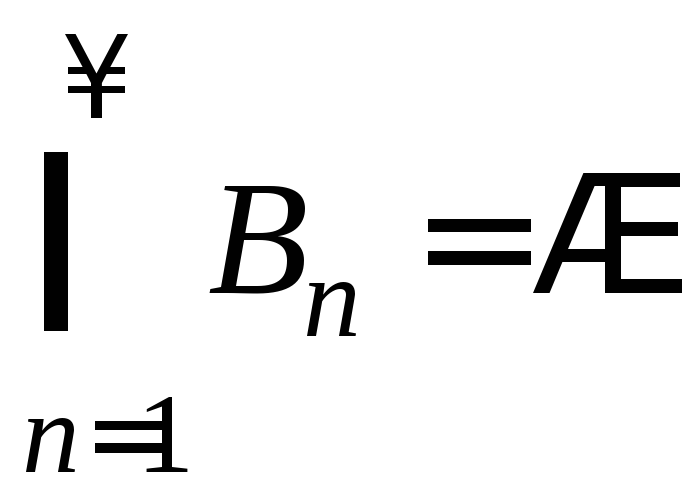. Поэтому в силу аксиомы непрерывности

.

Свойствам аксиомы непрерывности удовлетворяют также события ,и поэтому. Поскольку, то■.

F3). Функция распределения является функциейнепрерывной слева, то есть для любого

,

где - предел слева функции распределения в точкех.

▲ Рассмотрим события ,. В силу аксиомы непрерывности. Поскольку

,

то ■.

Замечание. Отметим, что если функцию распределения определить как , то она будет функцией непрерывной справа.

Замечание. Свойства F1), F2) и F3) полностью описывают класс функций распределения в смысле следующего утверждения (без доказательства).

Если функция удовлетворяет свойствамF1), F2) и F3), то есть функция распределения некоторой случайной величины, то есть найдется вероятностное пространствои такая случайная величина на этом пространстве, что.

F4). Для любого

,

где - предел справа функции распределения в точкех, - величина скачка функции распределения в точке.

Следствие. Если функция распределения непрерывна в точке , то. Если функция распределения непрерывна для любого, тодля любого.

▲ Поскольку справедливо представление

и события в сумме являются попарно несовместными, то в силу аддитивности вероятности

.

Доказательство свойства следует из того, что последовательность событий ,удовлетворяет аксиоме непрерывности и поэтому■.

F5). Для любого

.

▲ Действительно,

■.

Замечание. Геометрически свойства F3), F4) и F5) означают следующее. В точках , где функция распределения имеет разрыв 1 рода, то есть когда, за значение функции распределения принимается левое (нижнее, меньшее). При этом вероятность событияявляется ненулевой и ее значение равно величине скачка. В точках непрерывности функции распределения свойстваF3) F4) и F5) содержательными не являются.

F6). Вероятность попадания случайной величины в интервалопределяется как приращение функции распределения на этом интервале:

для любых

.

▲ Поскольку и события в сумме являются несовместными, то в силу аддитивности вероятности

или, что эквивалентно,

■.

F7). .

F8). .

F9). .

(Доказать свойства F7), F8) и F9) самостоятельно).

В общем случае график функции распределения может иметь вид:

В приложениях, как правило, встречаются случайные величины, функции распределения которых являются либо везде кусочно-постоянными (дискретные случайные величины), либо везде непрерывными и даже гладкими (непрерывные случайные величины). В каждом из этих случаев существуют более удобные, чем функция распределения, вероятностные характеристики случайных величин.