
Король А. В. / Практики Король А. В. / (4) Электростатическое поле в вакууме Часть 1
.pdf
1Задачи по теме "Электростатическое поле в вакууме: Часть I."
1.1Задача 1.
Во сколько раз сила кулоновского притяжения электрона к ядру атома водорода (протон) больше силы их гравитационного притяжения? Заряд электрона qe = −1.6 × 10−19 Кл, а его масса me = 9.1 × 10−31 кг. Заряд протона qp = 1.6 × 10−19 Кл, а его масса примерно в две тысячи раз больше электронной, mp ≈ 2000mp.
Решение.
Протон и электрон можно считать материальными точками и, соответственно, точечными зарядами. Тогда, сила гравитационного притяжения, Fг, находится напрямую из закона всемирного тяготения, а сила электростатического притяжения, Fэ, - из закона Кулона. Обозначив через r
расстояние между частицами, записываем: |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
memp |
|
|
|
2000m2 |
|
|
|
|
|
|
||||||||||
8 Fг = G |
|
|
|
|
|
|
≈ G2 |
|
e |
, |
|
|
|
|
|
|
||||||||
|
|
r2 |
|
|
r2 |
|
|
|
|
|
(1) |
|||||||||||||
> |
|
|
|
qe qp |
|
|
qp |
|
|
|
|
|
|
|
|
|
||||||||
< Fэ = k |
| |
| |
|
= k |
|
, |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
r2 |
|
r2 |
|
|
|
|
|
|
|
|
|||||||||||
> |
|
|
|
|
|
|
|
11 |
|
|
2 |
|
|
2 |
, и k = 1/4πϵ0 |
= 9 |
× 10 |
9 |
2 |
/Кл |
2 |
|||
где G:= 6.67 × 10− |
|
|
Н м |
/кг |
|
Н м |
в системе единиц СИ. |
|||||||||||||||||
Деля почленно второе уравнение на первое, находим отношение сил: |
||||||||||||||||||||||||
|
Fэ |
1 |
|
|
|
k |
|
qp |
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
≈ |
|
|
|
|
|
≈ 2 × 1039 1 . |
|
|
|
|
(2) |
|||||||||||
|
Fг |
2000 |
G |
me |
|
|
|
|
||||||||||||||||
Этот результат поясняет, почему в явлениях микромира (молекулярная, атомная физика, физика элементарных частиц) гравитационное взаимодействие не играет никакой роли, будучи исчезающе малым по сравнению с электростатическим (более общо, с электромагнитным) взаимодействием.
1.2 Задача 2.
В вершинах равностороннего треугольника нахо- |
|
|
дятся одинаковые положительные заряды q = 2 |
|
|
нКл. Какой отрицательный заряд необходимо поме- |
|
|
стить в центр треугольника, чтобы сила притя- |
|
|
жения с его стороны уравновесила силы отталки- |
F |
|
вания положительных зарядов? |
||
12 |
||
|
Q1 |
A |
Q F |
|
F |
β |
α |
2 |
|
|
Q 3 |
|
Q2 |
F
1
Решение.
Для определенности пронумеруем заряды, находящиеся в вершинах (см. рис.). Для рассмотрения, выберем заряд q3. На него действуют силы отталкивания F11 и F2 со стороны q1 и q3 и сила притяжения F со стороны Q. Компенсация всех сид требует выполнения векторного равенства, и, как следствие, скалярного равенства:
F1 + F2 + F = 0 = |F1 + F2| = F . |
(3) |
1Жирные буквы обозначают векторы!
1
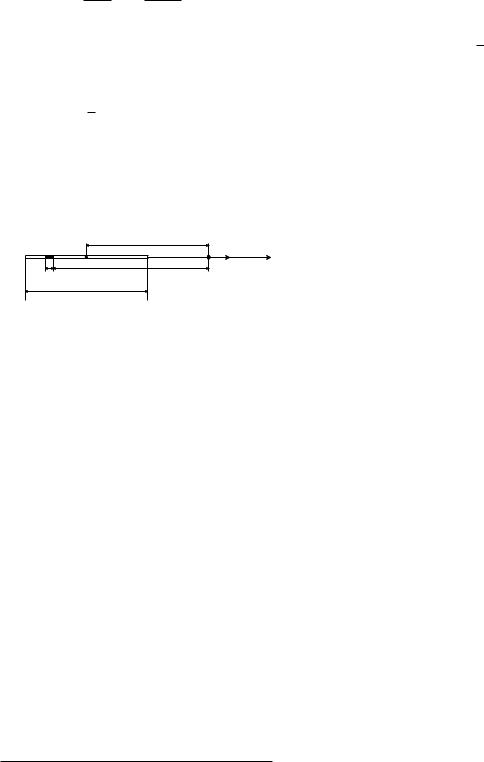
Сумма сил отталкивания F12 = F1 + F2, одинаковых по модулю, направлена по биссектрисе угла при вершине (β = α/2 = π/6) противоположно силе F. Модуль вектора F12 выражается через модуль F1 (равный F2): F12 = 2F1 cos β.
|
q2√ |
|
|
F12 = 2F1 cos β = k |
3 |
. |
|
a2 |
|||
Величина силы притяжения равна
q|Q| 3q|Q| F = k l2 = k a2 .
Здесь учтено, что расстояние l от центра равностороннего треугольника до его вершины выра- |
|
жается через сторону a следующим образом: l = a/(2 cos β) = a/√3. |
|
Приравнивая F12 к F , находим ответ: |
|
q |
(4) |
Q = √3. |
|
1.3Задача 3.
Заряд Q равномерно распределен по тонкому2 стержню длины L. На расстоянии r от центра O стержня, измеренного вдоль оси стержня, находится точечный заряд q. С какой силой взаимодействуют заряды?
|
|
r |
|
|
|
dE |
E |
|
O |
q |
|
|
|
|
|
dx |
|
x |
|
|
L |
|
|
Решение.
Заряд Q не является точечным, поэтому напрямую использовать закон Кулона нельзя. Единственное, что можно сказать сразу о взаимодействии зарядов, это то что они притягиваюся, если Qq < 0 и отталкиваются при Qq > 0.
Для определенности, будем полагать оба заряда положительными.
Для решения задачи, найдем напряженность E электрического поля, создаваемого зарядом Q в точке нахождения заряда q. Зная напряженность, силу действующую на q вычислим как
F = qE . |
(5) |
Для нахождения E "разобьём" стержень на точечные заряды. Для этого, разделим его на бесконечно-малые элементы длиной dx, см. рис. Заряд Q распределен равномерно, поэтому на единицу длины стержня приходится заряд λ = Q/L (λ называется линейной плотностью заряда, [λ] = Кл/м). Следовательно, на элементе dx находится бесконено-малый заряд dQ = λdx. Ввиду малости dx заряд dQ является точечным. Величина напряжённости dE электрического поля,
создаваемого dQ в точке нахождения заряда q, равна |
|
|||||
dE = k |
dQ |
= k |
λdx |
, |
(6) |
|
x2 |
x2 |
|||||
|
|
|
|
|||
где x - расстояние между dQ и q. Направление вектора dE указано на рисунке (учтено, что dQ > 0).
По принципу суперпозиции, напряженность E есть сумма напряженностей dE полей, созданных каждым зарядом dQ в отдельности. Поскольку все dE сонаправлены, то и вектор E
2Термин "тонкий" означает, что толщиной стержня можно пренебречь.
2
направлен так же. Следовательно, принцип суперпозиции можно применить для величины напряженности E. Суммируем dE, созданные всеми элементами стержня (от самого близкого к заряду q, расположенному на расстоянии x = r − L/2, до самого далекого, - на расстоянии x = r + L/2):
|
|
|
|
|
|
|
|
− |
|
x |
r L/2 |
|
r |
|
=Q |
|
|
4 |
|
|
|
|
|
|
|
4 |
|
|
||
r |
|
L/2 |
Z |
r L/2 |
|
|
|
|
|
|
z}|{ |
|
|
|
|
|
|
|
|
|
|
|||||||||
E = |
r+L/2 dE = |
r+L/2 k |
λdx |
= |
|
kλ |
1 |
|
r+L/2 |
= k |
|
|
λL |
|
|
|
= k |
|
|
Q |
|
|
|
. |
(7) |
|||||
|
|
|
− |
|
|
− |
|
|
|
|
|
|
− |
|
|
|
|
|||||||||||||
Z |
− |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
2 |
|
|
2 |
/ |
|
|
r |
2 |
|
|
2 |
/ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
L |
|
|
|
||||||
Силу взаимодействия зарядов Q и q получаем, используя (??) (5):
(8) |
|
F = qE = k r2 − L2/4 . |
Обратите внимание, что учет "неточечности"заряда Q привело к тому, что в знаменателе стоит p
квадрат некоторого "расстояния r2 − L2/4, учитывающего конечную длину стержня L.
Рассмотрим случай, когда расстояние r много больше длины стержня L. В этом пределе, оба заряда можно считать точечными. Действительно, если r L, то из точки нахождения заряда q стержень "выглядит"малым объектом, расззмером которого можно пренебречь. Значит, можно ожидать, что сила взаимодействия должна определяться законом Кулона. Убеждаемся в этом, пренебрегая величиной L2/4 по сравнению с r2 (если, например, r больше L в 10 раз, то r2 превышает L2/4 в 400 раз!):
F = k |
. |
(9) |
|
|
|||
|
r2 |
|
|
|{z}
r L
1.4Задача 4.
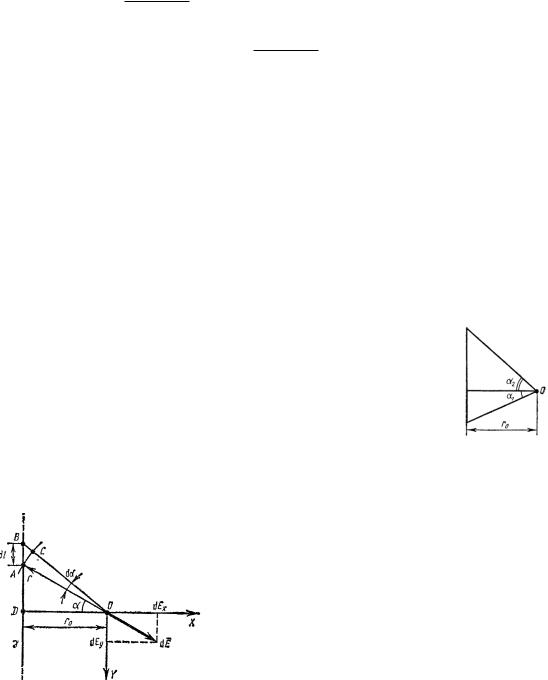
Заряд равномерно распределен по тонкому стержню с линейной плотностью λ (см. предыдущую задачу). Найти напряженность электрического поля в точке O, расположенной на расстоянии r0 от стержня. Углы α1 и α2 заданы (см. рис. 4.1).
Рис. 4.1
Решение.
Как и задаче 3, разбиваем стержень на бесконечно-малые элементы длины dl (обратите внимание на некоторую разницу в обозначениях).
Рассмотрим один такой элемент AB, который виден из точки O под углом α (см. рис. 4.2). Величина напряженности электрического поля, созданного точечным зарядом dQ = λdl в точке O, равна
|
dE = k |
λdl |
|
(10) |
|
r2 |
|||
|
|
|
||
Рис. 4.2 |
Из треугольника ADO находим: r = r0/ cos α. |
|
||
3

Так как |AC| = rdα = r0dα/ cos α, то из треугольника ABC определяем |
|
||||||||||
dl = |
|AC| |
= |
r0dα |
. |
|
|
|
|
|||
|
|
|
|
|
|
||||||
cos α |
cos2 α |
|
|
|
|||||||
Подставляя значения r и dl в уравнение (10), получаем |
|
|
|
||||||||
dE = k |
λdα |
. |
|
|
|
|
|
|
(11) |
||
|
|
|
|
|
|
|
|||||
|
|
r0 |
|
|
|
|
|
|
|
||
Проекции вектора dE на оси OX и OY : |
|
|
|
||||||||
dEx = dE cos α = k |
λ cos αdα |
, dEy = dE sin α = k |
λ sin αdα |
|
(12) |
||||||
|
r0 |
||||||||||
|
|
|
|
|
|
|
r0 |
|
|||
Применяя принцип суперпозиции E (и его проекций), интегрируем оба соотношения из (12) в пределах от α = −α1 (самый нижний элемент стержня) до α = α2 (самый верхний элемент):
α2 |
|
|
λ |
α2 |
|
|
λ |
|
|
|
|
||
Ex = Z−α1 |
dEx = k |
Z−α1 |
cos αdα = k |
|
sin α1 |
+ sin α2 |
|
||||||
|
|
|
|
||||||||||
r0 |
r0 |
||||||||||||
α2 |
|
|
λ |
α2 |
|
λ |
|
|
|
||||
Ey = Z−α1 |
dEy = k |
|
Z−α1 |
sin αdα = k |
cos α1 |
− cos α2 |
|
||||||
|
|
|
|
||||||||||
r0 |
r0 |
||||||||||||
|
Ex = k |
λ |
sin α1 + sin α2 |
|
|
|||
|
r0 |
|
|
|||||
Итак, ответ: |
|
cos α1 − cos α2 |
|
(13) |
||||
|
λ |
|||||||
|
Ey = k |
|
|
|||||
|
r0 |
|
|
|||||
Рассмотрим частные случаи. |
|
|
||||||
• Поле на серединном перпендикуляре. В этом случае α1 = α2 ≡ α. Значит |
|
|||||||
Ex = k |
2λ sin α |
, |
Ey = 0 . |
|
(14) |
|||
|
|
|||||||
|
r0 |
|
|
|
|
|
|
|
•Поле в точках, "лежащих очень близко" к стержню. "Очень близко" означает, что длина стержня L намного превышает расстояние r0. В пределе r0/L → 0 имеем: α1, α2 → π/2. В результате, получаем:
Ex = k |
2λ |
, Ey = 0 . |
(15) |
|
|||
|
r0 |
|
|
Эти выражения определяют электрическое поле бесконечно-длинной нити.
•Поле в точках, "лежащих очень далеко"от стержня, т.е. = L r0.
В этом пределе (см. рис. справа):
|
|
|
|
l1,2 |
|
|
|
l1,2 |
|
|
L1 |
|
α2 |
|||||||
sin α1,2 |
= |
|
|
|
≈ |
, |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
r0 |
|
|
|
|
|
|
|||||||
|
|
2 |
|
2 |
|
. |
|
|
R |
|
||||||||||
cos α1,2 |
= |
|
r |
|
|
+ l |
|
|{z} |
1 + O (l1,2/r0)2 |
L2 |
0 |
α1 |
||||||||
|
|
q |
0r0 |
1,2 |
l1,2 r0 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
r02 + l12,2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
l1,2≈r0 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|{z} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ(l1 + l2) |
|
|
Q |
|
|
|
|
|
|
|
||||||
= Ex = k |
|
|
|
|
= k |
|
|
|
|
|
|
|
|
|||||||
|
|
r02 |
|
r02 |
|
|
|
|
|
|
|
|||||||||
Ey = 0
т.е. получили электрическое поле точечного заряда Q = λ(l1 + l2), как и д.б.
(16)
(17)
4

1.5Задача 5.
Кольцо радиусом R из тонкой проволоки равномерно заряжено с линейной плотностью λ. Определить напряженность поля на оси кольца в точке, удаленной на расстояние r от его центра.
DL
R |
|
|
|
|
α |
DE1 |
E |
O |
R |
DE2 |
|
|
|
||
|
|
|
|
|
|
DE |
|
Разбиваем кольцо на бесконечно-малые элементы. Рассмотрим один такой элемент длины dl, см. рис. Вектор dE на рисунке представляет напряженность электрического поля, созданного зарядом dQ = λdl. Величина этого вектора равна
dE = k |
λdl |
(18) |
|
R2 + r2 |
|||
|
|
Представим этот вектор в виде суммы dE = dE1 + dE2, где dE1 направлен по оси кольца, а dE2 - перпендикулярно ему. Из рисунка видно, что
|
√ |
r |
|
|
√ |
R |
(19) |
|
dE1 = dE cos α = dE |
|
, |
dE2 = dE sin α = dE |
|
. |
|||
R2 + r2 |
R2 + r2 |
|||||||
По принципу суперпозиции, поле E, созданное всем кольцом, равно сумме (интегралу) всех
dE:
I I I
E = dE = dE1 + dE2, (20)
H
где обозначает интеграл по замкнутому контуру (кольцу).
H
Последний интеграл в (20) равен нулю, dE2 = 0. Действительно, для каждого dl можно выбрать диаметрально-противоположный элемента кольца, создающий противоположно на-
правленную составляющую E2. Сладываясь, оба вектора E2 взаимно компенсируются. |
|
|||||||||
В интеграле |
|
dE1 все векторы dE1 сонаправлены, поэтому можно написать dE1 = |
dE1. |
|||||||
|
|
|
результат, формулу (18), а также первое уравнение в (19), записываем ответ: |
|||||||
Используя этот H |
|
|
H |
H |
||||||
E = I |
|
|
|
λr |
I dl = k |
Qr |
(21) |
|||
dE1 = k |
|
|
|
. |
||||||
(R2 + r2)3/2 |
(R2 + r2)3/2 |
|||||||||
|
|
|
|
|
|
|
=2πR |
|
||
Здесь |
Q = 2πRλ |
- заряд кольца. |
Вектор E направлен по оси кольца. |
|
||||||
|
|
|
|{z} |
|
||||||
Частные случаи.
•Поле в центре кольца.
В этом случае r = 0 и, как следствие, E = 0.
•Поле в точках, "лежащих очень далеко"от кольца. "Очень далеко"= r R. В этом пределе:
E = k |
Qr |
≈ k |
Qr |
= k |
Qr |
, |
|
|
|
||||
(R2 + r2)3/2 |
r3 |
r3 |
т.е. получили электрическое поле точечного заряда Q, как и д.б.
5
1.6Задача 6.
Заряд Q равномерно распределен по поверхности тонкого диска3 радиуса R. Определить напряженность поля на оси диска в точке, удаленной на расстояние r от его центра O.
Решение.
Для определенности, полагаем Q > 0.
Заряд Q распределен равномерно, поэтому на единицу площади диска приходится заряд σ = Q/πR2. Величина σ называется поверхностной плотностью заряда, [σ] = Кл/м2.
Чтобы найти напряженность E электрического поля диска, воспользуемся результатом предыдущей задачи. Для этого, представим диск в виде набора бесконечно-тонких (шириной dρ) концентрических (т.е., с общим центром) колец. Одно из таких колец, радиуса ρ (0 ≤ ρ ≤ R) приведено на рисунке.
ρ
 O
O
R
Для определения напряженности электрического поля, создаваемого кольцом, используем последнее равенство в (21), где проделываем следующие замены: (a) Q → dQ = σ2πρdρ (здесь 2πρdρ - площадь бесконечно-тонкого кольца, а dQ - б/малый заряд, расположенный на кольце);
(б) r → ρ, и (в) E → dE. Тогда
dE = k |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(22) |
|||
(ρ2 + r2)3/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Интегрируя по ρ в пределах от 0 до R находим искомую напряженность поля: |
|
||||||||||||||||||||
|
R |
σ2πr ρ dρ |
R |
ρ dρ |
1 − |
|
r |
|
. |
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
E = Z0 |
|
k |
|
|
= 2kπσr Z0 |
|
|
|
|
= 2kσπ |
|
(23) |
|||||||||
|
(ρ2 + r2)3/2 |
(ρ2 + r2)3/2 |
(R2 + r2)1/2 |
||||||||||||||||||
Здесь учтено, что |
ρ (ρ2 + r2)−3/2dρ = −(ρ2 + r2)−1/2. |
|
|
|
: |
|
|
||||||||||||||
В пределе r R |
получаем электрическое поле точечного заряда |
Q |
|
|
|||||||||||||||||
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
R2 |
|
Q |
|
|
|
|
|
|
|||
E = 2kσπ 1 |
− |
|
≈ 2kσπ |
|
= k |
|
|
|
|
|
|
|
(24) |
||||||||
(R2 + r2)1/2 |
2r2 |
r2 |
|
|
|
|
|
||||||||||||||
1.7Задача 7.
Заряд Q равномерно распределен по поверхности сферы радиуса R. Определить напряженность поля в точке, удаленной на расстояние r от центра O сферы.
Решение.
Эту задачу можно решить, используя подход, рассмотренный в предыдущих задачах. т.е. представить весь заряд поверхности как совокупность б/малых зарядов dQ = σdS (где dS элемент площади), для каждого из которых определить dE, и, затем применить принцип суперпозиции для нахождения полной напряженности E. Этот подход применим всегда, однако, он может сопровождаться сложным интегрированием (аналитическим или численным).
Нахождение напряженности электрического поля, созданного заряженными системами обладающими определенной симметрией, бывает эффективнее провести с использованием теоремы Гаусса. Теорема Гаусса утверждает, что поток вектора E через произвольную замкнутую
3"Тонкий диск"= его толщиной можно пренебречь.
6
поверхность Σ равен электрическому заряду QΣ, заключенному внутри этой поверхности, деленному на электрическую постоянную ε0:
IΣ E · dS = |
QΣ |
(25) |
ε0 . |
| {z }
поток E через Σ
H
Здесь Σ обозначает интеграл по замкнутой поверхности. Вектор dS направлен по нормали (изнутри наружу) к элементу поверхности.
Применение теоремы Гаусса основано на использовании свойств симметрии системы (а следовотельно, и создаваемого ею электрического поля) для выбора поверхности Σ.
Равномерно заряженная сфера является примером системы обладающей сферической симметрией. Сфера переходит сама в себя при любом повороте относительно любой оси, проходящей через ее центр, а также при зеркальном отражении относительно любой плоскости, проходящей через центр.
Такими же свойствами симметрии обладает и электрическое поле E, создаваемое сферой. Можно утверждать, что
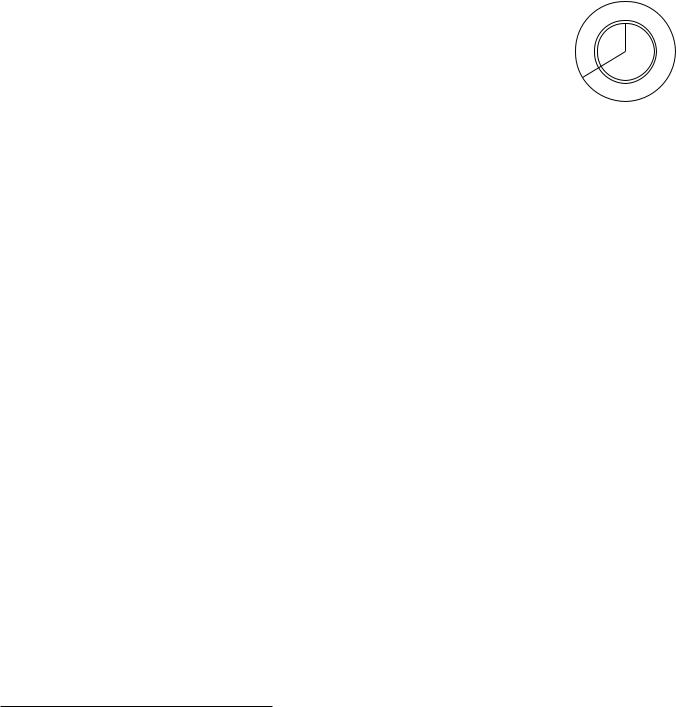
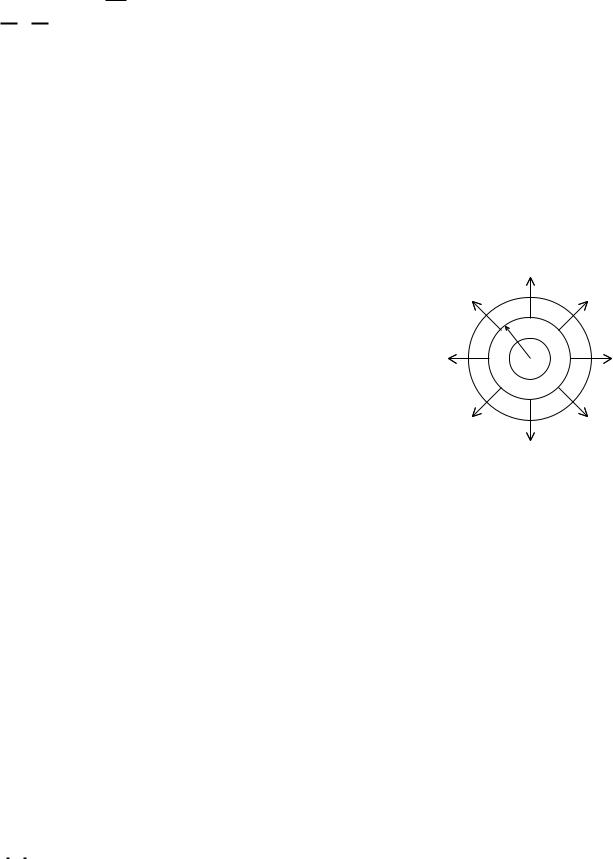
(a)В любой точке пространства, характеризуемой радиусвектором r, вектор E коллинеарен с r. Иными словами, силовые линии E представляют собой лучи, сходящиеся к центру (если Q < 0) или расходящиеся от центра (если Q > 0) сферы (см. рис.).
(b)Во всех точках пространства, лежащих на одинаковом удалении r от центра (т.е. на сферической поверхности r = const), величина E напряженности поля одинакова.
|
R>R |
|
+ |
+ |
|
R |
+ |
|
+ |
||
σ |
||
|
||
+ |
+ |
|
|
R<R |
++
Для вычисления интеграла из (25) в качестве замкнутой поверхности Σ выберем сферу радиуса r, имеющую общий центр с заряженной сферой (для определенности считаем, что заряд Q положительный). Тогда, учитывая, что в любом месте сферы r векторы E и S сонаправлены (свойство (a)), и величина E одинакова во всех точках сферы r (свойство (b)), вычисляем поток
вектора E через Σ: |
|
|
|
|
|
|
|
IΣ E · dS = IΣ EdS = E |
IΣ dS |
4πr2E . |
(26) |
||||
|
| |
|
{z |
|
} |
|
|
площадь сферы
Правая часть уравнения (25) принимает различные значения в зависимости от того, где ищется поле E: снаружи заряженной сферы (r > R) или внитри неё (r < R).
•Если r > R, то весь заряд Q находится внутри замкнутой поверхности Σ, т.е. QΣ = Q.
•Если r < R, то внутри Σ зарядов нет, и = QΣ = Q.
Таким образом, мы установили, что величина электрического поля E, создаваемого заря-
женной сферой на расстоянии r равна |
|
||||||
|
1 |
|
|
Q |
|
|
|
|
|
|
|
|
|
||
E = |
|
×( r2 |
вне сферы, r > R |
(27) |
|||
|
|
|
|||||
|
4πε0 |
||||||
|
| {z } |
0 |
внутри сферы, r < R |
|
|||
|
|
|
|
|
|||
=k
7
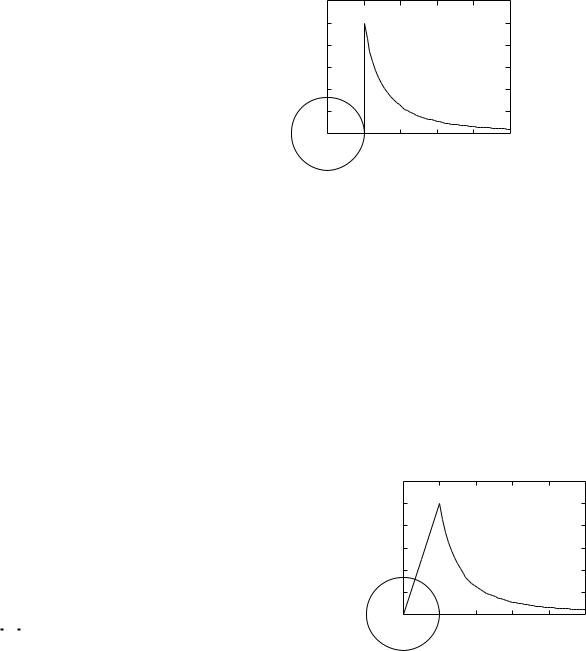
Таким образом, внутри заряженной сферы электрическое поле отсутствует, а снаружи оно совпадает с электрическим полем точечного заряда Q, помещенного в центр сферы.
E |
|
|
|
|
E 1/R2 |
|
|
|
|
R=R |
2R |
3R |
4R |
R |
|
|
|
|
|
1.8Задача 8.
Заряд Q равномерно распределен по объёму шара радиуса R. Определить напряженность поля в точке, удаленной на расстояние r от центра O сферы.
Решение.
Распределение заряда по объему характеризуется объемной плотностью ρ, которая имеет смысл заряда, приходящегося на единицу обЪёма ([ρ] = Кл/м3). При равномерном распределении, объемной плотностью одинакова в любой точке шара и равна ρ = Q/V , где V = 4πR3/3.
Решение этой задачи аналогично предыдущей. Поток вектора E даётся формулой (26). Если r > R (поле вне шара), то как и ранее весь заряд Q находится внутри замкнутой
поверхности Σ, и = QΣ = Q.
Отличие возникает для r < R. В этом случае, QΣ равно заряду внутри сферы радиуса r: QΣ = ρ4πr3/3. Подставляя это значение в правую часть уравнения (25) и приравнивая результат потоку из (26), получаем
E = |
1 |
ρ |
r |
= |
1 3Q r |
= k |
Q |
r . |
||||
|
|
|
|
|
|
|
|
|||||
ε0 |
3 |
ε0 4πR3 3 |
R3 |
|||||||||
Таким образом, окончательный ответ гласит:
|
1 |
|
< |
Q |
r > R |
||||
|
|
|
|
|
|
||||
|
|
|
3 |
|
|||||
E = |
|
8 r2 |
|||||||
|
|
|
|
||||||
|
|
4πε0 |
×> |
Q |
r |
r < R |
|||
|
|
|
|||||||
|
| {z } |
: |
|
|
|
|
|
||
|
|
=k |
> R |
|
|
|
|
||
(28)
(29)
E |
|
|
|
|
E 1/R2 |
|
|
|
|
E R |
|
|
|
|
R=R |
2R |
3R |
4R |
R |
|
|
|
|
|
Итак, напряженность поля вне равномерно заряженного шара совпадает с полем точечного заряда, а внутри шара растет линейно с расстоянием r, см. рисунок.
1.9Задача 9.
Найти напряженность электрического поля бесконечной тонкой нити на расстоянии r от неё. Нить заряжена равномерно с линейнои плотностью λ > 0.
Решение.
8

Для использования теоремы Гаусса, в качестве замкнутой поверхности Σ выберем цилиндр радиуса r и высотой l, ось которого совпадает с нитью (т.н. коаксиальный (соосный) цилиндр).
Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра.
Поток вектора E сквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность 2πrl E.
Заряд QΣ, находящийся внутри цилиндра, равен λl.
Используя эти результаты в (25), получаем:
E = |
1 |
|
λ |
. |
(30) |
|
|
||||
|
2πε0 r |
|
|||
Этот результат совпадает с формулой (15), полученной другим способом.
9
