Добавил:

Syrupotkashlya Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный морской технический университет

Предмет:

Физика

Файл:

Лекция 6

.pdf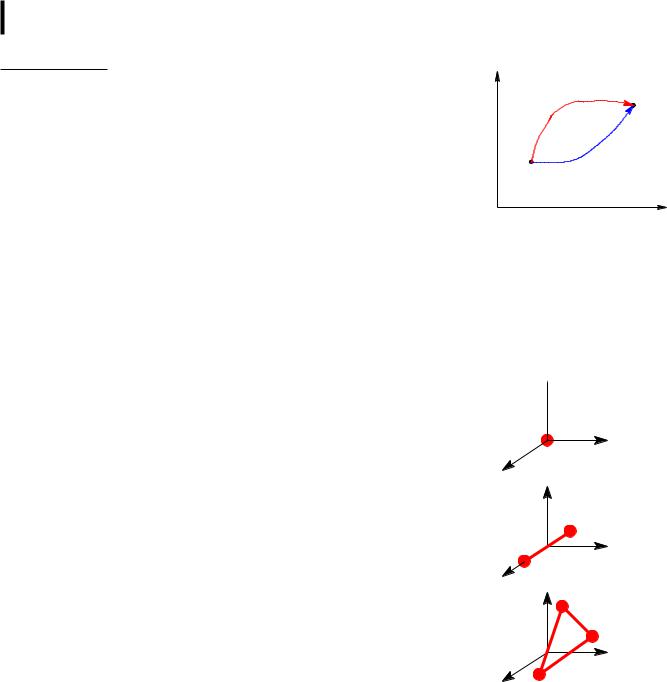

Скачиваний:

Добавлен:

20.12.2023

Размер:

271.72 Кб

Скачать

☆

Лекция 6 Основы термодинамики

6.1Внутренняя энергия

Любая т/д система характеризуется внутренней энергией U:

U= энергия хаотического движения молекул + энергия взаимодействия молекул

Квнутренней энергии не относятся: кинетическая энергия движения тела как целого и его потенциальная энергия во внешних полях.

Внутренняя энергия – функция т/д состояния системы, т.е. в каждом состоянии система обладает определенной U.

	Следовательно:
	U не зависит от того, каким образом система пришла в дан-	P
	U не зависит от того, каким образом система пришла в дан-	2
	ное состояние;	2

При переходе системы из одного состояния ("1") в другое
состояния ("2") изменение внутренней энергии определяется
только разностью значений внутренней энергии этих состояний	1
и не зависит от пути перехода:
∆U = U2 U1:	V

6.2Число степеней свободы

Число ст. св. = числу координат, определяющих положение системы = числу независимых движений системы

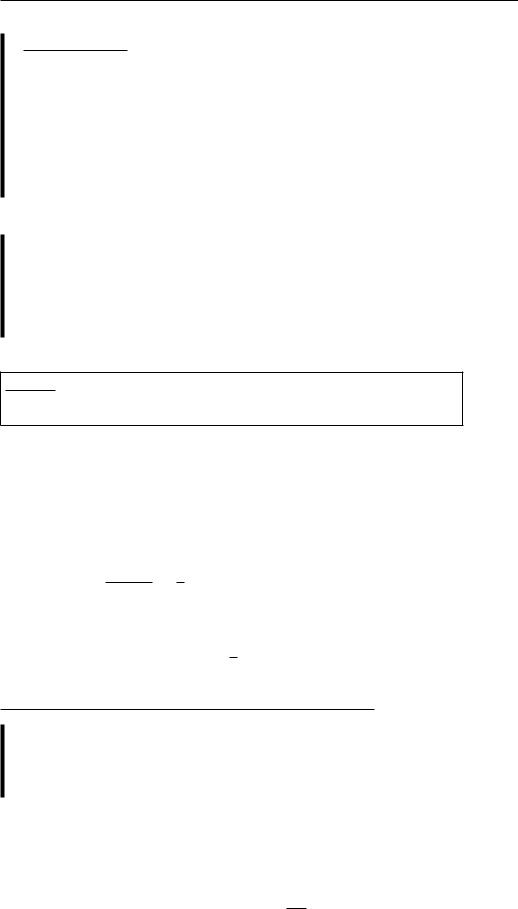
(a)Молекула одноатомного газа материальная точка (3 координаты: (x; y; z)).

=) 3 ст. св. поступательного движения (вдоль X; Y; Z).

(b)Молекула двухатомного газа 2 материальных точки (6 координат: (xj; yj; zj) где j = 1; 2).

=) 6 ст. св. = 3 ст. св. поступательного движения

+2 ст. св. вращательного движения

+1 ст. св. колебательного движения

Z (a)

(b)

=) 9 ст. св. = 3 ст. св. поступательного движения

+3 ст. св. вращательного движения

+3 ст. св. колебательного движения

(c)

А.В. Король. "Молекулярная физика и термодинамика". Лекция 6 41

Общий случай – n-атомная молекула

число ст. св. = 3n = iпост +iвращ + iкол

|{z}

				8		=3
				8	0	для n = 1;
				<	0	для n = 1;
где	i	вращ	=		2	для n = 2;
где		вращ			3	для n 3:

n	iвращ:
iкол = 3: iпост

Для жёстких молекул колебательным движением пренебрегается:

=) число ст. св. жёстких молекул = iпост + iвращ:

Для многих газов колебательными степенями свободы можно пренебречь вплоть до температур T 103 K.

(Объяснение этого явления даётся в рамках квантовой механики.)

Пример: Найти число степеней свободы молекулы спирта C2H5OH.

Число атомов: n = 9. =) число ст. св. = 3n = 27.

Из них: iпост = 3, iвращ = 3, iкол = 27 6 = 21.

6.3Закон Больцмана о равномерном распределении энергии по степеням свободы

Ранее получали связь средней энергии поступательного движения с температурой (см. Лекцию 5):

"пост m0 v2 = 3kT:

2 2

Поскольку ни одна из поступательных степеней свободы не имеет преимущества, то

vx2 = vy2 = vz2 =)	1
	2kT = средней энергии каждой пост. ст. своб.

Более общее утверждение (можно строго доказать):

Закон Больцмана о равномерном распределении энергии по ст. св.:

для системы, находящейся в состоянии т/д равновесия, на каждую поступательную и вращательную степени свободы приходится (в среднем) кинетическая энергия, равная kT=2, а на каждую колебательную степень свободы – энергия, равная kT .

Колебательная степень обладает вдвое большей энергией, т.к. на нее приходится не только кинетическая энергия, но и потенциальная (т.к. атомы внутри молекулы взаимодействуют), причем

кин. энергия = пот. энергия = kT2

А.В. Король. "Молекулярная физика и термодинамика". Лекция 6 42

Таким образом, средняя энергия движения молекулы

"пост

iпост

iвращ2

"вращ

= "

пост

+ "

вращ

+ "

кол

kT;

где

кол

= i

кол

i = iпост +iвращ + 2iкол:

Для жестких молекул

кол

= 0 = i = i

пост

+ i

|{z}

)

вращ.

В идеальном газе потенциальная энергия взаимодействия молекул равна нулю, поэтому
внутренняя энергия газа, содержащего N частиц, определяется средней энергией дви-
жения его молекул:
i	N i	m i	i	(6.1)
U = N " = N 2 kT =	NA 2RT =	2RT =	2 RT:	(6.1)

6.4 Первое начало термодинамики

I-е начало термодинамики – это закон сохранения и превращения энергии в термодинамических процессах.

Внутреннюю энергию системы можно изменить двумя способами:

(1) Совершая над системой работу

(напр., сжимая газ в цилиндре с помощью поршня увеличиваем T и, =), U);

(2) Сообщая системе теплоту

(напр., нагревая газ в герметичном сосуде).

Рассмотрим произвольную замкнутую, макроскопически	P
Рассмотрим произвольную замкнутую, макроскопически		COCT. 2
неподвижную систему, не находящуюся во внешних сило-		COCT. 2
неподвижную систему, не находящуюся во внешних сило-		(U2)
вых полях и проанализируем с энергетической точки зре-
ния равновесный процесс перехода системы из какого-либо		COCT. 1
начального состояния 1 (с внутренней энергией U1), в дру-		COCT. 1
начального состояния 1 (с внутренней энергией U1), в дру-		(U1)
гое состояние 2 (с внутренней энергией U2).
гое состояние 2 (с внутренней энергией U2).		V
		V
Опыт показывает:
Изменение внутренней энергии системы ∆U = U2 U1	в таком процессе равно разности
между количеством теплоты Q, полученным системой, и работой A, совершенной системой
против внешних сил ∆U = Q A или Q = ∆U + A.

I-е начало термодинамики: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил: Q = ∆U +A.

А.В. Король. "Молекулярная физика и термодинамика". Лекция 6 43

I-е начало термодинамики в дифференциальной форме: Q = A + dU.

Здесь: dU (полный дифференциал) - бесконечно малое изменение внутренней энергии системы, A – элементарная (бесконечно малая) работа, Q – бесконечно малое количество теплоты.

A и Q не являются полными дифференциалами.

Дело в том, что внутренняя энергия системы является однозначной функцией состояния системы. Отсюда следует, что при совершении системой произвольного процесса,

в	результате которого она совершает переход Сост1								!		Сост2, изменение внутренней энергии
				2
∆U =				1 dU сводится к разности U2	U1 значений вн. энергии в конце и начале процесса.
Т.о.,		величина ∆U не зависит от способа перехода из Сост1 в Сост2
			∫			12 A и теплота Q = 12 Q являются функция-
Напротив, совершаемая работа A =
ми процесса					Сост1		!	Сост2		. Как следтствие, A и Q не могут быть
				, т.е. способа перехода	∫						∫

представлены в виде разностей каких-то значений, соответствущих начальному и конечному состояниям.

Все величины входящие в первое начало термодинамики могут быть как положительными, так и отрицательными:

Если к системе подводится теплота, то Q > 0; если теплота отводится, то Q < 0.

Если система совершает работу над внешними телами, то A > 0, если же внешние силы совершают работу над системой, то A < 0.

Если система, совершая процесс возвращается в начальное состояние (т.н. круговой процесс), то ∆U = 0. Следовательно, в круговом процессе Q = A.

Отсюда следует невозможность вечного двигателя I-го рода: невозможен периодически действующего двигатель, совершающего б´ольшую работу, чем сообщенная ему извне теплота: A > Q.

6.5	Работа газа
Найдем работу, совершаемую газом при изменении его объема.			S
		P
Пример: газ, находящийся под поршнем в цилиндрическом сосуде.			dl
			dl
Расширяясь, газ передвигает поршень на расстояние dl, и про-		P
изводит элементарную работу		P
	A = F dl = P Sdl = P dV:
Полная работа, совершаемая газом при V1 ! V2:		dA=PdV
	V	dA=PdV
	V
	A = ∫V1 2 P dV:	V	dV	V	V
Результат интегрирования определяется характером зависимости P (V ).		1		2	V

Графически, абсолютное значение jAj работы совершаемой при V1			! V2	равно

А.В. Король. "Молекулярная физика и термодинамика". Лекция 6 44

площади под кривой P = P (V ) ограниченной участком от V = V1 до V = V2.

{

При этом:

A > 0 если V1 < V2 (расширение)

A < 0 если V1 > V2 (сжатие)

6.6Теплоемкость

Теплоемкость C = отношение количества тепла Q, полученного телом, к соответствующему приращению dT его температуры:

С= dQT ; [C] = Дж/К:

Удельная теплоемкость Cу = количеству теплоты, необходимому для нагревания 1 кг вещества на ∆T = 1К:

1 Q

Cу = m dT ; [Cу] = Дж/(кг К):

Молярная теплоемкость C = количеству теплоты, необходимому для нагревания 1 моля вещества на ∆T = 1К:

C =	1 Q	[C ] = Дж/(моль К):

	dT

Связь молярной и удельной теплоёмкостей: C = Су.

Везде далее рассматривается молярная теплоемкость для 1-го моля: = 1. Индекс у C опускаетсятся.

Теплоемкость зависит от процесса, происходящего с телом.

Наиболее часто используемые теплоемкости:

CV – теплоемкость при постоянном объеме (т.е. в изохорическом процессе); CP – теплоемкость при постоянном давлении ( в изобарическом, процессе).

6.6.1Вычисление CV и CP для идеального газа

Используя понятие теплоемкости, запишем I-е начало термодинамики в виде:

CdT = Q = A + dU:

Рассмотрим это равенство при V = const и P = const

Если V = const, то A = pdV = 0 и Q = dU. Учитывая, что U = iRT=2 (см. ф. (6.1)),

получаем:

CV =

V =const

где i = iпост +iвращ + 2iкол:

Если P =

, то

|{z}

const

pdV

CP = dT

= CV + R

P =const

}

т.к.

iR=2=C

pdV =RdT

А.В. Король. "Молекулярная физика и термодинамика". Лекция 6 45

Следовательно:

CP = CV + R – уравнение Майера.

Неравенство CP > CV справедливо для любых тел. Его смысл: дополнительное тепло при P = const идет на совершение работы при расширении.

Отношение теплоёмкостей CP =CV = называется показателем адиабаты (или, коэффициентом Пуассона).

		i				CP		i + 2
Для идеального газа:	CV =		R	=	=		=		:
		2

{	CP = CV + R			)		CV		i

При T 103 K колебательными степенями свободы можно пренебречь. Поэтому, для жестких молекул:

(a) для одноатомного газа:	i = 3	=)	= 5=3;
(b) для 2-x–атомного газа:	i = 5	=)	= 7=5;
(c) для 3-x-атомного газа:	i = 6	=)	= 8=6:

6.6.2Зависимость теплоемкости от температуры

Проведенное выше рассмотрение предсказывает:

CV = 2i R — не зависит от T !!

Однако, эксперимент показывает, что CV												# при T #.
Например, для 2-x атомной молекулы (i = 3 + 2 + 2 1 = 7),
вместо CV = 7R=2 получается:													7	R
		iпост					3					2		R
												2
T 10 K :
	CV =			R =				R					5	R
		2					2						5
		2					2						2
2		iпост + iкол								5		3
T 10 K :	CV =								R =		R			R

				2						2			2
T 103 K :		i		7
	CV =		R =			R
	CV =	2	R =		2	R

CV
50	500	5000	T (K)

т.е. происходит "замораживание" колебательных (при T 103 K) и вращательных (при T 102 K) степеней свободы.

Объяснение такому поведению CV (T ) можно дать только в рамках квантовой теории.

6.7Применение I-го начала термодинамики к изопроцессам

Изопроцесс – равновесный процесс, при котором один из основных параметров состояния сохраняется постоянным.

А.В. Король. "Молекулярная физика и термодинамика". Лекция 6 46

6.7.1Изохорный процесс, V = const

P –V диаграмма процесса – изохора — прямая ? оси V . dV = 0 =) A = P dV = 0.

Применяя I-е начало термодинамики:

Q = dU = CV dT

=) Q = ∆U = CV (|T2 {z T1}) = CV ∆T

=∆T

(a)

V V

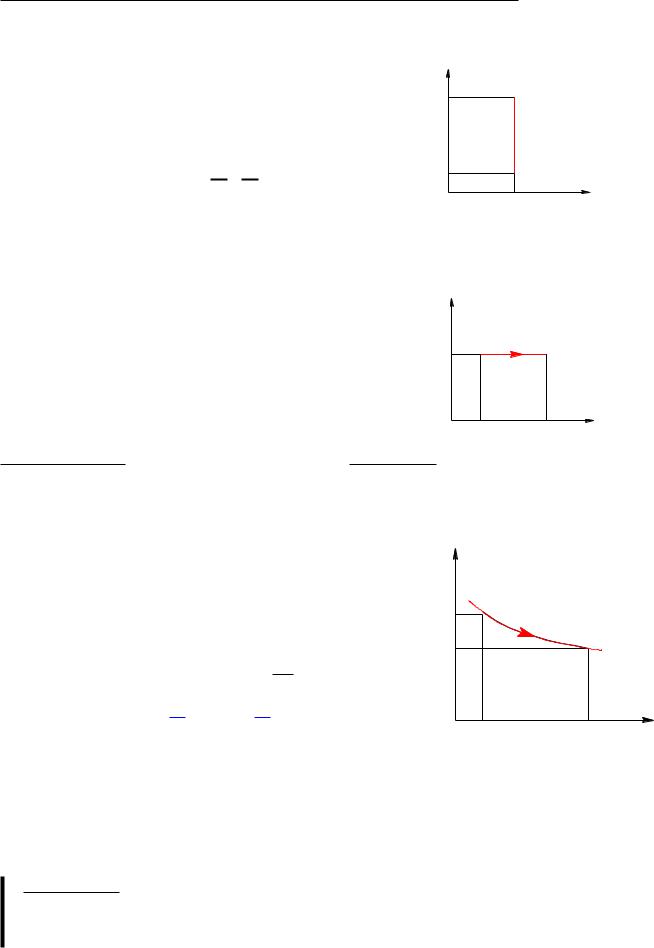
6.7.2 Изобарный процесс, P = const

P V диаграмма – изобара – прямая ? оси P . Используя P V = RT , находим:

∆U = CV ∆T

A = ∫V1

2 pdV = p (

V2 V1)= R ∆T

=∆V

)

| {z

}

∆T

= Q = A + C

∆T = (R + C ) ∆T = C

}

={zP

(b)

V	V	V
1	2	V

При расширении: нагревание (∆T > 0) и A > 0, при сжатии: охлаждение (∆T < 0) и A < 0.

6.7.3Изотермический процесс, T = const

PV диаграмма – изотерма – гипербола P / 1=V .

dT = 0 =) dU = CV dT = 0					P		(c)
dT = 0 =) dU = CV dT = 0
=) Q = A =) Q = A					P
					P
Теплота и работа:					1
Теплота и работа:
	V2		V2	V	P
	V2		V2	V	2
Q = A =	∫V1	pdV = RT	∫V1	dV		A
= RT lnV2 = RT lnP1 :
		V1	P2		V	V	V
					1	2	V
При расширении A > 0, при сжатии A < 0.

6.8Адиабатический процесс

Адиабатический процесс – процесс, в котором отсутствует теплообмен ( Q = 0)

между системой и окружающей средой.

В реальности, должно выполняться неравенство:

∆t

∆t – длительность процесса,

– характерное время, необходимое для теплообмена.

А.В. Король. "Молекулярная физика и термодинамика". Лекция 6 47

Уравнение адиабатического процесса
Применяя I-е начало термодинамики:
					=)	iR
dU + A = 0							dT = P dV
						2
Используя ур-ие Менделеева-Клапейрона, можно получить:
	dP			dV	=) P V = const – ур-ие адиаб. проц.
		=
	P			V
= CP =CV			> 1 – показатель адиабаты (коэффициент Пуассона).

Эквивалентные	формы записи ур-ия адиабатического процесса:
P V = const	=) T V 1 = const	=) P 1 T = const
	RT=V	V = RT=P
	P =\|{z}	\|{z}

P V диаграмма адиабатического процесса (= aдиабата)

P V = const =) P / V1 — адиабата

Адиабата идет круче изотермы (P / 1=V ) т.к. > 1.

Это объясняется тем, что при адиабатическом сжатии увеличение P газа обусловлено не только уменьшением его V , но и повышением T .

Работа при адиабатическом изменении объема.

Из I-го начала термодинамики: A =				dU =			RdT
	P	V1			V1		1
=) A = R(T2 T1) =	1		[1	(		)	]
		1			V2

P
	T=CONST => P 1/V
	P 1/Vγ
P1
P2
V1	V2	V
Сплошная линия — адиабата

Последнее равенство получено с использованием ур-ия адиабатического процесса.

А.В. Король. "Молекулярная физика и термодинамика". Лекция 6 48

6.9Политропный процесс

Политропным называется процесс, в котором теплоемкость C остается постоянной.

Исходя из I-е начала термодинамики можно вывести уравнение политропы, т.е. взаимосвязь давления и объёма газа в политропическом процессе:

P V n = const; где	n =	C	CP	– показатель политропы.

		C	CV

Рассмотренные выше изохорный, изобарный, изотермический и адиабатический процессы – это частные случаи политропного процесса.

При C = 0 получаем n = (=) политропа = адиабата);

При C = 1 получаем n = 1 (=) политропа = изотерма);

При C = CP получаем n = 0 (=) политропа = изобара);

При C = CV получаем n = 1 (=) политропа = изохора).

Литература: Т. И. Трофимова. "Курс Физики’, §§ 50-55.

Соседние файлы в папке Лекции Король А. В.

#
20.12.2023191.74 Кб0Лекция 11.pdf
#
20.12.2023155.59 Кб0Лекция 12.pdf
#
20.12.20231.64 Mб0Лекция 2.pdf
#
20.12.2023250.36 Кб0Лекция 3.pdf
#
20.12.2023261.05 Кб0Лекция 5.pdf
#
20.12.2023271.72 Кб0Лекция 6.pdf
#
20.12.2023220.19 Кб0Лекция 8.pdf
#
20.12.2023173.79 Кб0Лекция 9.pdf