
Информатика. Практика / MetEx2007_Lab8
.docMS Excel 2007 Практ. раб. 8
-
Решение задач оптимизации средствами Microsoft Excel
Для решения задач оптимизации в Microsoft Excel предназначена надстройка Поиск решения.
Постановка задачи
В общем виде задача оптимизации ставится следующим образом: найти оптимальное (максимальное или минимальное) значение функции
![]()
при ограничениях
![]() .
.
Если функции
![]() и
и
![]() являются линейными, т. е.
являются линейными, т. е.
![]()
![]() ,
,
то такая задача называется задачей линейного программирования.
Подготовка блока данных
На рабочем
листе отвести блок данных под изменяемые
ячейки, т. е. ячейки для хранения
переменных
![]() .
В результате решения задачи в этих
ячейках появятся искомые значения
.
В результате решения задачи в этих
ячейках появятся искомые значения
![]() .
.
В отдельную
ячейку ввести формулу для целевой
функции
![]() .
Эта ячейка называется целевой.
.
Эта ячейка называется целевой.
отдельные
ячейки ввести формулы для левой части
ограничений
![]() .
.
Запуск программы «Поиск решения»
-
На вкладке Данные в группе Анализ выбрать команду Поиск решения.
-
В поле Установить целевую ячейку ввести ссылку на целевую ячейку.
-
В поле Изменяя ячейки ввести ссылку на диапазон изменяемых ячеек.
-
Для задания ограничений в группе Ограничения щелкнуть по кнопке Добавить.
В открывшемся диалоговом окне выполнить следующие действия:
-
в поле Ссылка на ячейку ввести ссылку на ячейку с формулой, определяющей первое ограничение (
 );
); -
во втором поле выбрать оператор ограничения (>, <, = и т.д);
-
в поле Ограничение ввести значение ограничения
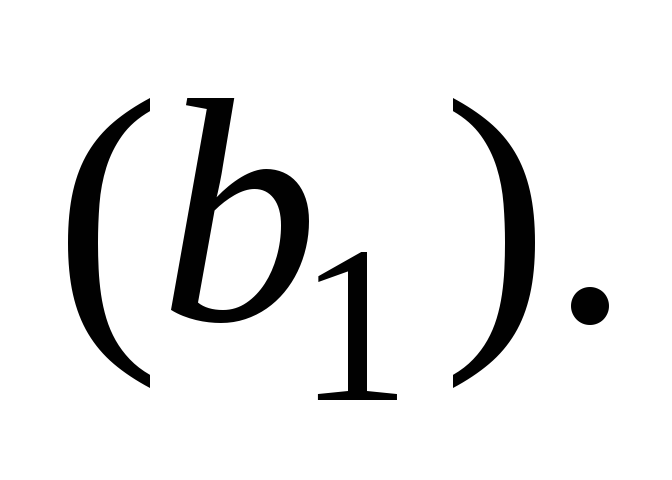
-
Для задания следующего ограничения щелкнуть по кнопке Добавить и повторить операции пункта 4.
-
Когда все ограничения будут заданы, щелкнуть по кнопке ОК, чтобы вернуться в диалоговое окно Поиск решения.
-
Изменять и удалять ограничения можно с помощью кнопок Изменить и Удалить.
-
При необходимости можно задать максимальное время решения, предельное число итераций, относительную погрешность, допустимое отклонение, сходимость, метод поиска. Для этого с помощью кнопки Параметры открыть диалоговое окно Параметры поиска решения.
Если известно, что решаемая задача линейная, то следует включить режим Линейная модель: процесс решения значительно ускорится.
Для возврата в диалоговое окно Поиск решения щелкнуть по кнопке ОК.
-
Для инициализации процедуры поиска решения щелкнуть по кнопке Выполнить.
Полученные результаты будут выведены на рабочий лист.
После завершения процедуры решения в диалоговом окне Результаты поиска решения можно выполнить один из следующих вариантов:
-
сохранить найденное решение или восстановить исходные значения на рабочем листе;
-
сохранить параметры поиска решения в виде модели;
-
сохранить решение в виде сценария;
-
просмотреть любой из встроенных отчетов.
Сохранение модели
Текущие установочные параметры для поиска решения можно сохранить в виде модели.
Для этого надо в диалоговом окне Параметры поиска решения щелкнуть по кнопке Сохранить модель и указать на рабочем листе область для сохранения модели (можно указать только верхнюю ячейку области).
При сохранении модели запоминаются целевая ячейка, изменяемые ячейки, ограничения и параметры поиска решения.
Чтобы впоследствии загрузить модель, надо щелкнуть по кнопке Загрузить модель в диалоговом окне Параметры поиска решения.
Сохранение сценария
Найденные решения (значения изменяемых ячеек) можно сохранить в качестве сценария. Для этого нужно:
-
В диалоговом окне Результаты поиска решения выбрать Сохранить сценарий.
-
В поле Название сценария ввести имя.
Просмотреть сценарии можно с помощью команды Диспетчера сценариев (на вкладке Данные в группе Работа с данными в списке Анализ «что-если» выбрать команду Диспетчер сценариев).
Создания отчета по результатам поиска решения
С помощью программы Поиск решения можно создать три типа отчетов по результатам, полученным при успешном завершении процедуры решения. Каждый отчет создается на отдельном листе текущей рабочей книги.
Для создания отчета надо в диалоговом окне Результаты поиска решения выбрать нужный тип в поле Тип отчета. Можно выбрать сразу несколько типов (при выделении нескольких строк используется клавиша Ctrl).
Типы отчетов:
-
результаты – отчет содержит целевую ячейку, список изменяемых ячеек, их исходные и конечные значения, ограничения и сведения о них;
-
устойчивость – отчет содержит сведения о степени зависимости модели от изменений величин, входящих в формулы, применяемые в задаче (формулы модели и формулы ограничений);
-
пределы – выводится целевая ячейка и ее значение, а также список изменяемых ячеек, их значений, нижних и верхних пределов и целевых результатов.
Практическая работа 8
Решение задач оптимизации средствами Microsoft Excel
-
Решить задачи линейного программирования:
-
найти максимальное значение функции
![]()
при следующих
ограничениях:

Ответ:
![]() при
при
![]()
-
найти минимальное значение функции
![]()
при следующих
ограничениях:

Ответ:
![]() при
при
![]()
-
Решить задачи нелинейного программирования:
-
найти максимальное значение функции
 при условии
при условии

Ответ:
![]() при
при
![]() ;
;
-
найти максимальное и минимальное значение функции
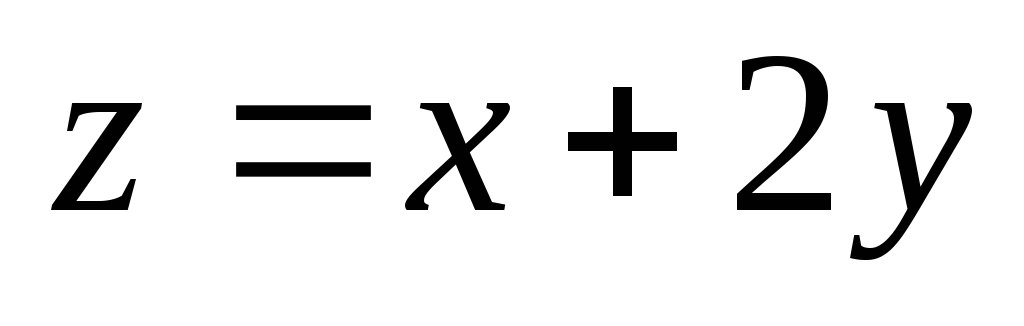 при условии
при условии
 .
.
Ответ:
![]() при
при
![]() ;
;
![]() при
при
![]() ;
;
-
найти максимальное и минимальное значение функции
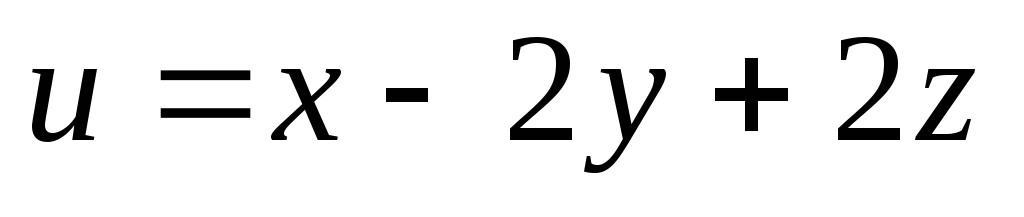 при условии
при условии
 .
.
Ответ:
![]() при
при
![]()
![]() при
при
![]()
-
найти максимальное значение функции
 при условиях
при условиях
 и
и
 .
.
Ответ:
![]() при
при
![]() .
.
-
Найти оптимальное решение следующих экономических задач:
-
Задача планирования производства
Фирма реализует товары двух видов: Товар 1 и Товар 2, используя при этом четыре типа ресурсов – технические, трудовые, финансовые и транспортные. Норма затрат ресурсов на единицу товара, общий объем каждого ресурса и прибыль от реализации каждого товара заданы в таблице 1.
Таблица 1
|
Ресурсы |
Норма затрат ресурсов на товары |
Общее количество ресурсов |
|
|
Товар 1 |
Товар 2 |
||
|
Технические |
2 |
2 |
12 |
|
Трудовые |
1 |
2 |
8 |
|
Финансовые |
4 |
0 |
16 |
|
Транспортные |
0 |
4 |
12 |
|
Прибыль на единицу продукции, руб. |
2,00 |
3,00 |
|
Требуется определить количество товаров каждого вида, обеспечивающее фирме максимальную прибыль.
В этой задаче переменные
![]() и
и
![]() – количество товаров каждого вида;
целевая функция
– количество товаров каждого вида;
целевая функция
![]() ;
;
ограничения на объем
каждого вида ресурсов:
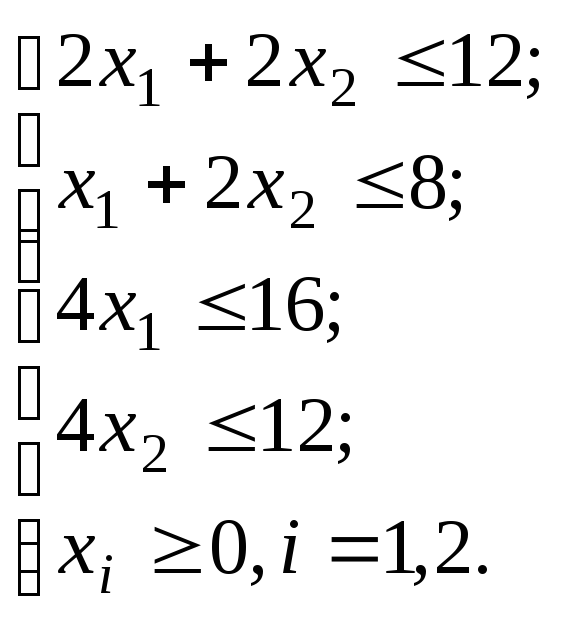
Ответ:![]()
-
Транспортная задача
Предприятия, выпускающие одинаковую продукцию, могут реализовать ее в трех различных магазинах. Стоимость транспортировки единицы объема продукции от каждого предприятия до каждого магазина, а также объем готовой продукции на каждом предприятии и пропускная способность каждого магазина приведены в таблице 2.
Таблица 2
|
|
Магазин 1 |
Магазин 2 |
Магазин 3 |
Магазин 4 |
Объем готовой продукции |
|
Предприятие 1 |
2 |
4 |
3 |
5 |
1 000 |
|
Предприятие 2 |
7 |
6 |
4 |
3 |
1 100 |
|
Предприятие 3 |
2 |
5 |
5 |
7 |
900 |
|
Пропускная возможность магазинов |
500 |
1 100 |
700 |
700 |
|
Рассчитать объем продукции, который следует поставлять с каждого предприятия в каждый магазин, чтобы затраты по транспортировке были наименьшими.
Здесь переменные
![]() − объем продукции, поставляемый из i-го
предприятия в j-й
магазин; целевая функция
− объем продукции, поставляемый из i-го
предприятия в j-й
магазин; целевая функция
 ограничения
на объем готовой продукции:
ограничения
на объем готовой продукции:

ограничения,
накладываемые пропускной возможностью
магазинов:

кроме того
![]()
![]() ‑ ограничения, определяемые физическим
смыслом задачи.
‑ ограничения, определяемые физическим
смыслом задачи.
Ответ:
