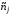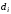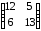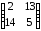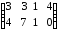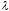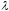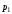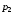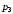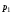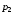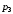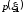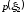КР_теория_игр
..docxКонтрольная работа №1
Задача №1.1
На
каждой из двух торговых баз ассортиментный
минимум составляет один и тот же набор
из n
видов товаров. Каждая база должна
поставить в свой магазин только один
из этих видов товара. Магазины А и В
конкурируют между собой. Один и тот же
вид товара в обоих магазинах продается
по одной и той же цене. Однако, товар,
поставляемый в магазин В, более высокого
качества. Если магазин А завезет с базы
товар
i-го
вида (i=1,…
,n),
отличный от товара
j-го
вида (j=1,..,n),
завезенного в магазин В, то товар i-го
вида будет пользоваться спросом и
магазин А от его реализации получит
прибыль
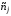 денежных единиц. Если же в магазины А и
В завезены товары одинакового вида i=j,
то товар i-го
вида в магазине А спросом пользоваться
не будет , поскольку, такой же товар, по
такой же цене, но более высокого качества,
можно купить в магазине В, и по этому
магазин А понесет убытки при транспортировке,
хранению и возможно порче товара
i-го
вида в размере
денежных единиц. Если же в магазины А и
В завезены товары одинакового вида i=j,
то товар i-го
вида в магазине А спросом пользоваться
не будет , поскольку, такой же товар, по
такой же цене, но более высокого качества,
можно купить в магазине В, и по этому
магазин А понесет убытки при транспортировке,
хранению и возможно порче товара
i-го
вида в размере
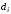 денежных единиц. Описать данную ситуацию
методами теории игр, составить матрицу
игры. Данные соответствующие вашему
варианту брать в таблице 1.1
денежных единиц. Описать данную ситуацию
методами теории игр, составить матрицу
игры. Данные соответствующие вашему
варианту брать в таблице 1.1
Таблица 1.1
|
Вариант |
n |
|
|
|
1 |
3 |
20 |
10 |
|
2 |
4 |
30 |
15 |
|
3 |
5 |
25 |
30 |
|
4 |
3 |
16 |
10 |
|
5 |
4 |
50 |
35 |
|
6 |
5 |
37 |
24 |
|
7 |
3 |
51 |
33 |
|
8 |
4 |
28 |
18 |
|
9 |
5 |
55 |
48 |
|
10 |
3 |
100 |
85 |
Задача №1.2
По платежной матрице, составленной в задаче №1 определить: нижнюю и верхнюю цены игры, максиминную стратеги игрока А и минимаксную стратегию игрока В.
Задача №1.3
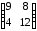
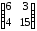
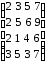
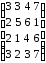
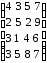
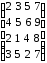
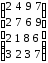
При помощи аналитического метода найти решение игры, заданной платежной матрицей. Данные брать в таблице 1.2
Таблица 1.2
|
Вариант |
Матрица |
Вариант |
Матрица |
|
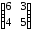
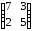
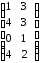
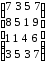
1 |
|
6 |
|
|
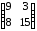
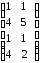
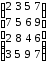
2 |
|
7 |
|
|
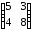
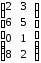
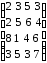
3 |
|
8 |
|
|
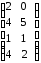
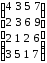
4 |
|
9 |
|
|
5 |
|
10 |
|
Задача №1.4
При помощи графического метода найти решение игры, заданной платежной матрицей. Данные брать в таблице 1.3
Таблица 1.3
|
1 |
|
6 |
|
|
2 |
|
7 |
|
|
3 |
|
8 |
|
|
4 |
|
9 |
|
|
5 |
|
10 |
|
Задача №1.5
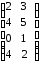
При помощи графического метода найти решение игры, заданной платежной матрицей. Данные брать в таблице 1.4
Таблица 1.4
|
1 |
|
6 |
|
|
2 |
|
7 |
|
|
3 |
|
8 |
|
|
4 |
|
9 |
|
|
5 |
|
10 |
|
Контрольная работа №2
Задача 2.1
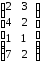
Дана
матрица последствий Q
. Составить матрицу рисков. Написать
рекомендации по принятию решений по
правилу Вальда, правилу Сэвиджа и правилу
Гурвица (при заданном
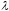 .
Данные брать в таблице 2.1
.
Данные брать в таблице 2.1
Таблица 2.1
|
Вариант |
Q |
|
Вариант |
Q |
|
|
1. |
|
0,3 |
6. |
|
0,5 |
|
2. |
|
0,1 |
7. |
|
0,6 |
|
3. |
|
0,4 |
8. |
|
0,8 |
|
4. |
|
0,15 |
9. |
|
0,21 |
|
5. |
|
0,14 |
10. |
|
0,35 |
Задача 2.2
В
условиях задачи 2.1 заданы вероятности
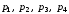 составить рекомендации по принятию
решений по правилу максимизации среднего
ожидаемого дохода и по правилу минимизации
среднего ожидаемого риска. Данные брать
в таблице 2.2
составить рекомендации по принятию
решений по правилу максимизации среднего
ожидаемого дохода и по правилу минимизации
среднего ожидаемого риска. Данные брать
в таблице 2.2
Таблица 2.2
|
Вариант |
|
|
|
|
Вариант |
|
|
|
|
|
1. |
0,20 |
0,30 |
0,10 |
0,40 |
6. |
0,35 |
0,35 |
0,15 |
0,15 |
|
2. |
0,40 |
0,10 |
0,10 |
0,40 |
7. |
0,15 |
0,45 |
0,25 |
0,15 |
|
3. |
0,30 |
0,50 |
0,10 |
0,10 |
8. |
0,25 |
0,25 |
0,35 |
0,15 |
|
4. |
0,20 |
0,60 |
0,10 |
0,10 |
9. |
0,15 |
0,25 |
0,30 |
0,30 |
|
5. |
0,70 |
0,15 |
0,11 |
0,04 |
10. |
0,30 |
0,25 |
0,10 |
0,35 |
Задача 2.3
Играют
двое
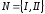 .
Игроки одновременно применяют стратегии
из множества
.
Игроки одновременно применяют стратегии
из множества
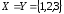 .
Природа реагирует на эти решения
стратегией
.
Природа реагирует на эти решения
стратегией
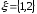 с вероятностями
с вероятностями
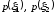 .
Выигрывает тот игрок который окажется
ближе к случайному числу
.
Выигрывает тот игрок который окажется
ближе к случайному числу
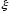 .
Составить матрицу выигрышей игроков.
Данные брать в таблице 2.3
.
Составить матрицу выигрышей игроков.
Данные брать в таблице 2.3
Таблица 2.3
|
Вариант |
|
|
Вариант |
|
|
|
1. |
0,20 |
0,80 |
6. |
0,35 |
0,65 |
|
2. |
0,30 |
0,70 |
7. |
0,45 |
0,55 |
|
3. |
0,40 |
0,60 |
8. |
0,95 |
0,05 |
|
4. |
0,60 |
0,40 |
9. |
0,25 |
0,75 |
|
5. |
0,15 |
0,85 |
10. |
0,65 |
0,35 |