Programmaот_1kurs_docx

Программа по линейной алгебре 1 курс 1 семестр

Векторы и действия над ними

Понятие вектора, его проекции и координаты.:вектором называют направленный отрезок.в фиксированной системе координат каждый вектор А однозначно определен своими коордтнатами А=(а1,а2,а3) вектор характеризцется числовой величиной и направлением. Проекция вектора на ось – это вектор, началом и концом которого являются соответственно проекции начала и конца заданного вектора.

Длина вектора. Длиной (модулем) вектора называется неотрицательное число, равное расстоянию между его началом и концом, то есть длина вектора - это длина отрезка . Длина обозначается/АВ/.Длина нулевого вектора0 равна нулю. Длина единичного вектора равна единице.

формула для нахождения длины вектора по его координатам на плоскости имеет вид . если на плоскости заданы точки и , то вектор имеет координаты и его длина вычисляется по формуле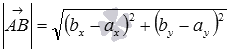

Ноль-вектор.вектор 0=(0,0,0)Направление ноль-вектора не имеет смысла,

Единичный вектор и его координаты. Е по ит-единичные вектор-все компоненты равны нулю,кроме одного на месте i.

Операции над векторами и их свойства (сложение векторов и умножение вектора на число). 1)сложение вектора а+в=с

2)разность направлена в сторону меньшего а-с=d

3)умножение вектора на число его направление то же,длина увеличивается в «с»раз.

Св-ва:1) Свойство коммутативности а+в=в+а

2)с(а+в)=са+св

3) Для любого ненулевого вектора а существует противоположный вектор и верно равенство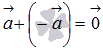

Понятие линейной комбинации векторов и ее свойства.(тут вставить буковки из лекции) Выражение вида____________________где_____________вектора,_______________некоторые действительные числаназывается линейной комбинацией векторов.

Система векторов(а1.А2,А3.)называется линейно независимой,если существует множество чисел________из которых хотя бы одно отлично от нуля.___.

__________________________________________________говорят,что вектор в представлен в виде линейной комбинации других векторов.

Система векторов линейно независима,если соотношение а1 выполняется только при нулевых альфа.

Понятие базиса векторов и координат вектора в базисе.совокупность линейно независимых векторов образует базис.виды базисов:афинный(вектора произвольны),ортогональный(вектора перпендикулярны),ортонормированный(перпендикульрны и длина каждого равна1)

Системы координат это совокупность точки и базиса(произвольная,декартова)

Коэффициенты называются координатами вектора с в базисе

Разложение вектора по базису.

Это в тетрадке прям теорема с доказательством теорема!!!!!!

Линейная зависимость и независимость векторов; связь между ними и свойства.

(тут тоже самое что и в понятии линейных комбинаций векторов и его св-ва)

Понятие ортонормированного базиса.

Система векторов А1,А2.а3……Аn называется ортонормированной если она ортогональна и длина каждого вектора системы равна единице

Понятие n-мерного Евклидова пространства.

совокупность всех n-мерных векторов,рассматривая с определенными в ней операциями сложения векторов и умножения вектора на число,называется n-мерным координатным пространством. мерное евклидово пространство обозначается также часто используется обозначение

Норма вектора в Евклидовом пространстве. длина вектора является нормой на евклидовом векторном пространстве, а функция задаёт на евклидовом пространстве структуру метрического пространства (эта функция называется евклидовой метрикой). В частности, расстояние между элементами (точками)х и у и координатного пространства задаётся формулой

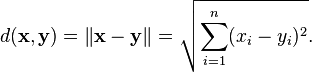
Понятие системы координат.это не нашла!!!!!!

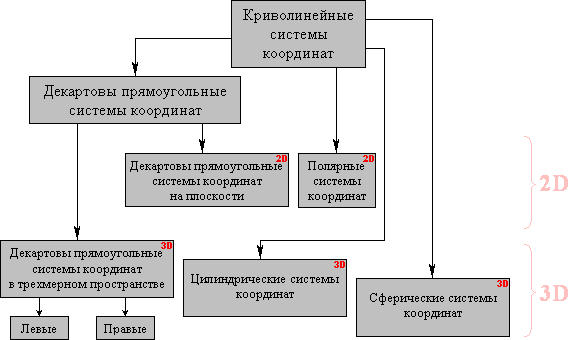
Виды систем координат. Положение любой точки P в пространстве (в частности, на плоскости) может быть определено при помощи той или иной системы координат. Числа, определяющие положение точки, называются координатами этой точки.

координатные системы - декартовы прямоугольные точки P на плоскости называются взятые с определенным знаком расстояния (выраженные в единицах масштаба) этой точки до двух взаимно перпендикулярных прямых - осей координат или, что то же, проекции радиус-вектора r точки P на две взаимно перпендикулярные координатные оси

Кроме прямоугольных систем координат существуют косоугольные системы.Прямоугольные и косоугольные координатные системы объединяются под названием декартовых систем координат.

на плоскости применяют полярные системы координат, а в пространстве - цилиндрические или сферические системы координат. Обобщением всех перечисленных систем координат являются криволинейные системы

Ориентирование тройки векторов. Упорядоченная тройка некомпланарных векторов называется правой, если, глядя с конца третьего вектора на плоскость первых двух, мы видим поворот от первого вектора ко второму пократчайшему пути происходящим против часовой стрелки. В противном случае тройка называется левой. ------------это левая

Свойства ориентированной тройки векторов.

1. { – правая}следовательно { – левая}.

2. { – правая}следовательно { – левая}.

3. { – правая}следовательно { – правая}.

Понятие радиус-вектора. Ра́диус-ве́ктор (обычно обозначается r — вектор, задающий положения точки в пространстве (например, гильбертовом или векторном) относительно некоторой заранее фиксированной точки , называемой началом координат.

Для произвольной точки в пространстве, радиус-вектор — это вектор, идущий из начала координат в эту точку.

Длина радиус-вектора, или его модуль, определяет расстояние, на котором точка находиnся от начала координат, а стрелка указывает направление на эту точку пространства.

На плоскости углом радиус-вектора называется угол, на который радиус-вектор повёрнут относительно оси абсцисс в направлении против часовой стрелки.

Выражение координат произвольного вектора через компоненты радиус-векторов.

!!!!!!!!!!!!!!!не нашла

Направляющие косинусы вектора и их свойства. Направляющие косинусы вектора a – это косинусы углов, которые вектор образует с положительными полуосями координат. Чтобы найти направляющие косинусы вектора a необходимо соответствующие координаты вектора поделить на модуль вектора._св-во: cos2 α + cos2 β = 1

Длина отрезка. Рассчитаем длину отрезка А, для этого найдем квадратный корень:

A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²).

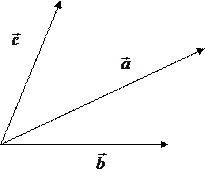
Скалярное произведение векторов и его свойства. Геометрическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:

a · b = |a| · |b| cos α

Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.

Св-ва:1) Операция скалярного умножения коммуникативна:

a · b = b · a

2) Операция скалярного умножения дистрибутивна:

(a + b) · c = a · c + b · c

3) Скалярное произведение вектора самого на себя равно квадрату его модуля:

a · a = |a|2

4) Если скалярное произведение двух не нулевых векторов равно нулю, то эти вектора ортогональны:

a ≠ 0, b ≠ 0, a · b = 0 <=> a ┴ b

Выражение скалярного произведения векторов через их координаты. Пусть заданы два вектора скалярно умножим: 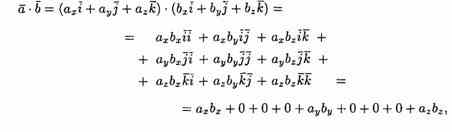т.е. Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.

Угол между векторами. Определение угла φ между ненулевыми векторами а = (ax; ay; az) и b=( bх; bу; bz):

Отсюда следует условие перпендикулярности ненулевых векторов а и b

Деление отрезка в заданном отношении. Это в тетради расписано как задача!!!!!!!

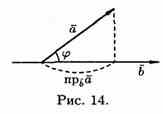
Геометрический смысл скалярного произведения векторов.

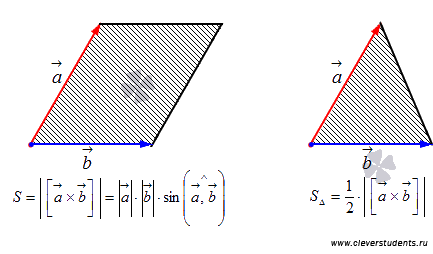
Векторное произведение векторов и его свойства. Векторным произведением вектора а на вектор b называется вектор с, который:

1. Перпендикулярен векторам a и b, т. е. с^а и с^b;

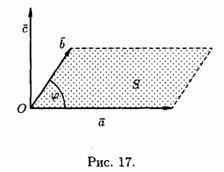
2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах (см. рис. 17), т. е.

3.Векторы a, b и с образуют правую тройку.

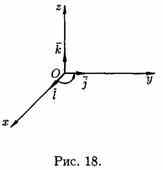
4/ его длина равна произведению длин векторов и на синус угла между ними

Св-ва: антикоммутативность

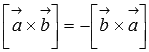
свойство дистрибутивности

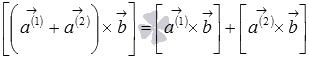
сочетательное свойство 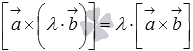или

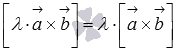
Выражение вектора векторного произведения векторов через координаты. В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов и есть вектор 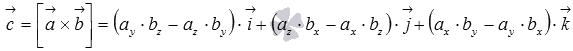, где - координатные векторы.

Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты , во второй строке находятся координаты вектора а в третьей – координаты вектора в заданной прямоугольной системе координат: 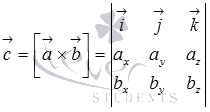если разложить,то получим_

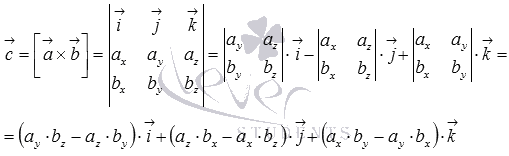
Геометрический смысл модуля векторного произведения векторов. длина векторного произведения векторов и равна площади параллелограмма со сторонами и и углом между ними, равным .

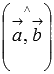Смешанное произведение векторов и его свойства. Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторноскалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.

Св-ва: 1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. (а х b )•с=(b х с)•а=(с х а)•b .2) Смешанное произведение не меняется при перемене местами знаков вкторного и скалярного умножения, т. е. (ахb )•с=а*(bx с).3) Смешанное произведение ненулевых векторов а, b и с равно нулю огда и только тогда, когда они компланарны

Геометрическое истолкование смешанного произведения векторов. геометрический смысл выражения (ахb )*с. Построим параллелепипед, ребрами которого являются векторы а, b , с и вектор d =ахb 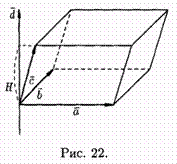смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.