Задача № 4

В результате маркетингового исследования установлено, что функции спроса и предложения имеют вид:

1.- спроса,

- предложения,

где p– цена товара.

Найти:

1. Равновесную цену p₀.

2. Эластичность спроса и предложения для этой цены.

3. Изменение дохода при увеличении цены на 5%от равновесной.

Решение

1)Определяем равновесную ценуp₀, при которой спрос равен предложению.

Отсюда p₀=2. (Отрицательный корень отбрасываем, как не имеющий экономического смысла).

График зависимостей спроса и предложения от цены представлен на рис. 1.

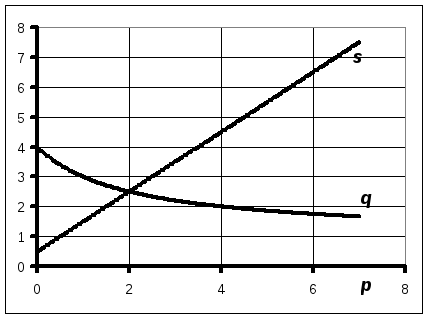
Рис.1. Зависимости спроса и предложения от цены.

2)Находим эластичности спроса и предложения для равновесной цены.

2.1.Находим производныеq’(p)иs’(p).

2.2.Получаем общие выражения для эластичностей спроса и предложения.

2.3.Вычисляем эластичности спроса и предложения при равновесной цене.

Таким образом, при увеличении цены на 1% от равновесного значения спрос уменьшается (т.к. «-») на 0, 3%, а предложение возрастает (т.к. «+») на 0,8%.

3)Выведем общее выражение для эластичности доходаR=pqпо цене, пользуясь свойствами эластичности и подставим в него численные значенияp₀ иE₂(q):

Это означает, что при увеличении цены на 1%от равновесного значения доход увеличивается на0,7%.Следовательно, при увеличении цены на5%от ее равновесного значения доход увеличится на50,7%=3,5%.

Ответ: 1) равновесная цена товара равна2; 2) при увеличении цены на 1% от равновесного значения спрос уменьшается на 0, 3%, а предложение возрастает на 0,8%; 3) при увеличении цены на 5% от ее равновесного значения доход увеличится на 3,5%.

Задача № 5

Фирма реализует произведенную продукцию по цене p, а зависимость издержекCимеет вид , гдеq- объём производства.

Используя методы дифференциального исчисления:

1. выполнить полное исследование функции зависимости прибыли фирмы Пот объема производстваqпостроить ее график.

2. Найти оптимальный для фирмы объем выпуска продукции и соответствующую ему прибыль.

a=7; b=0,01; c=5; p=10

Решение

Учитывая, что прибыль представляет собой разность между доходом и издержками, и подставляя численные данные, получаем явный вид зависимости прибыли от объема производства:

1)Выполняем полное исследование функцииП(q)

1.1.Область определенияD(П)=[0;+∞].

1.2.Находим первую и вторую производнуюП’(q) и П’’(q)

1.3.Находим критические точки, решая уравнениеП^’(q)=0

1.4.Наносим критическую точку на числовую ось, и находим знак первой производной на каждом из получившихся интервалов:

Из рисунка делаем выводы о том, что функция возрастает при , а убывает при ; в точкеq=10функция имеет максимум.

Вычислим значение функции в этой точке:

1.5.Найдем точку перегиба графика функции, решая уравнениеП’’(q)=0

Так как случай q=0 не представляет практического интереса, будем считать, что график функции точек перегиба не имеет.

1.6.Найдем, на каких интервалах график функции выпуклый, а на каких—вогнутый.

Так как на всей области определения, делаем вывод о том, что график функции выпуклый на всей области определения.

1.7.Сводим все полученные результаты в итоговую таблицу:

Таблица 1.

q	П’(q)	П’’(q)	П(q)	Примечания
0	+	—	-5	график выпуклый
(0;10)	+	—	↑	график выпуклый
10	0	—	15	максимум
(10;+∞)	—	—	↓	график выпуклый

1.8.Строим схематический график функции

Рис.2. График зависимости прибыли от объема выпуска продукции.

2)Очевидно, что оптимальным для фирмы является объем выпуска, равный 10, при этом прибыль будет максимальна и составит 15.

Ответ в данной задаче нет необходимости выписывать отдельно, так как он фактически содержится в таблице 1.