
- •Глава 8. Исследование поведения функций
- •§ 8.1. Исследование поведения функций одной переменной
- •8.1.1. Условия монотонности функции
- •8.1.2. Локальные экстремумы функции
- •8.1.3. Наибольшее и наименьшее значение функции на отрезке
- •8.1.4. Выпуклость функции
- •8.1.5. Асимптоты графика функции
- •§ 8.2. Экстремумы функций нескольких переменных
- •8.2.1. Необходимое условие экстремума
- •8.2.2. Достаточное условие экстремума функции
- •§ 8.3. Глобальные экстремумы функции
- •8.3.1. Понятие глобального экстремума функции
- •8.3.2. Необходимое условие глобального экстремума
- •8.3.3. Метод Лагранжа отыскания
8.3.2. Необходимое условие глобального экстремума
Лемма. Система
уравнений
![]() ,
,![]() ,имеет
решения при любых значениях
,имеет
решения при любых значениях
![]() ,
если векторы
,
если векторы![]() линейно независимы.
линейно независимы.
Доказательство леммы приводится в приложении 3. ■
Следствие.
Если система векторов
![]() линейно независима, то найдется такой
вектор
линейно независима, то найдется такой
вектор![]()
![]() ,
что
,
что
![]() (
(![]() ).
(1)
).
(1)
Доказательство. Из леммы следует, что система уравнений
![]() (
(![]() )
)
имеет решение
![]()
![]() ,
которое удовлетворяет условию (1). ■
,
которое удовлетворяет условию (1). ■
Теорема 8.10
(необходимое
условие глобального экстремума функции).
Функция
![]() определена на множестве
определена на множестве
![]() ,
,
![]() .
.
Функции
![]() и
и![]() при любом
при любом![]() дифференцируемы
в точке глобального экстремума
дифференцируемы
в точке глобального экстремума
![]() функции
функции![]() ,.
Тогда система векторов
,.
Тогда система векторов
![]() ,
,
![]() ;
;![]()
![]() ,
,
где
![]() ,
линейно зависима.
,
линейно зависима.
Доказательство от противного, т.е. пусть система векторов
![]() ,
,
![]() ;
;![]()
![]()
линейно независима.
Из следствия к лемме следует, что найдется
такой вектор
![]()
![]() ,
что
,
что
![]() ,
,
![]() ,
,
![]() (
(![]() ,
,![]() ,
,![]() ).
).
Так как
![]() мерный
вектор
мерный
вектор![]()
![]() удовлетворяет условию
удовлетворяет условию
![]()
![]() ,
,
то из свойства
градиента следует, что можно построить
такое число
![]() ,
что при всех
,
что при всех![]()
![]()
![]() .
(2)
.
(2)
Так как
![]() мерный
вектор
мерный
вектор![]()
![]() удовлетворяет условию
удовлетворяет условию
![]() ,
,
![]() ,
(
,
(![]() ,
,![]() ),
),
то можно построить
такое число
![]() (теорема
6.9), что при всех
(теорема
6.9), что при всех![]() точка
точка
![]() (3)
(3)
Обозначим
символом
![]() .
Тогда при всех
.
Тогда при всех![]() условия (2) и (3) справедливы, что противоречит
определению глобального экстремума. ■
условия (2) и (3) справедливы, что противоречит
определению глобального экстремума. ■
8.3.3. Метод Лагранжа отыскания
глобальных экстремумов
В этом пункте
будет изложен метод Лагранжа для
отыскания глобальных экстремумов
функции
![]() на множестве
на множестве
![]() ,
,
где
![]() непрерывны на всем пространстве
непрерывны на всем пространстве![]() ,
функции
,
функции![]() и
и![]() при
при
любом
![]() дифференцируемы на множестве
дифференцируемы на множестве![]() ,
,![]() .
.
Метод множителей Лагранжа состоит в том, что вводится вспомогательная функция
![]() ,
,
которая называется
функцией Лагранжа, а неизвестные
![]() —
множители Лагранжа. Отыскание глобального
экстремума функции
—
множители Лагранжа. Отыскание глобального
экстремума функции![]() сводится к нахождению критических точек
функции Лагранжа.
сводится к нахождению критических точек
функции Лагранжа.
Теорема 8.10.
Если
![]() —
глобальный
экстремум функции
—
глобальный
экстремум функции
![]() на множестве
на множестве
![]() ,то найдется
такой ненулевой набор чисел
,то найдется
такой ненулевой набор чисел
![]() ,
что точка
,
что точка
![]() является
решением
системы уравнений
является
решением
системы уравнений
 (4)
(4)
Доказательство. Из теоремы 8.10 следует, что система векторов
![]() ,
,
![]() ,…,
,…,![]() ,
,
![]() ,
,
![]() ,
(5)
,
(5)
линейно зависима,
где
![]() .
Следовательно, найдется такой ненулевой
набор чисел
.
Следовательно, найдется такой ненулевой
набор чисел![]() ,
что равенство
,
что равенство
![]() (6)
(6)
является истиной.
Полагая
![]() при всех
при всех![]() ,
разложение (6) перепишем в виде
,
разложение (6) перепишем в виде
![]()
![]() (7)
(7)
Из равенства (7)
следует, что
![]() -я
координата вектора, находящегося в
левой части равенства (7) равна нулю при
любом
-я
координата вектора, находящегося в
левой части равенства (7) равна нулю при
любом![]() .
Так как
.
Так как![]() -я
координата линейной комбинации векторов
равна сумме их
-я
координата линейной комбинации векторов
равна сумме их![]() -х
координат, то из равенства (7) имеем
-х
координат, то из равенства (7) имеем
![]()
![]() ,
,
![]() .
(8)
.
(8)
Левая часть
равенства (8) равна частной производной
функции Лагранжа по переменной
![]() в точке
в точке![]() ,
поэтому из равенства (7) следует
,
поэтому из равенства (7) следует
![]() ,
,
![]() .
(9)
.
(9)
Второе уравнение
системы (4) в точке
![]() имеет вид
имеет вид
![]()
![]()
![]() .
(10)
.
(10)
Последнее равенство
является истиной:
![]() ,
если
,
если![]() ,
если же
,
если же![]() ,
то
,
то![]() .
Итак, равенство (10) справедливо при любом
.
Итак, равенство (10) справедливо при любом![]() .
.
Из равенств (9) и
(10) следует, что точка
![]() является решением системы уравнений
(4) и числа
является решением системы уравнений
(4) и числа
![]() образуют ненулевой набор. ■
образуют ненулевой набор. ■
Замечание.
Теорема
8.10 справедлива также и тогда, когда
функция
![]() определена на множестве
определена на множестве
![]() .
.
В этом случае
функция Лагранжа
![]() имеет вид:
имеет вид:
![]() .
▲
.
▲
Из теоремы 8.10
вытекает следующий алгоритм отыскания
глобальных экстремумов функции
![]() на множестве
на множестве![]() .
.
1. Доказать, что
функция
![]() на множестве
на множестве![]() имеет глобальный экстремум.
имеет глобальный экстремум.
2. Преобразовать
неравенства, задающие множества
![]() к виду
к виду![]() .
.
3. Построить функцию Лагранжа и систему уравнений (4).
4. Найти все
решения системы уравнений (4), у которых
значения неизвестных
![]() не все равны нулю.
не все равны нулю.
5. Решения, системы
(4), найденные в пункте 4, укоротить,
отбросив значения неизвестных
![]() ,
и выбрать среди них те, которые принадлежат
множеству
,
и выбрать среди них те, которые принадлежат
множеству![]() .
.
6. Вычислить
значения функции
![]() на решениях, отобранных в пункте 5.
Решения, на которых
на решениях, отобранных в пункте 5.
Решения, на которых![]() принимает наибольшее и наименьшее
значения являются точками глобального
экстремума функции
принимает наибольшее и наименьшее
значения являются точками глобального
экстремума функции![]() .
.
Примеры. Найти
глобальные экстремумы функции
![]() на множестве
на множестве![]() .
.
1.
![]() ,
,
![]() .
.
Решение. Так
как множество
![]() замкнуто (теорема 4.9) и ограничено:
замкнуто (теорема 4.9) и ограничено:![]() ,
,![]() ,
то функция
,
то функция![]() имеет глобальные экстремумы на множестве
имеет глобальные экстремумы на множестве![]() .
Функция Лагранжа имеет вид
.
Функция Лагранжа имеет вид
![]() .
.
Напишем систему
уравнений, решением которой являются
глобальные экстремумы функции
![]() :
:
 (11)
(11)
Если
![]() ,
то из первого уравнения системы (11), что
,
то из первого уравнения системы (11), что![]() .
Следовательно, при
.
Следовательно, при![]() система уравнений (11) не имеет решений,
у которых значения неизвестных
система уравнений (11) не имеет решений,
у которых значения неизвестных![]() не равны нулю одновременно.
не равны нулю одновременно.
Если же
![]() ,
то систему (11) можно переписать в виде
,
то систему (11) можно переписать в виде

![]()

![]()
 (12)
(12)
Система уравнений (12) имеет два решения
![]() ,
,
![]() ,
,
![]() .
.
Укороченная система
решений имеет вид:
![]() ,
,
![]() .
Эти точки принадлежат множеству
.
Эти точки принадлежат множеству![]() .
.
Так
![]() ,
,![]() ,
то
,
то![]()
![]() — точка глобального минимума (максимума)
и
— точка глобального минимума (максимума)
и![]() ,
,![]() .
.
2.
![]() ,
,
![]() .
.
Решение.
Множество
![]() замкнуто (теорема 4.9) и ограничено:
замкнуто (теорема 4.9) и ограничено:![]() ,
,![]() ,
,
![]() .
Следовательно, функция
.
Следовательно, функция
![]() имеет глобальные экстремумы на множестве
имеет глобальные экстремумы на множестве![]() .
Функция Лагранжа имеет вид
.
Функция Лагранжа имеет вид
![]() .
.
Напишем систему
уравнений, решением которой являются
глобальные экстремумы функции
![]() :
:
 (13)
(13)
Если
![]() ,
то системa
уравнений (13) имеет вид
,
то системa
уравнений (13) имеет вид
![]() ,
,
![]() ,
,![]() ,
,
![]() .
(14)
.
(14)
Так как набор
неизвестных
![]() ,
,![]() должен быть ненулевым, то
должен быть ненулевым, то![]() .
Значит, произвольное решение системы
(14) имеет вид:
.
Значит, произвольное решение системы
(14) имеет вид:
![]() .
Укороченное решение
.
Укороченное решение
![]() не принадлежит множеству
не принадлежит множеству![]() .
.
Если же
![]() ,
то введем новую переменную
,
то введем новую переменную![]() и перепишем систему уравнений (13) в виде
и перепишем систему уравнений (13) в виде
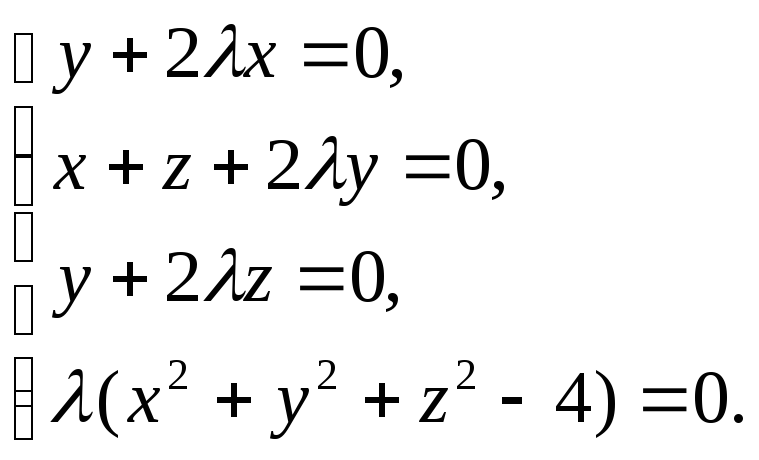 (15)
(15)
Если в системе
уравнений (15) неизвестное
![]() ,
т.е.
,
т.е.![]() ,
то система примет вид
,
то система примет вид
![]() ,
,
![]() ,
,
![]() ,
,![]() .
(16)
.
(16)
Произвольное
решение системы (16) имеет вид:
![]() .
Укороченная точка
.
Укороченная точка
![]() будет принадлежать множеству
будет принадлежать множеству![]() ,
если
,
если![]() ,
т.е. если
,
т.е. если![]() .
Итак, при
.
Итак, при![]() получили решения
получили решения
![]() и
и
![]() системы (15), укороченные точки которых
системы (15), укороченные точки которых
![]() ,
,
![]()
принадлежат
множеству
![]() .
.
В случае
![]() преобразуем систему уравнений (16),
заменив первое уравнение разностью
первого и третьего уравнений,
преобразуем систему уравнений (16),
заменив первое уравнение разностью
первого и третьего уравнений,

![]()

![]()
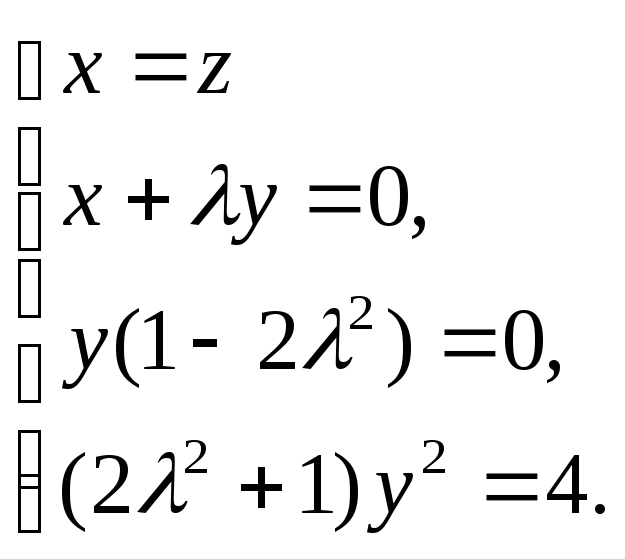 (17)
(17)
Система уравнений
(17) имеет четыре типа решений
![]()
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Укороченные точки
![]() ,
,![]() ,
,![]() ,
,![]()
принадлежат
множеству
![]() .
.
Найдем значения
функции
![]() на точках
на точках![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() и
и![]() :
:
![]() ,
,
![]() ,
,![]() .
.
Итак, точки
![]() и
и![]() — точки глобального минимума функции,
а точки
— точки глобального минимума функции,
а точки![]() и
и![]() — точки глобального максимума функции.
Значение глобальных экстремумов функции
равны:
— точки глобального максимума функции.
Значение глобальных экстремумов функции
равны:![]() ,
,![]() .
●
.
●
Задачи
Найти точки
глобального экстремума функции
![]() на множестве
на множестве![]() .
.
1.
![]() ,
,![]() .
.
2.
![]() ,
,![]() .
.
3.
![]() ,
,![]() .
.
4.
![]() ,
,![]() .
.
5.
![]() ,
,![]() .
.
6.
![]() ,
,![]() .
.
7.
![]() ,
,![]() .
.
Ответы
1.
![]() ,
,![]() .
.
2.
![]() ,
,![]() .
.
3.
![]() ,
,![]() .
.
4.
![]() ,
,![]() .
.
5.
![]() ,
,![]() .
.
6.
![]() ,
,![]() .
.
7.
![]() ,
,![]() .
.
