
- •Тема 8. Модели динамического программирования
- •1. Предмет динамического программирования
- •2. Постановка задачи динамического программирования
- •3. Принцип оптимальности и математическое описание динамического процесса управления
- •4. Оптимальное распределение инвестиций
- •I этап. Условная оптимизация.
- •II этап. Безусловная оптимизация.
- •5. Выбор оптимальной стратегии обновления оборудования (задача о замене оборудования)
- •I этап. Условная оптимизация.
- •2 Этап. Безусловная оптимизация.
- •6. Выбор оптимального маршрута перевозки грузов
- •II этап. Безусловная оптимизация.
- •7. Построение оптимальной последовательности операций в коммерческой деятельности
- •1 Этап. Условная оптимизация.
- •2 Этап. Безусловная оптимизация.
- •Индивидуальные задания
- •Контрольные вопросы
2. Постановка задачи динамического программирования
Общая
постановка задачи динамического
программирования формулируется следующим
образом. Имеется некоторая управляемая
система
![]() ,
характеризующаяся определенным набором
параметров. В этой системе происходят
какие-то процессы (экономические,
производственные, технологические и
т.п.), которые можно представить как
многошаговые. На каждом шаге процессам
в системе соответствуют определенные
значения параметров, описывающихсостояние
системы.
Заданы условия, позволяющие определять
или начальное, или конечное состояние
системы, или оба этих состояния. Иногда
задаются области начальных и конечных
состояний. Поскольку управление системой
осуществляется для достижения конкретной
цели, то указан показатель эффективности
управления, называемый целевой функцией,
численно выражающий эффект («выигрыш»),
получаемый при тот или ином управлении
из множества допустимых управлений.
,
характеризующаяся определенным набором
параметров. В этой системе происходят
какие-то процессы (экономические,
производственные, технологические и
т.п.), которые можно представить как
многошаговые. На каждом шаге процессам
в системе соответствуют определенные
значения параметров, описывающихсостояние
системы.
Заданы условия, позволяющие определять
или начальное, или конечное состояние
системы, или оба этих состояния. Иногда
задаются области начальных и конечных
состояний. Поскольку управление системой
осуществляется для достижения конкретной
цели, то указан показатель эффективности
управления, называемый целевой функцией,
численно выражающий эффект («выигрыш»),
получаемый при тот или ином управлении
из множества допустимых управлений.
В экономических системах целевая функция может определять прибыль, затраты, рентабельность, объем производства и т.п.
Задача динамического программирования (ДП) состоит в выборе из множества допустимых управлений такого, которое переводит систему из начального состояния в конечное, обеспечивая при этом целевой функции экстремум (минимум или максимум в зависимости от ее экономической сути). Такое управление называется оптимальным.
П остановку
задачи динамического программирования
рассмотрим на примере инвестирования,
связанного с распределением средств
между предприятиями. В результате
управления инвестициями система
последовательно переводится из начального
состояния
остановку
задачи динамического программирования
рассмотрим на примере инвестирования,
связанного с распределением средств
между предприятиями. В результате
управления инвестициями система
последовательно переводится из начального
состояния![]() в конечное
в конечное
![]() .
Предположим, что управление можно
разбить наn
шагов и решение принимается последовательно
на каждом шаге, а управление представляет
собой совокупность n
пошаговых управлений. На каждом шаге
необходимо определить два типа переменных
- переменную состояния системы
.
Предположим, что управление можно
разбить наn
шагов и решение принимается последовательно
на каждом шаге, а управление представляет
собой совокупность n
пошаговых управлений. На каждом шаге
необходимо определить два типа переменных
- переменную состояния системы
![]() и переменную управления
и переменную управления![]() .
Переменная
.
Переменная![]() определяет, в каких состояниях может
оказаться система на рассматриваемомk-м
шаге. В зависимости от состояния S
на этом шаге можно применить некоторые
управления, которые характеризуются
переменной
определяет, в каких состояниях может
оказаться система на рассматриваемомk-м
шаге. В зависимости от состояния S
на этом шаге можно применить некоторые
управления, которые характеризуются
переменной
![]() ,
которые удовлетворяют определенным
ограничениям и называются допустимыми.
,
которые удовлетворяют определенным
ограничениям и называются допустимыми.
Допустим,
![]() – управление, переводящее систему из
состояния
– управление, переводящее систему из
состояния![]() в состояние
в состояние
![]() ,
а
,
а![]() - есть
состояние системы на k-м
шаге управления. Тогда последовательность
состояний системы можно представить в
виде графа, представленного на рис. 1.
- есть
состояние системы на k-м
шаге управления. Тогда последовательность
состояний системы можно представить в
виде графа, представленного на рис. 1.

Рис. 1. График состояний системы.
П рименение
управляющего воздействия
рименение
управляющего воздействия![]() ,
на каждом шаге переводит систему в новое
состояние S1
(S,
,
на каждом шаге переводит систему в новое
состояние S1
(S,
![]() )
и приносит некоторый результат
)
и приносит некоторый результат ![]() (S,
(S,
![]() ).
Для каждого возможного состояния на
каждом шаге среди всех возможных
управлений выбирается оптимальное
управление
).
Для каждого возможного состояния на
каждом шаге среди всех возможных
управлений выбирается оптимальное
управление ![]() ,
такое, чтобы результат, который достигается
за шаги с k-го
по последний n-й,
оказался бы оптимальным.
,
такое, чтобы результат, который достигается
за шаги с k-го
по последний n-й,
оказался бы оптимальным.
Числовая
характеристика этого результата
называется функцией
Беллмана
![]() и зависит от номера шага k
и состояния системы S.
и зависит от номера шага k
и состояния системы S.
Задача
динамического программирования
формулируется следующим образом:
требуется определить такое управление
![]() ,
переводящее систему из начального
состояния в конечное состояние
,
переводящее систему из начального
состояния в конечное состояние![]() ,
при котором целевая функция принимает
наибольшее (наименьшее) значение
,
при котором целевая функция принимает
наибольшее (наименьшее) значение
![]() .
.
Особенности математической модели динамического программирования заключаются в следующем:
задача оптимизации формулируется как конечный многошаговый процесс управления;
целевая функция (выигрыш) является аддитивной и равна сумме целевых функций каждого шага:
![]()
выбор управления
 на каждом шаге зависит только от
состояния системы k
этому шагу
на каждом шаге зависит только от
состояния системы k
этому шагу
 и не влияет на предшествующие шаги (нет
обратной связи);
и не влияет на предшествующие шаги (нет
обратной связи);состояние системы
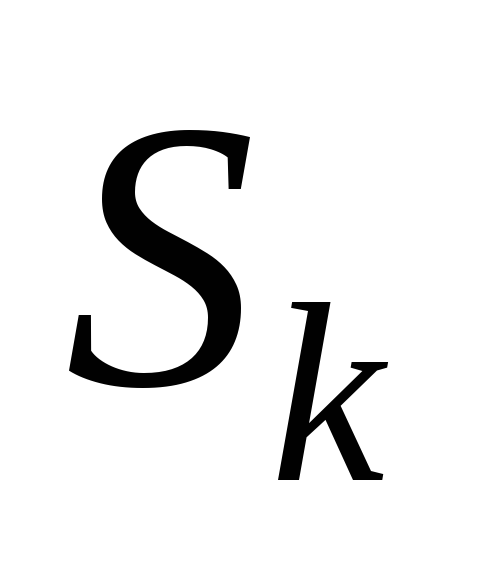 после каждого шага управления зависит
только от предшествующего состояния
системы и этого управляющего воздействия
после каждого шага управления зависит
только от предшествующего состояния
системы и этого управляющего воздействия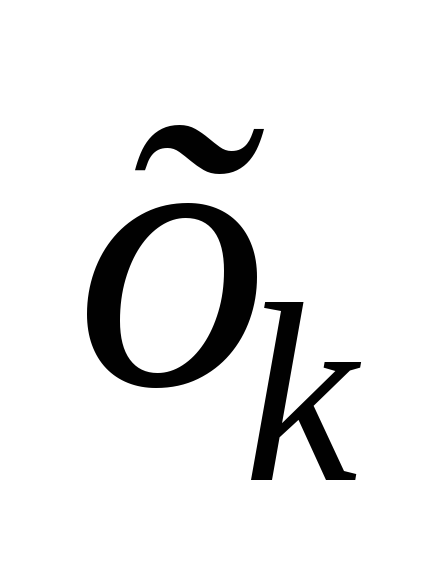 (отсутствие последействия) и может быть
записало в виде уравнения состояния:
(отсутствие последействия) и может быть
записало в виде уравнения состояния:

на каждом шаге управление
 зависит от конечного
числа управляющих переменных, а состояние
системы зависит — от конечного числа
параметров;
зависит от конечного
числа управляющих переменных, а состояние
системы зависит — от конечного числа
параметров; оптимальное управление представляет собой вектор
 ,
определяемый последовательностью
оптимальных пошаговых управлений:
,
определяемый последовательностью
оптимальных пошаговых управлений: ,
число которых и определяет количество
шагов задачи.
,
число которых и определяет количество
шагов задачи.
