
Задание 1
По данной производственной функции найти средние и предельные производительности каждого ресурса, частные эластичности выпуска по каждому ресурсу, эластичность производства и предельную технологическую норму замены.
![]()
Решение:
Средние производительности:
 ,
,
 .
.
Предельные производительности равны:
 ,
,
![]() .
.
Частные эластичности равны:
 ,
,
 .
.
Эластичность
производства:
 .
.
Технологическая норма замены есть:
 .
.
Задание 2
Некоторое предприятие затрачивает а1= 3 тыс. тонн ресурса иb1= 30 тыс. часов труда для выпуска с1= 68 тыс. единиц продукции. В результате расширения производства оказалось, что при затратах а2 = 3.5 тыс. тонн ресурса выпуск возрос до с2= 70 тыс. единиц продукции, а при увеличении трудоемкости доb2= 32 тыс. часов, выпуск возрос до с3=72тыс. единиц продукции. Найти линейную производственную функцию и производственную функцию Кобба-Дугласа.
Решение:
Запишем для удобства исходные данные в виде таблицы:
|
x1 |
3 |
3.5 |
– |
|
x2 |
30 |
– |
32 |
|
y |
68 |
70 |
72 |
Линейная
функция
![]() .
.
Найдем параметры функции:
 ,
,
 .
.
Получаем
![]() .
.
Для нахождения bиспользуем первый столбец таблицы:
![]() ,
откуда
,
откуда
![]() .
.
В результате линейная производственная функция имеет вид:
![]() .
.
Производственная функция Кобба-Дугласа имеет вид:
![]() .
.
Коэффициенты уравнения:
 ,
,
 .
.
Получаем
![]() .
.
Для нахождения bиспользуем первый столбец таблицы:
![]() ,
откуда
,
откуда
![]() .
.
В результате производственная функция Кобба-Дугласа имеет вид:
![]() .
.
Задание 3
Целевая
функция потребления имеет вид
![]() .
Цена на первое благо равна
.
Цена на первое благо равна
![]() ,
а на второе благо
,
а на второе благо![]() .
Доход составляет D = 450. Найти:
.
Доход составляет D = 450. Найти:
а)
оптимальный набор благ
![]() ;
;
б)
функцию спроса по цене на первое благо
![]() ;
;
в)
функцию спроса по доходу на первое благо
![]() ;
;
Решение:
1) Находим оптимальный набор благ. Задача оптимального программирования имеет вид:
![]()
 .
.
Для
ее решения выражаем из бюджетного
ограничения
![]() одну переменную через другую:
одну переменную через другую:![]() .
.
Подставляем
в целевую функцию:
![]() .
.
Находим производную и приравниваем ее к 0:
 или
или
![]() ,
откуда
,
откуда![]() .
.
Тогда
![]() .
.
Таким образом, оптимальный набор благ составляет 15 и 22.5 единиц.
2)
Находим теперь функцию спроса на
первое благо по цене на него. Для
этого в бюджетном ограничении вместо
фиксированного значения вводим цену
первого блага
![]() :
:![]() ,
откуда
,
откуда![]() .
Подставляем в целевую функцию:
.
Подставляем в целевую функцию:
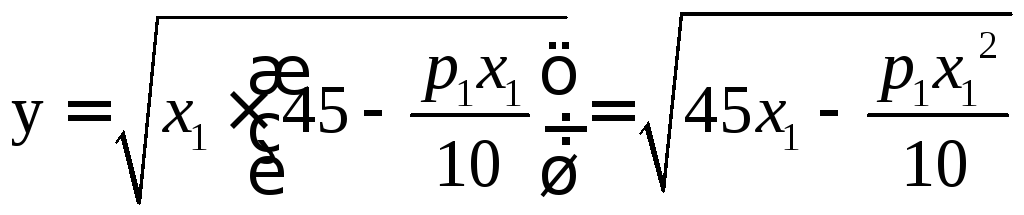 .
.
Находим производную и приравниваем ее к 0:
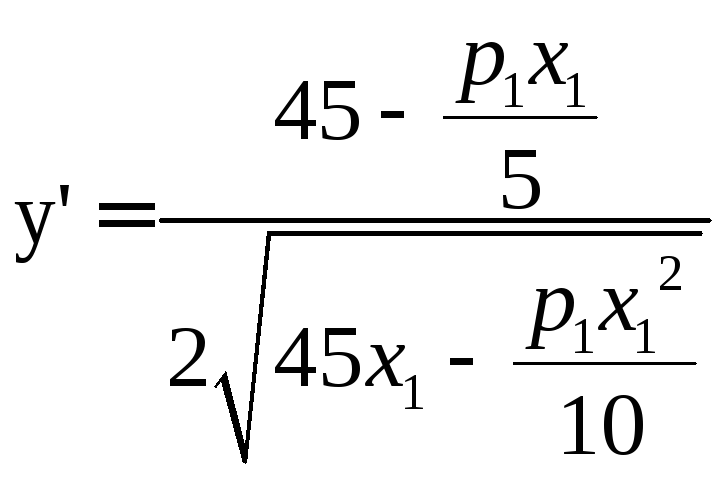 или
или
![]() ,
откуда
,
откуда – функция спроса на первое благо по
цене.
– функция спроса на первое благо по
цене.
3)
Находим теперь функцию спроса на первое
благо по доходу. Для этого выражаем из
бюджетного ограничения
![]() одну переменную через другую:
одну переменную через другую:![]() .
.
Подставляем в целевую функцию:
 .
.
Находим производную и приравниваем ее к 0:
 или
или
![]() ,
откуда
,
откуда![]() – функция спроса на первое благо по
доходу.
– функция спроса на первое благо по
доходу.
Задание 4
Межотраслевой баланс производства и распределения продукции для 4 отраслей имеет вид:
Найти конечный продукт каждой отрасли, чистую продукцию каждой отрасли, матрицу коэффициентов прямых затрат. Какой будет конечный продукт каждой отрасли, если валовой продукт первой отрасли увеличится в 2 раза, у второй увеличится на половину, у третьей не изменится, у четвертой – уменьшится на 10 процентов.
Матрица межотраслевых материальных связей xijи матрица валового выпуска Xjприведены в таблице:
|
Производящие отрасли |
Потребляющие отрасли |
Валовой продукт | |||
|
1 |
2 |
3 |
4 | ||
|
1 |
80 |
45 |
85 |
95 |
475 |
|
2 |
25 |
35 |
20 |
30 |
825 |
|
3 |
15 |
15 |
55 |
75 |
450 |
|
4 |
95 |
5 |
5 |
95 |
820 |
Решение:
1) Найдем чистую продукцию отраслей, используя формулу:
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
2) Конечный продукт отраслей:
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
3)
Элементы матрицы прямых затрат определяем
по правилу
![]() .
.
Например,
![]() ,
,![]() .
.
В
результате
 .
.
4)
Новый валовой продукт
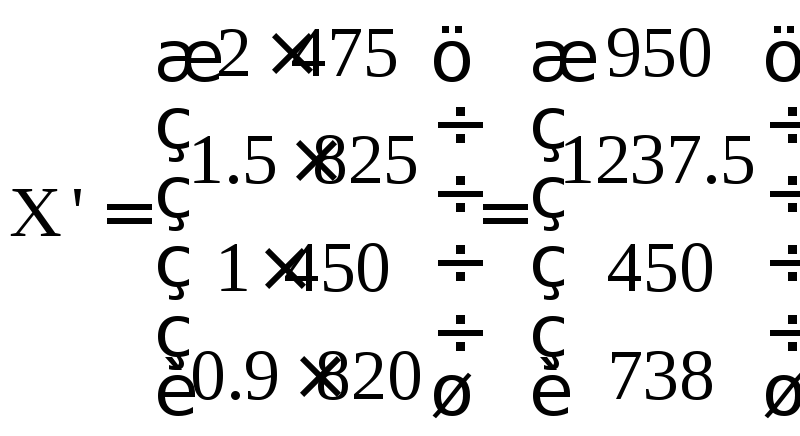 .
.
Конечный продукт отраслей:
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
