3.4. Монополия

В случае монополии фирма сама выбирает цену, исходя из кривой спроса на ее продукцию. Поэтому в случае фирмы-монополиста при решении задачи о максимизации прибыли с помощью функции кривых издержек будем иметь:

(51)

Оптимальный уровень выпуска найдется из условия:

или .

Поскольку - убывающая функция, то(объемqувеличивается, ценападает). При той же функции издержек, что и в предыдущем случае, графики суммарных, средних и предельных показателей показаны на рис. 14 и 15. При этом графики суммарных, средних и предельных издержек имеют тот же вид, что и в предыдущем случае.

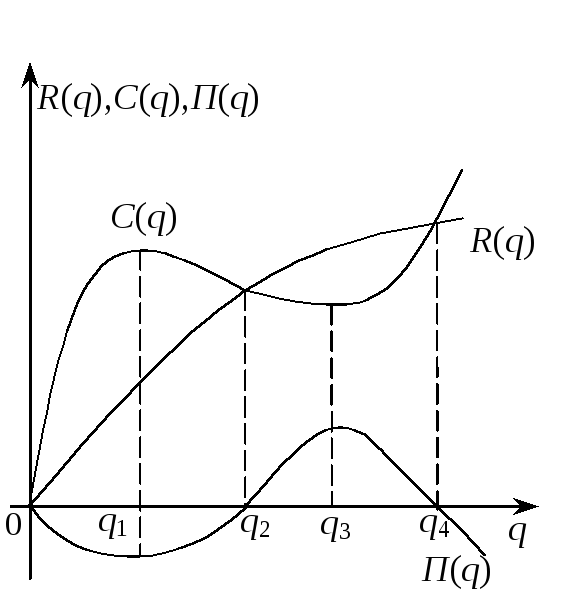
Рис. 14. Максимизация прибыли Рис. 15. Максимизация прибыли

в условиях «чистой» монополии

График среднего дохода совпадает с графиком функции спроса и пересекает график средних издержекАСв точкахи(где). График предельного доходаMRлежит ниже графика среднего доходаARпри любых объемах выпуска, так как

,

(поскольку ), и пересекает график предельных издержек в точкахи, в которых касательные к графикам дохода и издержек имеют одинаковый наклон. При этих объемах выпуска прибыль, как и в предыдущем случае, принимает минимальное и максимальное значения соответственно. Это обусловлено тем, что необходимое условие максимума прибыли по-прежнему записывается как, и в оптимальной точке предельный доход обязательно равен предельным издержкам:.

Аналогично предыдущему случаю, прибыль на графиках средних и предельных величин также можно определить как площадь заштрихованного прямоугольника, построенного между графиками среднего дохода и средних издержек (вершины прямоугольника находятся в точках:.

Порядок построения графика 15:

1. Строим MCиMR.

(абсцисса - при которой получаем минимум прибыли);

(абсцисса - при которой получаем максимум прибыли:).

2. Строим AR.

ARиMR имеют общую абсциссу 0, прямаяARвыше прямойMR.

3. Строим АС.

4. Пересечение перпендикуляра из точки с прямойARдает значение. Точкаесть точка экстремума, максимума прибыли.

5. Пересечение перпендикуляра из точки с кривойАСдает значение.

- общий максимальный доход фирмы;

- общие минимальные издержки фирмы;

- максимальная прибыль фирмы.

Итак, при определении оптимального объема производства фирмы, если известны ее функции суммарного дохода и издержек и(предполагается, что эти функции дифференцируемы), средние и предельные показатели могут быть использованы следующим образом.

Вначале находятся точки, в которых величина предельного дохода равна величине предельных издержек: . Если таких точек нет, то фирме либо невыгодно производить вообще (при<), либо выгодно сколь угодно наращивать объем производства (при>).

В найденных точках может достигаться максимум прибыли, максимум убытка, минимум прибыли, минимум убытка, либо ничего из перечисленного.

Поэтому далее среди этих точек находятся те, в которых функция прибыли достигает максимума (ее производная меняет знак с плюса на минус). Это точки максимума прибыли или минимума убытка.

Наконец, нужно выбрать точки (точку), где величина прибыли положительная. Признаком этого может быть превышение среднего дохода над средними издержками: . Если такая точка найдена, то она является точкой (локального) максимума прибыли фирмы.