3.2. Несовершенная конкуренция

В случае несовершенной конкуренции фирма имеет возможность влиять на цену продукции путем варьирования выпуска своей продукции (монополия), либо на цену затрат путем варьирования своих покупок данного вида затрат (монопсония), так что

,

.

Тогда задача фирмы в условиях несовершенной конкуренции может быть представлена в виде:

(48)

где есть производственная функция (выпуск фирмы).

3.3. Совершенная конкуренция

В условиях совершенной конкуренции цена на единицу продукции фирмы не зависит от объема производства qданной фирмы, а определяется рынком и постоянна, то есть.

Следовательно, доход фирмы будет равен доход фирмы является линейной функцией объема выпускаq.

Прибыль фирмы

. (49)

Графики этой функции фирмы где - издержки фирмы, зависящие от объема выпускаqи растущие быстрее, чем доход при малых объемах выпуска, показаны на рис. 14 и 15.

Рис. 14. Определение оптимального выпуска через совокупный доход и кривые издержек в условиях совершенной конкуренции

Пояснения к построению графика на рис. 14.

1. В основе построения графика функции фирмы лежит формула прибыли фирмы: .

2. Строим график функции - это прямая, проходящая через начало системы координат.

3. Строим - общие издержки, зависящие от объема выпускаq:

сначала издержки превышают доходы(>при; их максимум при). Это выпуклая вверх часть графика- находится над.

Затем издержки становятся меньше доходовпри. Это выпуклая вниз часть графика- находится под. Их минимум при.

В итоге получаем волну, огибающую .

4. Строим график - это волна, огибающая осьОq.

В условиях совершенной конкуренции оптимальный уровень выпуска является решением задачи

Необходимое условие экстремума функции (условие первого порядка), чтобы производная прибыли Ппо переменнойqравнялась нулю:

. (50)

Решение уравнения (50) приводит к тому, что цена единицы выпуска равняется предельным издержкам:

.

Достаточное условие экстремума функции (условие второго порядка) утверждает, что предельные издержки должны возрастать в этой точке:

то есть кривая МС– вогнута (выпукла вниз).

Поэтому оптимальный выпуск (см. рис. 15) находится в точке и характеризует оптимальный уровень предложения выпуска при цене выпускаи заданной функции издержек.

Для типичной функции издержек (растущих быстрее, чем доход при малых объемах выпуска) графики дохода, издержек и прибыли показаны на рис.15.

На нем построены графики средних и предельных величин. Так как , то графики среднего и предельного дохода имеют вид прямой, параллельной оси 0q.

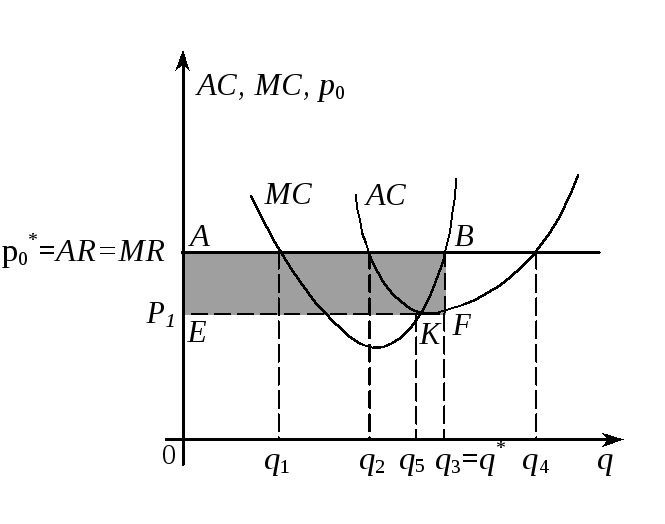
Рис. 15. Определение оптимального выпуска через совокупный доход и кривые издержек в случае совершенной конкуренции

График средних издержек АСсовпадает с графиком среднего доходаARпри объемах выпускаи(так как в этих точках значения функцийисовпадают); лежит выше него прии(из>) и ниже – при. В точкес абсциссойи ординатойиздержкиминимальны.

В точках икасательная к графикупараллельна графику дохода. Следовательно, в этих точках предельные издержки совпадают с предельным доходом, и имеет место минимум прибыли (максимум убытков) в точкеи максимум прибыли (минимум убытков) в точке(, поскольку, как видно из рис. 14, прибыль положительна при объеме выпускаи отрицательна прии). Величину прибыли при оптимальном объеме выпуска () можно найти как площадь заштрихованного прямоугольникаABFEпо графикам средних издержек и среднего дохода. Вершины прямоугольника находятся в точках с координатами:.

Площадь прямоугольника - это общий доход фирмы

.

Площадь прямоугольника - это минимальные издержки:

.

Тогда площадь прямоугольника ABFEесть максимум прибыли, то есть

.