
- •Математическая экономика
- •230700 «Прикладная информатика»
- •Содержание
- •Предисловие
- •1.Модельповедения потребителя
- •Предпочтения потребителей
- •1.2. Функция полезности
- •1.3. Поверхности и кривые безразличия
- •1.4. Предельный анализ и эластичность
- •Перекрестная эластичность спроса по цене
- •Эластичность спроса по доходу
- •Предельная норма замещения
- •1.5. Модель поведения потребителя
- •1.6. Геометрическая интерпретация задачи максимизации полезности
- •1.7. Аналитическое решение задачи максимизации полезности
- •I способ. Приведение функции к одной переменной
- •II способ. Использование функции Лагранжа
- •1.8. Эффект компенсации. Уравнение Слуцкого
- •2. Модель поведения производителей
- •2.1. Производственная функция
- •2.2. Реакция производителей на изменение условий
- •2.3. Функции издержек
- •Задача на минимизацию издержек
- •2.4. Модели установления равновесной цены Дискретная паутинообразная модель рынка с запаздыванием предложения
- •Модель спроса и предложения Гудвина
- •Паутинообразная модель
- •Модель Эванса
- •3. Модели поведения фирмы на конкурентных рынках
- •3.1. Построение модели
- •3.2. Несовершенная конкуренция
- •3.3. Совершенная конкуренция
- •3.4. Монополия
- •3.5. Задача на максимизацию прибыли
- •4. Модель Леонтьева многоотраслевой экономики
- •4.1. Балансовые соотношения
- •4.2. Линейная модель многоотраслевой экономики
- •4.3. Продуктивные модели Леонтьева
- •Вопросы для самоконтроля
- •Список литературы
- •Математическая экономика
- •230700 «Прикладная информатика»
- •650992, Г. Кемерово, пр. Кузнецкий, 39
Модель Эванса
В модели Эванса рассматривается рынок одного товара. Время t считается непрерывным.
Введем обозначения:
![]() -
цена единицы товара в момент времени
t;
-
цена единицы товара в момент времени
t;
![]() -
совокупный спрос в момент времени t;
-
совокупный спрос в момент времени t;
![]() -
совокупное предложение в момент времени
t.
-
совокупное предложение в момент времени
t.
Предполагается, что спрос и предложение являются линейными функциями цены:
![]() ,
(
,
(![]() ,
,![]() ,
спрос с ростом цены убывает)
,
спрос с ростом цены убывает)
![]() ,
(
,
(![]() ,
,
![]() ,
предложение с ростом цены растет).
,
предложение с ростом цены растет).
Естественно
считать, что
![]() (так как при нулевой цене спрос превышает
предложение).
(так как при нулевой цене спрос превышает
предложение).
Итак,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Основное предположение модели состоит в том, что изменение цены пропорционально превышению спроса над предложением:
![]() ,
,
![]() .
(43)
.
(43)
Из равенства (43) следует, что потребители и производители взаимодействуют так, чтобы цена непрерывно приспосабливалась к ситуации на рынке. В случае превышения спроса над предложением цена возрастает, в противном случае – падает.
Чтобы
иметь равновесную цену, спрос должен
равняться предложению. Из
![]() следует, что
следует, что
![]() ,
,
![]() ,
,
![]() -
стационарная равновесная точка.
-
стационарная равновесная точка.
Равновесная
цена
![]() есть абсцисса точки пересечения прямых
спроса и предложения.
есть абсцисса точки пересечения прямых
спроса и предложения.
Примечание.
Из
![]() ,
,![]() ,
t
– непрерывно
следует, что
,
t
– непрерывно
следует, что
![]() или
или
![]() .
.
Если
![]() ,
,![]() ,
то
,
то![]() и
и![]() ,
,
или
![]() ,
,
![]() (44)
(44)
есть дифференциальное уравнение первого порядка.
Решение.
Метод подстановки:
 ;
; ;
;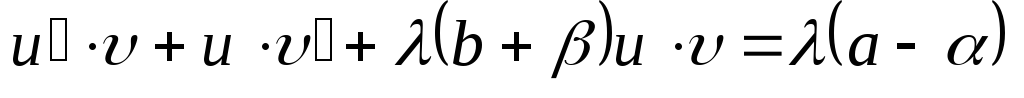 ;
; ;
; ;
;
 ;
; ;
;
 ;
; ;
; ;
;
![]() ;
;
![]() ;
;
 ;
; ;
;
 ;
; ;
;Вычислим частное значение С при
 ,
, :
:
![]() ;
;
![]() .
.
Окончательный ответ:
![]() .
.

Рис.13. Дискретный аналог модели Эванса
Решением дифференциального уравнения (44) является формула вычисления цены р в момент времени t:
![]() .
.
Дискретный аналог модели Эванса представлен на рис. 13.
На
рисунке 13 изображены прямые совокупного
спроса и предложения и показан механизм
возникновения последовательности
![]() ,
возрастающей от начальной цены
,
возрастающей от начальной цены![]() ,
при которой спрос не равен предложению,
к равновесной цене
,
при которой спрос не равен предложению,
к равновесной цене![]() ,
при которой спрос равен предложению.
,
при которой спрос равен предложению.
Все
время разбито на интервалы длиной
![]() ,
цена в момент
,
цена в момент![]() равна
равна
![]() ,
,
где
![]() .
.
3. Модели поведения фирмы на конкурентных рынках
3.1. Построение модели
Пусть
![]() ,
,
![]() ,
- вектор объемов затрачиваемых фирмой
ресурсов (факторов производства),
,
- вектор объемов затрачиваемых фирмой
ресурсов (факторов производства),
![]() ,
,
![]() ,
- вектор рыночных цен на соответствующие
ресурсы,
,
- вектор рыночных цен на соответствующие
ресурсы,
![]() - производственная
функция фирмы, которая выражает общий
объем qпродукции
выпускаемой фирмой, используя
- производственная
функция фирмы, которая выражает общий
объем qпродукции
выпускаемой фирмой, используя
![]() ресурсов,
ресурсов,
![]() - рыночная цена
единицы выпуска фирмы.
- рыночная цена
единицы выпуска фирмы.
Рассмотрим такие понятия как доход, издержки, прибыль фирмы.
Доходом(выручкой)Rфирмы в
определенном временном периоде
(например, в определенном году) называется
произведение
![]() общего объемаqвыпускаемой фирмой продукции на рыночную
цену
общего объемаqвыпускаемой фирмой продукции на рыночную
цену
![]() единицы этой продукции.
единицы этой продукции.
ИздержкамиСфирмы называют общие выплаты фирмы в определенном временном периоде за все виды затрат, например,
![]() ,
,
где х1их2– объемы затрачиваемых (используемых) фирмой ресурсов (факторов производства),
р1ир2– рыночные цены соответственно на эти ресурсы (факторы производства).
ПрибыльюПфирмы в определенном временном периоде называется разность между полученным доходомRи ее издержками производстваС, т.е.
![]()
![]() .
(45)
.
(45)
Последнее равенство есть выражение прибыли фирмы в терминах затрачиваемых (используемых) ресурсов.
В теории фирмы принято считать, что если фирма функционирует в условиях чистой (совершенной) конкуренции, на рыночные цены р0,р1ир2 она влиять не может. Фирма «соглашается» с ценамир0,р1ир2. Случаи функционирования фирмы в условиях чистой монополии, монополистической конкуренции и олигополии специально рассматриваются в рамках курса по микроэкономике.
Неоклассическая
теория фирмы построена на предположении,
что цель фирмы заключается в максимизации
прибыли путем выбора комбинации
количеств затрат при заданных
производственной функцией
![]() ,
рыночной цене единицы выпускар0и ценах затрат
,
рыночной цене единицы выпускар0и ценах затрат![]() .
.
Формально
задача максимизации прибыли в определенном
периоде имеет вид:
![]() .
.
Такая постановка задачи максимизации зависит от того, какой конкретно временной промежуток (долговременный или краткосрочный) предшествует периоду, в котором фирма максимизирует свою прибыль.
Итак, с точки зрения временного промежутка можно различать задачи двух типов:
задача текущего производства (краткосрочная задача);
задача перспективного развития (долгосрочная задача).
Краткосрочная задача. Эта задача планируется с учетомналичных запасов ресурсов на данный период, которые формально могут быть записаны, вообще говоря, в виде нелинейного неравенства
![]()
(ограничений
вида
![]() может быть несколько); с постоянными
рыночными ценами на эти ресурсы. Исходя
из этих условий, модель задачи строится
на условную оптимизацию:
может быть несколько); с постоянными
рыночными ценами на эти ресурсы. Исходя
из этих условий, модель задачи строится
на условную оптимизацию:
![]()
при условии, что
![]() ,
,
![]() ,
,
![]() .
.
Решая долгосрочную задачу, фирма может выбрать любой вектор затрат, поэтому оптимальная стратегия фирмы сводится к решению задачи:
 (46)
(46)
Оптимальный
вектор затрат
![]() решения задачи (46) будет, естественно,
зависеть от заданных цен на продукцию
и цен на ресурсы, то есть является
функциейр0и
решения задачи (46) будет, естественно,
зависеть от заданных цен на продукцию
и цен на ресурсы, то есть является
функциейр0и
![]() :
:
![]() ,
(47)
,
(47)
где
компоненты вектора
![]() есть
есть

Функция (46) носит название функции спроса на затраты.
Подставим
функцию спроса на затраты в производственную
функцию. Получим выпуск как функцию
аргументов р0и
![]()
![]() .
.
Тем самым получаем объем продукции фирмы, который отвечает ее рациональной стратегии и носит название функции предложения фирмы.
