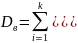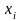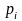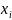Теория вероятности Вариант 45
.docxГрафики построены с использованием сайта math.semestr.ru.
1.
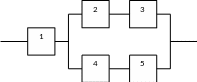
Электрическая цепь состоит из пяти
элементов, выход из строя которых в
заданный промежуток времени – независимые
события, имеющие вероятности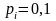 каждый. Найти вероятность
каждый. Найти вероятность
 отказа цепи за данный промежуток времени.
отказа цепи за данный промежуток времени.
Решение:
По
условию
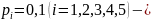 вероятности
выхода из строя пяти элементов.
вероятности
выхода из строя пяти элементов.
Найдем
вероятность работы всей цепи при
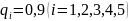
При последовательном соединении:

Та же самая вероятность отказа будет на участке 4-5:

При параллельном соединении:
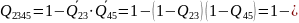
Окончательно при последовательном соединении:
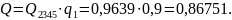
Тогда вероятность отказа всей цепи:
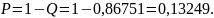
2. Дискретная случайная величина задана
законом распределения
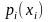 .
Найти величину
.
Найти величину
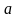 ,
построить график функции распределения
данной случайной величины. Вычислить
математическое ожидание, дисперсию и
среднее квадратическое отклонение
данной случайной величины.
,
построить график функции распределения
данной случайной величины. Вычислить
математическое ожидание, дисперсию и
среднее квадратическое отклонение
данной случайной величины.
|
0 |
2 |
4 |
6 |
8 |
|
|
0,2 |
0,4 |
0,2 |
0,1 |
Решение:
Величину a находим из условия:
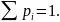
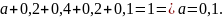
|
0 |
2 |
4 |
6 |
8 |
|
0,1 |
0,2 |
0,4 |
0,2 |
0,1 |
Построим график распределения случайной величины.
При
х 0,
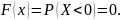
При
0 < х 2,
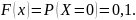
При
2 < х 4,

При
4 < х 6,

При
6 < х 8,

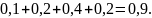
При
х >8,
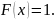
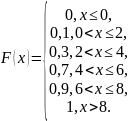
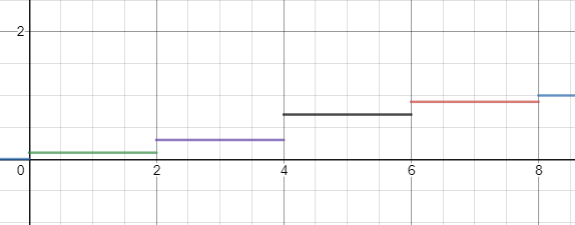
Вычислим математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины.
|
0 |
2 |
4 |
6 |
8 |
|
0,1 |
0,2 |
0,4 |
0,2 |
0,1 |
Математическое ожидание:
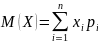
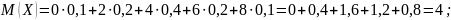
Дисперсия:


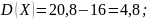
Среднее квадратическое отклонение:
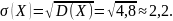
3. Плотность распределения вероятностей непрерывной случайной величины задана выражением:

Найти
величину коэффициента
,
написать аналитическое выражение и
простроить график функции распределения,
найти математическое ожидание, дисперсию
и среднее квадратическое отклонение
данной случайной величины. Найти
вероятности попадания данной случайной
величины в интервалы
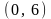 и
и
 .
.
Решение:
Величину коэффициента a находим по свойству функции распределения:


Тогда
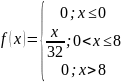
Найдем функцию распределения:
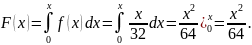
Тогда

График функции распределения вероятности:

Найдем математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины.
Математическое ожидание:
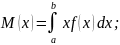

Дисперсия:
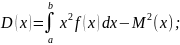
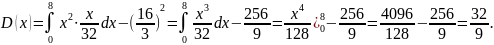
Среднее квадратическое отклонение:
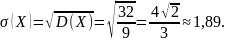
Найдем вероятности попадания данной случайной величины в интервалы и .

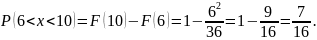
4. Вероятность попадания нормально
распределенной случайной величины с
математическим ожиданием
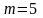 в интервал (4; 6) равна 0,8. Найти дисперсию
данной случайной величины.
в интервал (4; 6) равна 0,8. Найти дисперсию
данной случайной величины.
Решение:
Для нормально распределенной случайно величины выполняется следующее:


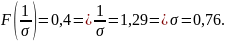
Дисперсия:
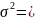
5. Дискретная случайная величина задана выборкой:
1, 2, 3, 3, 3, 3, 3, 1, 1, 1, 2, 3, 3, 1, 1, 1, 1, 3, 3, 1, 1, 1, 2, 3, 1
Построить полигон частот и эмпирическую функцию распределения. Найти выборочное среднее и выборочную дисперсию.
Решение:
Построим вариационный ряд: отсортируем выборку в порядке возрастания.
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3
Построим статистический ряд распределения:
|
1 |
2 |
3 |
|
12 |
3 |
10 |
n = 25 – объем выборки.
Построим полигон частот:
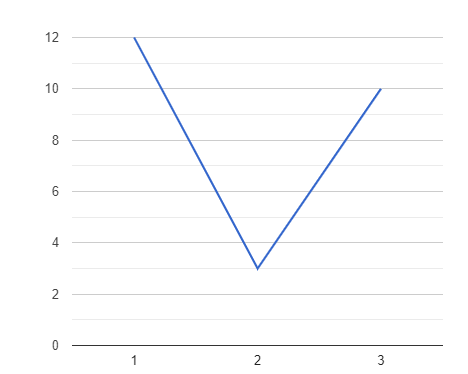
Найдем эмпирическую функцию распределения:
При х 1,
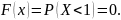
При 1 < х 2,

При 2 < х 3,

При х > 3,
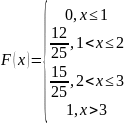
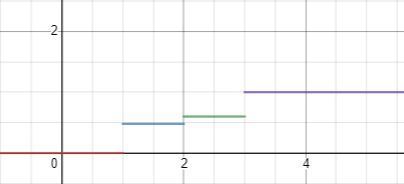
Найдем выборочное среднее и выборочную дисперсию.
Выборочная средняя:

Выборочная дисперсия: