6. Основные уравнения гидродинамики

Гидродинамика – раздел гидравлики, изучающий законы движения жидкости и ее взаимодействия с неподвижными и подвижными поверхностями.

Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.

В целях упрощения расчета вводится понятие струйчатой модели движения. Согласно этой модели поток состоит из отдельных элементарных струек, изучение которых в отдельности дает возможность понять закономерности потока в целом.

Основными уравнениями гидродинамики являются уравнение неразрывности (сплошности) и уравнение Бернулли.

Уравнение неразрывности есть уравнение постоянства расхода.

1. Для элементарной струйки

или

,

где U₁, U₂, U – скорости движения частиц жидкости в отдельных живых сечениях струйки; d₁, d₂, d - площади живых сечений струйки.

2. Для потока

или

,

где V₁, V₂, V – средние скорости в живых сечениях; ₁, ₂,  - площади живых сечений потока.

Уравнение Бернулли является фундаментальным уравнением гидродинамики. Оно устанавливает связь между давлением, скоростью и положением жидкости в пространстве. С помощью этого уравнения решается большой круг инженерных задач.

Для упрощения изучения общих закономерностей, присущих особенно движущейся жидкости, ее часто представляют в виде несжимаемой среды, не обладающей внутренним трением. Такую жидкость называют идеальной.

Уравнение Бернулли для элементарной струйки идеальной жидкости

Расчетная форма этого уравнения имеет вид

,

где Z – геометрический напор, или удельная потенциальная энергия положения; – пьезометрический напор, или удельная потенциальная энергия давления; – скоростной напор, или удельная кинетическая энергия.

П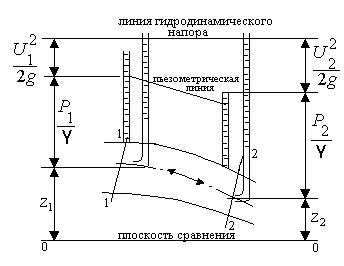 редставим это уравнение графически для элементарной струйки переменного сечения (см рис.1)

Рис.1.

Это уравнение является уравнением закона сохранения энергии для движущейся жидкости. В этом заключается его физический смысл.

Уравнение Бернулли для элементарной струйки реальной жидкости

При движении реальной жидкости, обладающей вязкостью, часть ее энергии затрачивается на преодоление сил трения. Эта энергия в виде тепла рассеивается в окружающую среду. Процесс этот необратим и в физике называется диссипацией. Диссипируемую энергию в гидравлике называют гидравлическими потерями.

Расчетную форму уравнения Бернулли для элементарной струйки реальной жидкости можно представить в виде

,

где h_п – гидравлические потери.

Г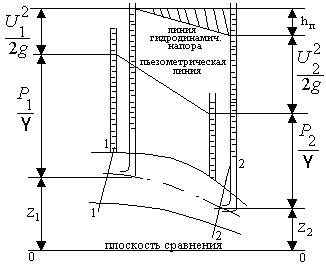 рафик этого уравнения показан на рисунке 2.

Рис.2.

Уравнение Бернулли для потока реальной жидкости

Так как поток представляется совокупностью элементарных струек, то его энергия будет равна их сумме.

При плавно изменяющемся движении потенциальную энергию для каждой струйки можно считать величиной постоянной, а действительная кинетическая энергия потока будет несколько больше по сравнению с кинетической энергией, подсчитанной по средней скорости, поэтому для компенсации этого неравенства вводится скоростной коэффициент (коэффициент Кориолиса).

Таким образом, уравнение Бернулли для потока реальной жидкости имеет вид

,

где  - коэффициент Кориолиса, он зависит от режима движения жидкости.

Для ламинарного движения при Re  2320  = 2; для турбулентного при Re  2320  = 1,05…1,1  1,0.