
- •Федеральное агентство связи
- •Работа № 1. Сигналы и их спектры Исполнитель Иванов и.И. Гр. Икт-100 (10.07.12)
- •1. Исследование зависимости спектра сигнала от его формы.
- •А б
- •1. Исследование сигналов
- •Работа 1. Сигналы и их спектры
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Контрольные вопросы
- •Работа 2. Аналитический сигнал
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Контрольные вопросы
- •Работа 3. Дискретизация и восстановление сигналов
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Контрольные вопросы
- •Работа 4. Модулированные сигналы
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Работа 5. Ортогональность сигналов
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •2. Нелинейные преобразования сигналов
- •А) б) в)
- •Г) д)
- •Характеристик нп Работа 6. Преобразование сигналов в нелинейных цепях
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Работа 7. Нелинейное усиление и умножение частоты
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Работа 8. Амплитудная модуляция
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Контрольные вопросы
- •Работа 9. Детектирование ам сигналов
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Работа 10. Преобразование частоты сигналов на нелинейной основе
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Параметрические преобразования сигналов
- •Работа 11. Линейные виды модуляции
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Контрольные вопросы
- •Работа 12. Преобразование частоты на параметрической основе
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Работа 13. Детектирование фм и чм сигналов
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Системы передачи дискретных сообщений
- •Работа 14. Знакомство с системой пдс
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Контрольные вопросы
- •Работа 15. Исследование когерентных демодуляторов
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Контрольные вопросы
- •Работа 16. Исследование некогерентных демодуляторов
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Контрольные вопросы
- •Работа 17. Исследование помехоустойчивости спдс
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Контрольные вопросы
- •Работа 18. Помехоустойчивое кодирование в спдс
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Статистическая радиотехника
- •Работа 19. Законы распределения случайных процессов
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Контрольные вопросы
- •Работа 20. Прохождение случайных процессов через фу
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Контрольные вопросы
- •Работа 21. Детектор огибающей сигнала
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Работа 22. Согласованная фильтрация сигналов
- •З Рис. 40. Набор сф Рис. 41. Двоичный тф Рис. 42. Аналоговый тФадание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Контрольные вопросы
- •Цифровые виды модуляции в системах связи
- •Работа 23. Передача непрерывных сообщений по цифровому каналу
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Работа 24. Исследование ацп и цап
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Работа 25. Исследование сигналов с фм и офм
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Работа 26. Исследование сигналов с фм-4 (qpsk и oqpsk)
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Работа 27. Исследование сигналов с фм-16
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Работа 28. Исследование сигналов с кам-16 (qask и spm)
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Работа 29. Исследование сверточного кодирования, цм и скк
- •З Рис. 54. Форма с решетчатой диаграммой выживших путей декодера Витербиадание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Создание и выполнение альтернативных лабораторных работ
- •Перечень ресурсов виртуальной лаборатории
- •Пример оформления отчета в редакторе ms Word с использованием скриншотов и других файлов, записанных в лаборатории на дискету или флешку
- •Литература
- •Содержание
Работа 2. Аналитический сигнал
Работа «Аналитический сигнал» предназначена для изучения временных и спектральных характеристик компонентов сигналов, представленных в квазигармонической форме.
Она содержит шесть заданий:
Исследование спектральных характеристик сигнала и его преобразования по Гильберту.
Исследование квадратурных компонентов, огибающей и фазы прямоугольных видеоимпульсов.
Исследование связи гармонического модулирующего сигнала с огибающей модулированного по амплитуде сигнала.
Исследование связи гармонического модулирующего сигнала с огибающими двухполосного (БМ) и однополосного (ОМ) сигналов.
Повторение задания 3 при прямоугольной форме модулирующих импульсов.
Повторение задания 4 при прямоугольной форме модулирующих импульсов.
При выборе данной работы генератор сигналов (рис. 14), выводимый на лабораторный стол, дополняется блоком «Компоненты аналитического сигнала» (рис. 17). Этот блок содержит: преобразователь Гильберта «H[u]», квадраторы «КВ», делитель «ũ/u» сигнала ũ = H[u(t)] на сигнал u(t), сумматор сигналов «Σ», вычислители косинусного «Ac(t)» и синусного «As(t)» компонентов, фазы «Ф(t)» и огибающей «A(t)» входного сигнала u(t). Десятикнопочный переключатель служит для подключения измерительных каналов к отдельным узлам блока. На вход 1 всегда поступает сигнал u(t) от генератора, описанного в работе 1.
Рис. 17.
Компоненты аналитического сигнала
Задание 1
Исследуйте связи амплитудных (АС) и фазовых (ФС) спектров сигналов до и после их преобразования по Гильберту. В качестве исходного сигнала используйте импульсы прямоугольной формы без постоянной составляющей с размахом А = 1 В, частотой следования 1 кГц, длительностью dT = 0,2 мс.
Наблюдайте и зафиксируйте осциллограммы и спектрограммы сигналов в следующей последовательности по каналам:
1) исходный сигнал u(t) и его АС (т. 1);
2) преобразованный H[u(t)] и его АС (т. 2);
3) исходный сигнал u(t) и его ФС (т. 1);
4) преобразованный H[u(t)] и его ФС (т. 2).
Для вывода фазового спектра активизируйте пункты меню «Параметры АС» / «Фазовый спектр и ФЧХ».
Сделайте выводы по результатам наблюдений.
Комментарии и выводы
В результате преобразования сигнала по Гильберту его амплитудный спектр S(ω) сохраняется, а фазовый спектр Ψ(ω) изменяется на –90˚ в области положительных частот и на +90˚ в области отрицательных частот.
Это соответствует характеристикам преобразователя Гильберта:
передаточной функции H(jω) = –jsign(ω), АЧХ H(ω) = 1 и ФЧХ
![]()
Задание 2
В продолжение задания 1 исследуйте связи между формой, амплитудным спектром сигнала u(t), с одной стороны, и его косинусным Ac(t), синусным As(t) квадратурными компонентами и огибающей A(t), с другой.
В качестве исходного сигнала u(t) оставьте импульсы прямоугольной формы без постоянной составляющей с размахом А = 1 В, частотой следования 1 кГц, длительностью dT = 0,2 мс.
Наблюдайте и зафиксируйте осциллограммы и спектрограммы в следующей последовательности по каналам:
1) косинусный компонент Ac(t) (т. 7);
2) синусный компонент As(t) (т. 8);
3) огибающая сигнала A(t) (т. 10);
4) фаза сигнала Ф(t) (т. 9).
Сделайте выводы по результатам наблюдений.
Комментарии и выводы
Составляющие
квазигармонической формы сигнала
![]()
определяются следующим образом:
1) огибающая
![]() ,
,
2) полная фаза

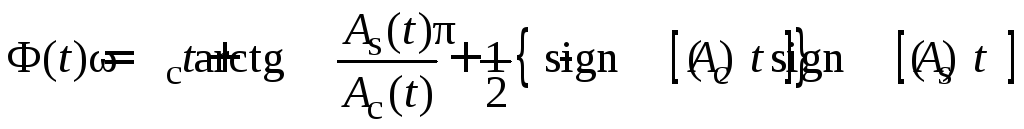 ,
,
3) косинусный квадратурный компонент
![]() ,
,
4) синусный квадратурный компонент
![]() .
.
