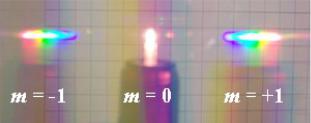
Описание явления
Фронт световой волны разбивается штрихами решётки на отдельные пучки когерентного света. Эти пучки претерпевают дифракцию на штрихах и интерферируют друг с другом. Так как для разных длин волн максимумы интерференции оказываются под разными углами (определяемыми разностью
хода интерферирующих лучей), то белый свет раскладывается в спектр. Так выглядит свет лампы накаливания фонарика,
прошедший через прозрачную дифракционную решётку.
|
|
Нулевой максимум ( |
m=0 |
) соответствует свету, |
|
|
прошедшему сквозь решётку без отклонений. В силу |
||
|
|
дисперсии решётки в первом ( m=± 1 ) максимуме |
||
|
|
можно наблюдать разложение света в спектр. Угол |
||
|
|
отклонения возрастает с ростом длины волны (от |
||
|
|
фиолетового цвета к красному) |
||
Формулы |
|
|
|
|
Расстояние, через которое повторяются штрихи на решётке, называют периодом |
||||
дифракционной решётки. Обозначают буквой d . |
|
|
||
Если известно число штрихов ( |
N |
), приходящихся на |
1 мм |
решётки, то период |
решётки находят по формуле: d=1/ N |
мм. |
|
|
|
Условия интерференционных максимумов дифракционной решётки, наблюдаемых под |
||||
определёнными углами, имеют вид: |
d sin α=k λ , где |
|
|
|
d - период решётки, |
|
|
|
|
α - угол максимума данного цвета,
k - порядок максимума, то есть порядковый номер максимума, отсчитанный от центра картинки,
λ- длина волны.
Если же свет падает на решётку под углом θ , то:
d{sin α+sinθ}=k λ
5.Поляризация света. Закон Малюса. Поляризация света при отражении. Закон Брюстера.
Поляризация света.
Поляризация света — выделение из пучка естественного света лучей, поляризованных в определенной плоскости.
Естественный свет — свет, в котором колебания вектора совершаются в самых различных направлениях, перпендикулярных лучу.
Поляризованный свет — свет, в котором колебания вектора подчинены определенному закону.
Плоско-поляризованный свет — свет, в котором колебания светового вектора происходят вдоль одной плоскости.
Плоскость поляризатора — это плоскость, которая параллельна колебаниям, которые пропускает поляризатор.
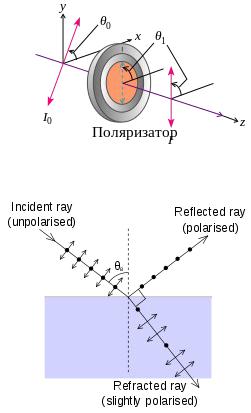
Поляризация света при отражении.
При пропускании частично-поляризованного света (колебания одного направления преобладают над колебаниями других направлений) через поляризатор интенсивность прошедшего света будет изменяться, если вращать прибор вокруг направления луча.
При повороте на ϕ=π/2 |
интенсивность изменяется от J max до J min . |
||
Количественной характеристикой является степень поляризации: |
|||
P= |
Jmax−Jmin |
. |
|
|
Jmax+Jmin |
|
|
Для естественного света |
J max=J min , P=0 . Для плоско поляризованного света , |
||
J min=0 , P=1 |
|
||
При падении света на границу раздела двух диэлектриков и отраженный, и преломленный лучи оказываются частично поляризованными. В отраженном луче преобладают колебания E , перпендикулярные плоскости падения, в преломленном – колебания, параллельные плоскости падения.
Закон Малюса.
Закон Малюса — физический закон, выражающий зависимость интенсивности линейно-поляризованного света после его прохождения через поляризатор от угла ϕ между плоскостями поляризации падающего света и поляризатора.
I=ka I0 cos2 ϕ , где
I0 — интенсивность падающего на поляризатор
света,
I — интенсивность света, выходящего из поляризатора,
ka — коэффициент пропускания поляризатора.
Закон Брюстера.
Закон Брюстера — закон оптики, выражающий связь показателей преломления двух диэлектриков с таким углом падения света, при котором свет, отражённый от границы раздела диэлектриков, будет полностью поляризованным в плоскости, перпендикулярной плоскости падения. При этом преломлённый луч частично поляризуется в плоскости падения, и его поляризация достигает наибольшего значения. Угол падения, при котором отражённый луч полностью поляризован, называется углом Брюстера. При падении под углом Брюстера отражённый и преломлённый лучи взаимно перпендикулярны.
Закон Брюстера записывается в виде:
tgθBr=n21 , где n21=n2 /n1 — показатель преломления второй среды относительно первой, а
θBr — угол падения (угол Брюстера).
Иллюстрация поляризации отражённого света, падающего на границу раздела сред под углом Брюстера
6. Характеристики теплового излучения. Закон Кирхгофа. Закономерности излучения абсолютно чёрного тела. Законы Стефана-Больцмана и закон Вина. Ультрафиолетовая катастрофа. Гипотеза и формула Планка. Фотон, энергия, масса и импульс фотона. Корпускулярно-волновой дуализм. Световое давление. Фотоэффект и его законы, вольтамперная характеристика, уравнение Эйнштейна.
Характеристики теплового излучения
•Энергетическая светимость тела - RT — физическая величина, являющаяся функцией температуры и численно равная энергии, испускаемой телом в единицу времени с единицы площади поверхности по всем направлениям и по всему спектру частот.
RT = |
dW |
; [RT ]= Дж/с м2=Вт/ м2 |
|
dt dS |
|||
|
|
•Спектральная плотность энергетической светимости — функция частоты и температуры, характеризующая распределение энергии излучения по всему спектру
частот (или длин волн).
∞
RT =∫rω ,T d ω
0
•Поглощающая способность тела — aω , T — функция частоты и температуры,
показывающая, какая часть энергии электромагнитного излучения, падающего на
тело, поглощается телом в области частот d ω вблизи |
ω |
|||
aω , T= |
d Φ'ω, T |
, |
|
|
|
|
|||
|
|
d Φω, T |
|
|
где |
d Φ' — поток энергии, поглощающейся телом. |
|
||
d Φ |
— поток энергии, падающий на тело в области |
d ω вблизи ω |
||
•Отражающая способность тела — bω , T — функция частоты и температуры,
показывающая какая часть энергии электромагнитного излучения, падающего на тело, отражается от него в области частот d ω вблизи ω
b |
= d Φ' 'ω, T |
, |
|
ω , T |
|
d Φω, T |
|
|
|
|
|
где |
d Φ' ' — поток энергии, отражающейся от тела. |
||
d Φ |
— поток энергии, падающий на тело в области d ω вблизи ω |
||
•Абсолютно черное тело — это физическая абстракция (модель), под которой
понимают тело, полностью поглощающее всё падающее на него электромагнитное излучение
aω , T=1 — для абсолютно чёрного тела
•Серое тело — это такое тело, коэффициент поглощения которого не зависит от
частоты, а зависит только от температуры aω , T=aT <1 — для серого тела
•Объемная плотность энергии излучения — UT — функция температуры, численно равная энергии электромагнитного излучения в единицу объёма по всему спектру частот
•Спектральная плотность энергии — Uω ,T — функция частоты и температуры,
связанная с объемной плотностью излучения формулой:
∞
UT =∫Uω ,T d ω
0
Следует отметить, что спектральная плотность энергетической светимости для абсолютно чёрного тела связана со спектральной плотностью энергии следующим соотношением:
rω ,T =f (ω ,T )= 4c U ω, T — для абсолютно чёрного тела
Закон Кирхгофа
Отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты и не зависит от их формы и химической природы.
f (ω,T )= r(ω,T ) a(ω,T )
Закономерности излучения абсолютно чёрного тела
Абсолютно черным называется тело, которое полностью поглощает все падающие на него лучи.
Для абсолютно черного тела r (w ,T )= f (w ,T ) . Таким образом, функция Кирхгофа – это лучеиспускательная способность абсолютно черного тела. При этом энергетическая
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
светимость абсолютно черного тела R(w ,T )=∫r (w ,T )dw . |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
Законы Стефана-Больцмана и закон Вина |
|
|
|
|||||||||||
|
Закон Стефана-Больцмана — закон излучения абсолютно чёрного тела. Определяет |
|||||||||||||
зависимость мощности излучения абсолютно чёрного тела от его температуры. |
||||||||||||||
|
Формулировка закона: |
|
|
|
|
|
|
|||||||
|
Мощность излучения абсолютно чёрного тела прямо пропорциональна площади |
|||||||||||||
поверхности и четвёртой степени температуры тела: |
|
|
||||||||||||
|
R=σ T4 |
|
|
|
|
|
|
|
|
|||||
|
При помощи закона Планка для излучения, постоянную σ можно определить как |
|||||||||||||
σ= |
π2 k4 |
|
|
, |
|
— постоянная Планка, k |
|
— постоянная Больцмана, |
c — скорость |
|||||
|
2 |
|
3 |
|
||||||||||
|
60 c |
|
|
|
|
|
|
|
|
|
|
|
||
света. Численное значение σ=5.670400 10−8 Дж c−1 м−2 К−4 |
|
|
||||||||||||
Общий вид закона смещения Вина |
|
|
|
|
|
|
||||||||
|
λ |
max |
= |
b |
≈0.002898 м К T−1 (К ) , где |
T |
— температура, а λ |
max |
— длина волны с |
|||||
|
T |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
максимальной интенсивностью. Коэффициент |
|
b , называемый постоянной Вина, в системе |
||||||||||||
СИ имеет значение |
0,002898 м· К . |
|
|
|
|
|
|
|||||||
Ультрафиолетовая катастрофа |
|
|
|
|
|
|
||||||||
|
Формула Рэлея-Джинса f (w ,T )= |
w2 |
|
kT |
противоречит закону Стефана-Больцмана |
|||||||||
|
4 π2 c2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и закону смещения Вина. Теоретические зависимости функции Кирхгофа от длины излучаемых электромагнитных волн удовлетворительно согласуются с экспериментальными данными лишь для больших и резко расходятся для малых.
Работы Рэлея-Джинса ясно показали, что последовательное применение классических представлений для описания теплового излучения абсолютно черного тела дает абсурдные результаты, и получили образное название «ультра-фиолетовая катастрофа».
Гипотеза и формула Планка.
Гипотеза Планка — гипотеза, выдвинутая 14 декабря 1900 года Максом Планком и заключающаяся в том, что при тепловом излучении энергия испускается и поглощается не непрерывно, а отдельными квантами (порциями). Каждая такая порция-квант имеет энергию
Ε , пропорциональную частоте ν излучения:
Ε=h ν= ω , где |
или |
= |
h |
— коэффициент пропорциональности, |
|
2π |
|||||
|
|
|
|
названный впоследствии постоянной Планка.
Формула Планка — выражение для спектральной плотности мощности излучения (Спектральной Плотности Энергетической Светимости) абсолютно чёрного тела, которое было получено Максом Планком. Для плотности энергии излучения u(ω,T ) :
|
2 |
|
ω |
|
u(ω ,T )= |
ω |
|
|
. |
2 3 |
|
ω |
||
|
π c |
|
e kT −1 |
|
Фотон, энергия, масса и импульс фотона.
Фотон — элементарная частица, квант электромагнитного излучения (в узком смысле
— света).
Фотон обладает энергией |
E=h ν= hc |
|
λ |
Фотон обладает инертной массой, которую можно найти из соотношения E=mc2
Фотон – частица, не обладающая массой покоя. Она может существовать, только двигаясь со скоростью света c .
Импульс фотона: p= k .
Корпускулярно-волновой дуализм.
Корпускулярно-волновой дуализм — принцип, согласно которому любой объект может проявлять как волновые, так и корпускулярные свойства.
Световое давление. |
|
|
|
|
|
|
|
dp |
|
|
F |
|
1 dp |
|
|
По 2-му закону Ньютона F = dt |
. Отсюда давление |
P= |
|
= |
|
dt |
. Следовательно, |
S |
S |
||||||
давление численно равно импульсу, передаваемому единице поверхности за единицу времени.
Фотоэффект и его законы.
Фотоэффект — высвобождение электронов с поверхности твердых тел или жидкостей под действием падающего света.
Законы фотоэффекта:
•фотоэффект практически безынерционен;
•существует красная граница фотоэффекта (максимальная длина волны), при которой возможен фотоэффект;
•максимальная энергия выбитых электронов не зависит от интенсивности падающего