
lektsii_TsOS_gruppa_RK_01 (1)
.pdf
|
|
2 π |
|
|
|
- 41 - |
|
|
|
|
|
|
− j |
k n |
|
|
|
|
2 π |
|
|
||
k n |
|
|
|
j |
|
k n |
|
||||
N |
|
−k n |
|
||||||||
и |
N |
- поворачивающиеся |
|||||||||
WN |
= e |
|
|
|
WN |
= e |
|
|
|
|
|
множители, |
|
которые |
являются |
периодическими |
|||||||
последовательностями с периодом N, так как |
WN(n k +m N )=W kn |
и |
|||||||||
W −( nk +mN ) = W −kn |
|
|
|
|
|
|
N |
|
|||
, где |
m = 0, ±1, |
|
. |
|
|
|
|||||
N |
|
|
N |
|
±2... |
|
|
|
|||
Если xp (n) |
является |
бесконечной |
последовательностью, то |
ее |
|||||||
ограничивают N членами и рассматривают как периодическую с периодом N, причем дискретное преобразование Фурье вычисляют
только на кратных частотах f k = k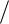 N . При этом, если имеется N
N . При этом, если имеется N
отсчетов дискретной последовательности с периодом N, то с помощью прямого дискретного преобразования Фурье можно получить N
компонент спектра на частотах f k = k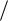 N .
N .
Например, если fд = 8 кГц , то отсчёты можно получить на
|
ˆ |
|
|
|
частотах f = 0; 1; 2;…7 кГц или f = 0; 0,125; 0,250;…0,875. |
|
|||
Непосредственное |
вычисление |
(1.4.1) |
при комплексных |
|
kn |
|
|
|
N |
значениях x(nT )*WN |
требует для |
каждого |
значения k |
|
умножений и N сложений, а для всех N значений |
k = 0, 1,..., |
N −1 |
||
требуется примерно N 2 умножений и |
N 2 сложений комплексных |
|||
чисел. Таким образом, для больших значений N (порядка нескольких сотен или тысяч) прямое вычисление ДПФ требует весьма большого числа арифметических операций умножения и сложения, что затрудняет реализацию вычисления процессов и спектров в реальном масштабе времени.
Быстрым преобразованием Фурье (БПФ) называют набор алгоритмов, реализация которых приводит к существенному уменьшению вычислений дискретного преобразования Фурье. Исходная идея этих алгоритмов состоит в том, что N-точечная последовательность разбивается на две более короткие, например на две N/2-точечные последовательности.
Вычисляются ДПФ для этих коротких последовательностей и из этих ДПФ конструируется ДПФ исходной последовательности.
Для двух N/2-точечных последовательностей требуется примерно (N/2)²·2=N²/2 умножений комплексных чисел, т.е. число
умножений (а также сложений) уменьшается примерно в 2 раза. Аналогично вместо вычисления ДПФ N/2 -точечной последовательности можно вычислить ДПФ для двух N/4-точечных
- 42 -
последовательностей и таким образом вновь уменьшить требуемое число умножений и сложений.
При N = 2v , где v > 0 и целое, процесс уменьшения размера
ДПФ может быть продолжен до тех пор, пока не останутся только двухточечные ДПФ. При этом
общее число этапов вычисления ДПФ будет равно v = log2 N , а число требуемых арифметических операций для вычисления N-точечной
N
ДПФ будет порядка N v , т.е. уменьшается примерно в log2 N раз.
Так, например, при N = 1000 для прямого вычисления ДПФ
согласно требуется примерно N 2 = 106 операций комплексных
умножений и сложений, а при использовании алгоритмов БПФ таких
операций требуется всего порядка 104 , т.е. объём вычислений
сокращается примерно на два порядка.
1.4.1. Алгоритм БПФ с прореживанием по времени.
Пусть дана последовательность длиной N = 2m , где m – целое
число. Если реальная последовательность имеет длину N ≠ 2m , то ее
дополняют отсчетами, равными нулю, так, чтобы длина результирующей последовательности была бы равна два в степени “m”.
Разобьём исходную N-точечную последовательность на две N/2-
точечные последовательности (рис.6.4.1), состоящие соответственно из чётных и нечётных членов.
N/2
N
N/2
Рис.1Основная.4.1ячейкаБПФ.
Найдем дискретное преобразование Фурье от каждой последовательности, а затем объединим эти результаты для получения ДПФ для всей последовательности.
Если на объединение результатов будет потрачено небольшое количество операций, то можно получить существенный выигрыш во времени.
N −1
Пусть: X p (k ) = ∑ x(n ) WNn k , k = 0, 1, ... , N −1. (1.4.1) n =0
Разделяя x(n ) на чётные и нечётные точки, получим:
|
|
|
|
|
|
- 43 - |
|
|
|
|
|
|
|
||
|
|
|
N −1 |
N −1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
X p (k ) = |
∑ x (n ) WNn k |
+ ∑ x (n ) WNn k . |
|
|
(1.4.2) |
||||||||||
|
|
|
n =0 |
n =0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
n − чётное |
n − нечётное |
|
|
|
|
||||||
|
Заменим индексы суммирования на n = 2 r |
при чётном n и |
|||||||||||||
n = 2 r +1 при нечётном n, получим: |
|
|
|
|
|
|
|||||||||
|
|
|
|
N |
−1 |
|
N |
−1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
X p (k ) |
= ∑ x(2 r ) WN2 r k + |
∑ x(2 r +1) WN(2 r +1) k . |
(1.4.3) |
||||||||||||
|
|
|
|
r =0 |
|
r =0 |
|
|
|
|
|
|
|
||
Поворачивающие множители WN(2 r +1)k =WNk WN2 r k , |
|
||||||||||||||
|
|
|
|
2 π |
|
|
|
− |
j |
2 π |
2 r k − j |
2 π |
r k |
|
|
n k |
|
|
2 r k |
|
|
|
r k |
||||||||
= e |
− j N n k |
= e |
|
N |
|
N /2 |
|||||||||
WN |
|
|
|
и |
WN |
|
|
|
= e |
|
|
=WN /2 |
|||
Тогда (6.4.3) можно переписать: |
|
|
|
|
|
|
|
|
|
||||||
|
|
N −1 |
|
N −1 |
|
|
|
|
|
|
|||||
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
||
X p (k )= |
∑ x(2 r ) WNr k/2 +WNk |
∑ x(2 r +1) WNr k/2 . |
(1.4.4) |
||||||||||||
|
|
r =0 |
|
r =0 |
|
|
|
|
|
|
|||||
|
|
|
|
N −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
Обозначим: ∑ x(2 r +1) WNr k/2 = F (k ) – ДПФ от последовательности |
|||||||||||||||
|
|
|
|
r =0 |
|
|
|
|
|
|
|
|
|
|
|
N −1 |
|
|
2 |
|
|
нечётных импульсов, а ∑ x(2 r ) WNr k/2 = G(k )– ДПФ от |
||
r =0 |
|
|
последовательности чётных импульсов. |
|
|
Тогда X p (k) = G(k) +WNk F(k). |
|
(1.4.5) |
Выражение (1.4.5) позволяет определить только первые N отсчёта. |
||
|
|
2 |
Так как X p (k ) должно быть определено для N точек k = 0, 1, 2, …, |
||
N–1, а G(k )и F (k ) определяются только для |
N |
точек k = 0, 1, 2, …, |
|
2 |
|
(N/2)–1, доопределим (1.4.5) для значений k = N/2, (N/2)+1, (N/2)+2, …, N–1.
Учитывая, что G(k )и F (k ) периодические функции с периодом
N |
|
|
|
N |
|
N |
k + |
N |
|
N |
|
||||
, то можно записать: |
|
2 |
, |
||||||||||||
X p |
+WN |
||||||||||||||
2 |
k + |
2 |
|
= G k + |
2 |
|
F k + |
2 |
|
||||||
(1.4.6) |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
- 44 - |
|
|
|
|
где |
|
N |
|
N |
= F (k ), |
(1.4.7) |
||
G k + |
2 |
|
= G(k ); F k + |
2 |
|
|||
|
|
|
|
|
|
|
||
а W k + |
N |
|
=W k e− j |
2 π |
N |
|
|
|
||||||
|
=W k W N / 2 |
|
|
|
=W k e− j π =W k (−1)= −W k . |
|||||||||
2 |
N |
2 |
||||||||||||
N |
|
N |
N |
|
N |
|
|
|
|
|
|
N |
N |
N |
|
|
X |
|
+ |
N |
|
|
|
|
|
|
|
|
|
Тогда |
|
k |
|
= G(k ) − W k |
F (k ) . |
(1.4.8) |
||||||||
|
|
p |
|
2 |
|
|
|
|
|
N |
||||
И окончательно |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
G(k ) |
+ WNk |
F (k ) |
, |
k = 0, 1, ... , N − 1 |
|
|||||||
X p (k ) |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
(1.4.9) |
= |
|
|
|
|
|
k = N , |
N |
|
||||||
|
|
G(k ) − WNk F (k ) |
, |
+ 1, ... ,N − 1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
Выражения (6.4.9) дают алгоритм вычисления ДПФ N-точечной |
||||||||||||||
последовательности через дискретное преобразование Фурье двух N/2-точечных последовательностей. Этот алгоритм можно
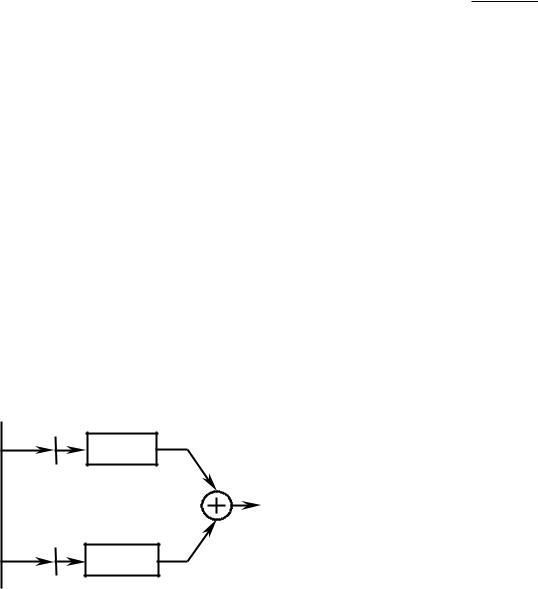
представить направленным графом, имеющим вид “бабочки” (рис.1.4.1):
G (k ) |
G(k ) +W k |
F (k ) = X |
p |
(k ) |
|
N |
|
|
F (k ) |
k |
k |
|
N |
|
WN |
G (k ) −WN |
F (k ) = X p k + |
2 |
|
|
|
|
|
|
|
|
Рис.1.4.1. Граф алгоритма БПФ с прореживанием по времени
Пояснения к рис.1.4.1.
- узел, линия выходит из узла вверх - суммирование , линия
выходит из узла вниз - вычитание ; стрелка – умножение на поворачивающий множитель.
Пример:
Построим алгоритм БПФ с прореживанием по времени для последовательности длиной N = 8 = 23 , т.е. для x(n ), где n = 0, 1, 2,
3, 4, 5, 6, 7. Разобьём исходную последовательность x(n) = x3 (n) на
две последовательности: |
x2,0 (n ) и |
x2,1 (n ), состоящие |
||
соответственно из чётных и нечётных членов x3 (n): |
||||
x 2 ,0 (n ) = {x (0 ), x (2 ), x (4 ), x (6 )}, |
(1.4.10) |
|||
x |
|
(n ) = {x (1), x |
(3 ), x (5 ), x (7 )}. |
|
2 ,1 |
|
|||
|
|
|
|
|
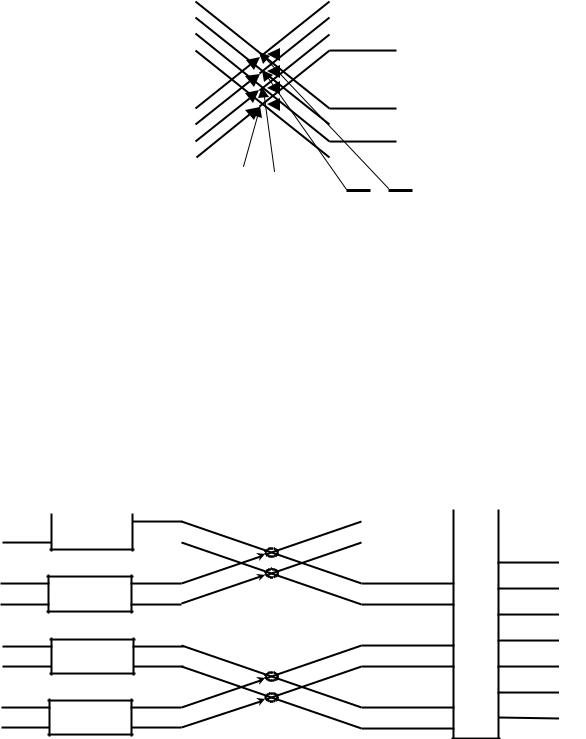
Граф алгоритма быстрого преобразования Фурье для этих последовательностей представлен на рис.1.4.2.
x(0)
x(2)
x(4)
x(8)
x(1)
x(3)
x(5)
x(7)
- 45 -
|
|
G0 |
|
|
|
|
|
|
|
X |
|
ДПФ N/2 |
G1 |
|
|
|
|
|
|
|
x(0) |
|
|
|
|
|
|
|
|
x(1) |
||
|
G2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x(2) |
||
|
|
G3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(3) |
|
|
|
F0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
x(4) |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
ДПФ N/2 |
F1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x(5) |
||
|
F2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x(6) |
||
|
|
F3 |
3 |
2 |
|
|
|
|
|
|
|
|
|
W8 |
W8 |
|
|
x(7) |
|||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
W 1 |
W 0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
8 |
8 |
|
Рис.1.4.2. Граф алгоритма БПФ для двух половинок последовательности x(n).
Теперь вновь разобьём последовательности (1.4.10) на последовательности из нечётных и чётных членов:
x1,0 (n ) = {x(0 ), x(4)},
(n ) = {x(2 ), x(6 )},
x2,2 (n ) = {x(1), x(5 )}, . (1.4.11)
x2,3 (n ) = {x(3), x(7 )},
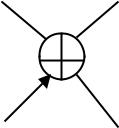
Последовательности (1.4.11) являются уже двухточечными. На рис. 1.4.3 приведен алгоритм БПФ последовательности длиной N=8.
x0 |
|
|
|
|
|
G0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ДПФ N=2 |
|
|
|
|
x(0) |
|||||
x4 |
G1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|||||
|
|
W 0 |
|
x(1) |
|
|
|
4 |
|
||
x2 |
1 |
G2 |
x(2) |
||
|
|
W4 |
|
||
x6 |
ДПФ N=2 |
G3 |
|
||
|
|
||||
|
|
|
|
x(3) |
|
x1 |
|
F0 |
АУ |
||
ДПФ N=2 |
x(4) |
||||
x5 |
F1 |
|
|||
0 |
x(5) |
||||
|
|
W4 |
|
|
|
x |
3 |
W40 |
F |
x(6) |
|
|
ДПФ N=2 |
2 |
x(7) |
||
x7 |
F3 |
||||
|
|
||||
Рис.1.4.3. Алгоритм БПФ последовательности длиной N=8.
Таким образом мы дошли до дискретного преобразования Фурье последовательности длиной N=2.
Для этой последовательности
- 46 -
N −1 |
|
|
|
1 |
|
Y (k) = ∑ y p (n) WNn k = ∑ y p (n) W2n k = y p (0) 1+ y p (1) W2k . |
(1.4.12) |
||||
n=0 |
|
|
|
n=0 |
|
|
= e− j |
2π |
|
|
|
Так как W 1 |
|
1 |
= −1, то |
|
|
2 |
|
||||
2 |
|
|
|
|
|
|
Y (0) = y(0) + y(1), а Y (1) = y(0) − y(0). |
(1.4.13) |
|||
На рис.1.4.4 приведен граф дискретного преобразования Фурье от последовательности длиной N=2.
y(0) |
|
|
Y(0 |
|
|
|
|
|
|
y(1) |
|
W 0 |
= 1 |
Y(1) |
|
|
|||||
|
2 |
|
|
|
|
Рис.1.4.4. Граф дискретного преобразования Фурье от последовательности длиной N=2.
Таким образом в рассматриваемом примере при N=8 имеем 3
этапа разбиения ( log2 8 = 3). В общем случае число этапов log2 N . На
каждом этапе экономим N/2 комплексных умножений и N/2 сложений.
На объединение требуется N log2 N арифметических операций.
Общее количество операций существенно сократилось.
Однако мы не можем работать непосредственно с входной последовательностью, так как ее необходимо реорганизовать (для нашего примера в первом этапе на две последовательности x(0), x(2), x(4), x(6) и x(1), x(3), x(5), x(7) соответственно). Для этого используется двоично-инверсионная последовательность, приведенная в таблице 6.1.
|
|
|
Таблица 6.1. |
|
исходная |
двоично- |
|
||
|
|
инверсионная |
||
десятичная |
двоичная |
двоичная |
десятичная |
|
0 |
000 |
000 |
0 |
|
1 |
001 |
100 |
4 |
|
2 |
010 |
010 |
2 |
|
3 |
011 |
110 |
6 |
|
4 |
100 |
001 |
1 |
|
5 |
101 |
101 |
5 |
|
|
|
- 47 - |
|
6 |
110 |
011 |
3 |
7 |
111 |
111 |
7 |
Используя двоично-инверсионную последовательность можно легко формировать реорганизованные последовательности.
1.4.1. Применение метода БПФ для вычисления обратного ДПФ.
Пусть известно дискретное преобразования Фурье последовательности x(n)
|
|
N −1 |
|
|
|
X p (k ) = ∑ x(n) WNn k , k = 0,1,..., N −1. |
(1.4.14) |
|
|
n=0 |
|
Найдем с помощью быстрого преобразования Фурье |
|
||
последовательность x(n). |
|
||
|
1 |
N −1 |
|
x(n ) = |
∑ X p (k ) WN−n k n = 0,1,..., N −1. (1.4.15) |
|
|
N |
|
||
|
k =0 |
|
|
При сравнении (1.4.14) и (1.4.15) видно, что их отличии состоит только лишь в знаке степени поворачивающегося множителя. Однако
алгоритм БПФ построен только для положительных степеней WNk n .
Будем считать, что в общем случае последовательность x(n) и X p (k )
комплексные величины. А так как
(W −k n ) |
= W k n |
и |
(W k n ) |
= W −k n . |
(1.4.16) |
N |
N |
|
N |
N |
|
Поэтому с учетом последних соотношений можно в обратном дискретном преобразовании Фурье перейти к сумме, вид которой аналогичен виду суммы прямого ДПФ, т. е.
1 |
N −1 |
|
|
1 |
|
N −1 |
|
|
|
x (n)= |
|
∑ X p (k ) WN−n k = |
|
|
∑ X p (k ) (WN−n k ) |
(1.4.17) |
|||
|
N |
||||||||
N |
k =0 |
1 |
|
|
k =0 |
|
|
||
|
|
|
N −1 |
|
|
|
|
|
|
или |
x (n)= |
|
∑ X p (k ) WNnk . |
|
(1.4.18) |
||||
N |
|
||||||||
|
|
|
k =0 |
|
|
|
|
|
|
Исходя из соотношений (1.4.17) и (1.4.18) решение выше |
|||||||||
названной задачи состоит из следующих этапов: |
|
|
|||||||
• по заданному ДПФ ( X p (k )) последовательности x(n) найти |
|||||||||
комплексно сопряженные X p (k);
• воспользовавшись алгоритмом БПФ для работы с
положительными |
|
степенями WNk n |
и вычислить |
||
~ |
N −1 |
|
nk |
|
|
|
|
; |
|
||
x |
(n) = ∑ X p |
(k ) WN |
|
||
|
k =0 |
~ |
|
|
|
|
~ |
|
|
|
|
• найти x (n) |
= [x |
(n)] ; |
|
||
- 48 - |
1 |
|
||
|
~ |
|||
• получить требуемое значение |
x(n) = |
|
x (n) . |
|
N |
||||
|
|
|
||
1.4.2. Применение БПФ для вычисления реакции
линейной дискретной цепи
Известно, что реакция y(n ) линейной дискретной цепи будет определяться в виде свёртки воздействия x(n ) и импульсной характеристики g(n ), т.е.
N −1
y(n ) = ∑ x(m) g(n −m) |
(6.4.19) |
, где |
|
m =0 |
|
N = N1 + N2 , N1 – длина воздействия, N 2 – длина импульсной
характеристики.
Свертку можно вычислить только для последовательностей одинаковой длины. Поэтому последовательности g(n) и x(n) дополняют справа нулями до длины N.
Так как Y p (k ) = X p (k ) H p (k ), то с помощью алгоритма быстрого преобразования Фурье вычислим X p (k ) и H p (k ), а затем
определяется y(n ).
Тогда алгоритм нахождения реакции ЛДС из следующих этапов:
|
|
N −1 |
|
||
• |
находим X p (k ) = ∑ x(n ) WNk n и |
|
|||
|
N −1 |
n =0 |
|
||
|
|
|
|
|
|
|
H p (k ) = ∑ h(n ) WNk n по алгоритму БПФ; |
|
|||
|
n =0 |
|
Y p (k ) = X p (k ) H p (k ); |
|
|
• |
находим |
|
|
||
• находим обратное преобразование Фурье по алгоритму БПФ |
|||||
|
|
1 |
|
N −1 |
|
|
y(n ) = |
|
|
∑ Y p (k ) WN−k n . |
|
|
N |
|
|
||
|
|
|
k =0 |
|
|
|
В действительности рассматриваемый |
случай является |
|||
исключительным, так как на практике чаще всего входная
последовательность x(n) бесконечная или очень большая. В свою очередь и импульсная характеристика h(n ) может быть как конечной,
так и бесконечной. В этом случае используется метод секционирования последовательности.
Рассмотрим метод секционирования на примере КИХ цепи.
Дляэтой цепи импульснаяхарактеристика конечнаисоставляетдлинуN.

|
|
|
|
|
|
|
- 49 - |
x(n) |
|
|
|
||
|
Исходная |
последовательность |
разбивается |
на |
|||||||||
последовательности |
x1(n ), x2 (n ), x3 (n ) ... |
|
причём |
эти |
|||||||||
последовательности выбираются с перекрытием. |
|
|
|
||||||||||
|
|
|
|
|
x(n) |
|
|
Длина последовательностей xi (n) |
|||||
|
x1(n) |
|
|
|
|
|
|||||||
|
|
x2(n) |
|
|
|
выбирается равной |
N 2 , причём |
||||||
|
|
|
|||||||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
N2 ≥ N , тогда длина свёртки будет |
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x3(n) |
|
|
определяться как |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
N1 |
= N2 + N |
−1 |
Для каждой последовательности xi (n) вычисляется свёртка, а так
как система линейная, то свёртки всех последовательностей суммируются. Так как имеются перекрытия секций и образуются дополнительные хвосты от перекрытий, то их надо отбросить.
Для последовательности xi (n) вычисляется свертка
~ |
N1 −1 |
yi |
(n) = ∑xi (m) h(n − m). |
|
m=0 |
Вполученной последовательности ~yi (n) отбрасываем
последние N −1 отсчетов, которые неверны |
из-за цикличности |
|
свертки. В итоге получаем: |
|
|
~ |
n = 0, 1, 2, ... , |
N 2 . |
yi (n)= yi (n) , где |
||
Результирующая последовательность y(n) представляется
путём последовательной подстыковки к значениям предыдущей свёртки с номером xi −1(n).
1.5.Цифровые фильтры и их синтез
Вобщем случае под цифровым фильтром понимается любой алгоритм обработки цифровых сигналов. Однако в данном разделе под цифровым фильтром будем понимать частотно-избирательные дискретные цепи.
Синтез фильтров состоит из следующих этапов:
1. Задания требований к фильтру
−требования к АЧХ или к характеристике ослабления,
−требования к ФЧХ,
−определение класса фильтра (рекурсивный или нерекурсивный).
2.Расчёт коэффициентов передаточной функции (по справочнику или аналитически).
3.Контроль выполнения требований и расчёт коэффициентов масштабирования, например, в рекурсивном фильтре может получиться коэффициент больше единицы, что может привести к потере устойчивости фильтра, следовательно, надо
- 50 -
уменьшить этот коэффициент в некоторое число раз – это и будет коэффициент масштабирования.
4. Выбор числа звеньев фильтра (фильтр может быть составлен из последовательно соединённых простейших ЛДС, рассмотренных ранее).
5.Реализация фильтра с соответствующей отладкой на основе программных и аппаратных средств отладки.
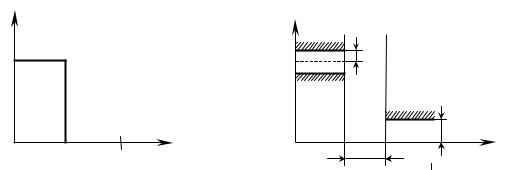
Рассмотрим задание требований к фильтру на примере цифрового фильтра нижних частот. Идеальная амплитудно-частотная характеристика этого фильтра приведена на рис.1.5.1. Исходные данные при проектировании фильтра следующие:
•полоса пропускания,
•величина отклонения АЧХ реального фильтра от АЧХ идеального фильтра в полосе пропускания,
•полоса заграждения,
•величина отклонения АЧХ реального фильтра от 0 в полосе заграждения,
•переходная полоса от полосы пропускания к полосе заграждения (требования не предъявляются),
•линейность ФЧХ.
T (ωˆ ) |
|
|
|
|
|
|
T (ωˆ ) |
|
|
1 |
|
1 |
1 |
|
|
|
|
||
|
|
ωˆ |
δ2 |
ωˆ |
ωˆ гр |
π |
ωП |
|
|
|
|
|||
0 |
|
0 |
π |
|
|
а) |
|
б) |
|
Рис.1.5.1. АЧХ идеального фильтра низких частот (а) и требования при его проектировании (б).
На рисунке введены следующие обозначения:
•± δ1 - максимальное отклонение от 1 нормированной
реальной АЧХ в полосе пропускания,
•δ21 - максимальное отклонение от 0 нормированной
реальной АЧХ в полосе заграждения,
•ωП - переходная полоса.
Нормированная амплитудно-частотная характеристика определяется в виде:
