11) ) Уравнение бегущей волны
Рассмотрим
колебания источника волны, происходящие
с циклической частотой ω 
и
амплитудойA:
где x(t) — смещение источника от положения равновесия.
В некоторую точку среды колебания придут не мгновенно, а через промежуток времени, определяемый скоростью волны и расстоянием от источника до точки наблюдения. Если скорость волны в данной среде равна υ, то зависимость от времени t координаты (смещение) x колеблющейся точки, находящейся на расстоянии r от источника, описывается уравнением
где k —волновое
число 
—
фаза волны.
Выражение (1) называется уравнением бегущей волны.
Бегущую волну можно наблюдать при следующем эксперименте: если один конец резинового шнура, лежащего на гладком горизонтальном столе, закрепить и, слегка натянув шнур рукой, привести его второй конец в колебательное движение в направлении, перпендикулярном шнуру, то по нему побежит волна.
12)
Декремент затухания. Добротность
ДЕКРЕМЕНТ
ЗАТУХАНИЯ (от лат.
decrementum - уменьшение, убыль) (логарифмический
декремент затухания) -
количественная характеристика быстроты
затухания колебаний в линейной системе;
представляет собой натуральный логарифм
отношения двух последующих максимальных
отклонений колеблющейся величины в
одну и ту же сторону. T. к. в линейной
системе колеблющаяся величина изменяется
по закону 
(где
постоянная величина
-
коэф. затухания) и два последующих наиб.
отклонения в одну сторону X1 и
X2 (условно
наз. "амплитудами" колебаний)
разделены промежутком времени
(условно
наз. "периодом" колебаний), то
,
а Д. з.
.
Так, напр., для механич. колебат. системы, состоящей из массы т, удерживаемой в положении равновесия пружиной с коэф. упругости k и испытывающей трение силой FT, пропорциональной скорости v (FТ =-bv, где b - коэф. пропорциональности), Д. з.
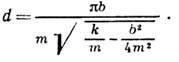
При
малом затухании 
.
Аналогично для электрич. контура,
состоящего изиндуктивности L,
активного сопротивления R и
ёмкости С,
Д. з.
.
При
малом затухании 
.
Для
нелинейных систем закон затухания
колебаний отличен от закона 
,
т. е. отношение двух последующих "амплитуд"
(и логарифм этого отношения) не остаётся
постоянным; поэтому Д. з. не имеет такого
определ. смысла, как для систем линейных.
13)
Уравнение Даламбера
