5) Применение теоремы о циркуляции вектора магнитной индукции. Магнитное поле внутри прямого проводника с током

В качестве примера применения теоремы о циркуляции вектора магнитной индукции для расчета индукции магнитного поля рассмотрим магнитное поле постоянного тока, текущего в бесконечно длинном прямом проводнике цилиндрической формы радиуса R. Замкнутый контур выберем в виде окружности радиуса r, лежащей в плоскости, перпендикулярной оси проводника, и с центром на этой оси (рис. 18).

Пусть направление обхода контура связано с направлением тока правилом правого винта. Из осевой симметрии следует, что во всех точках, равноудаленных от оси проводника с током, индукция магнитного поля одинакова. Проекция вектора магнитной индукции на направление элементарного перемещения совпадает по величине с магнитной индукцией во всех точках замкнутого контура.

Таким образом, для циркуляции вектора магнитной индукции получаем

, (1.12)

где – проекция вектора магнитной индукции на направление элементарного перемещения.

Если , то по закону полного тока:

. (1.13)

Из сравнения (1.12) и (1.13) следует

,

что совпадает с ранее полученной формулой (1.6).

Если , в предположении равномерного распределения тока по сечению проводника, по закону полного тока

, (1.14)

где – площадь, охватываемая контуром l; j – плотность тока. Из сравнения (1.12) и (1.14) следует

. (1.15)

На графике (рис. 19) показана зависимость индукции магнитного поля от расстояния до оси прямого проводника с током.

Рассмотрим полый проводник цилиндрической формы в виде трубы, вдоль стенки которой течет постоянный ток. Пусть R – радиус трубы. Замкнутый контур выберем также в форме окружности радиуса r с центром на оси проводника. Пусть . В этом случае контур не охватывает ток и

. (1.16)

Из сравнения (1.12) и (1.16) следует, что магнитное поле внутри полого проводника с током отсутствует. На рис. 20 представлена зависимость величины индукции магнитного поля в некоторой точке от ее расстояния до оси прямого полого проводника с током.

6)

Закон Фарадея для самоиндукции

L = const, если магнитная проницаемость μ среды и геометрические размеры контура постоянны. Знак минус в законе Фарадея в соответствии с правилом Ленца означает, что наличие индуктивности L приводит к замедлению изменения тока I в контуре. • Если ток I возрастает, то dI / dt > 0 и, соответственно, E_S < 0, т.е. ток самоиндукции I_S направлен навстречу току I внешнего источника и замедляет его нарастание.

• Если ток I убывает, то dI / dt < 0 и, соответственно, E_S> 0, т.е. ток самоиндукции I_S имеет то же направление, что и убывающий ток I внешнего источника и замедляет его убывание.

• Если контур обладает определенной индуктивностью L, то любое изменение тока I тормозится тем сильнее, чем больше L контура, т.е. контур обладает электрической инертностью.

где

 — электродвижущая сила,

 — число витков,

 — магнитный поток через один виток,

 — потокосцепление катушки.

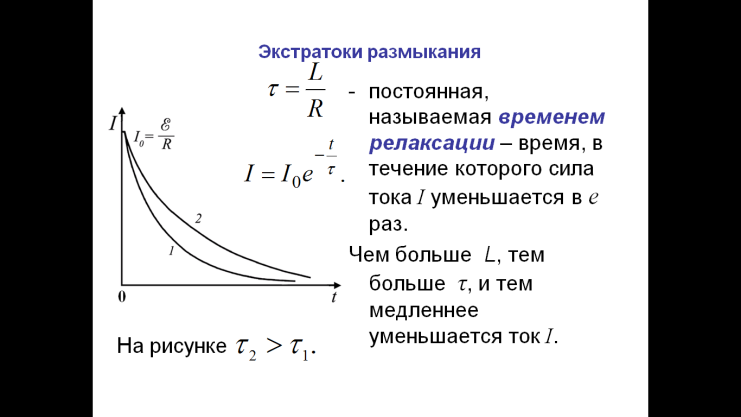
7)Экстратоки замыкания и размыкания

8) Уравнение Максвелла Максвелла уравнения в интегральной форме

Используя Гаусса- Остроградского формулу и С такса формулу, ур-ниям (1) - (4) можно придать форму интегральных:

Криволинейные интегралы в (1a),(2a) берутся по произвольному замкнутому контуру (их наз. циркуляция-ми векторных полей), а стоящие в правых частях поверхностные интегралы - по поверхностям, ограниченным этими контурами (опирающимся на них), причём направление циркуляции (направление элемента контура ) связано с направлением нормали кS (вектор ) правовинтовым соотношением (если в качестве исходного выбрано пространство с правыми системами координат). В интегралах по замкнутым поверхностям (S). в (3а), (4а) направление вектора элемента площади совпадает с наружной нормалью к поверхности;V- объём, ограниченный замкнутой поверхностью S.

M. у. в форме (1a) - (4a) предназначаются не только для изучения топологич. свойств эл.-магн. полей, но и являются удобным аппаратом решения конкретных задач электродинамики в системах с достаточно высокой симметрией или с априорно известными распределениями полей. Кроме того, в матем. отношении эта система ур-ний содержательнее системы (1) - (4), поскольку пригодна для описания разрывных, нодиффе-ренцируемых распределений полей. Но в отношении физ. пределов применимости обе системы ур-ний равнозначны, т. к. любые скачки полей в макроэлектродинамике должны рассматриваться как пределы микромасштабно плавных переходов, с тем чтобы внутри них сохранялась возможность усреднения ур-ний Лоренца - Максвелла. С этими оговорками резкие скачки можно описывать и в рамках M. у. (1) - (4), прибегая к аппарату обобщённых функций.

Наконец, M. у. в интегральной форме облегчают физ. интерпретацию MH. эл.-магн. явлений и поэтому нагляднее сопоставляются с теми экспериментально установленными законами, к-рым они обязаны своим происхождением. Так, ур-ние (1a) есть обобщение Био - Савара закона (с добавлением к току максвелловскогосмещения тока).

Ур-ние (2a) выражает закон индукции Фарадея; иногда его правую часть переобозначают через "магн. ток смещения"

где - плотность "магн. тока смещения", Ф_В - магн. поток. Ур-ние (За) связывают с именем Гаусса , установившим соленоидальность поляВ, обусловленную отсутствием истинных магн. зарядов. Впрочем вопрос о существовании магнитных монополейпока остаётся открытым. Но соответствующее обобщение M. у. произведено (Хевисайд, 1885) на основе принципа двойственной симметрии M. у. (см. в разделе 9), для чего в (2) и (2a) наряду с магн. током смещения вводится ещё и "истинный" магн. ток (процедура, обратная проделанной когда-то Максвеллом с электрич. током в первом ур-нии), а в ур-ние Гаусса (3), (За) - магн. заряд 

где - плотность магн. заряда. Фактически все экспериментальные установки для регистрации ожидаемых магнитных монополей основаны на этом предположении. Наконец, ур-ние (4a) определяет поле свободного электрич. заряда; его иногда называют законом Кулона (Ch. A. Coulomb), хотя, строго говоря, оно не содержит утверждения о силе взаимодействия между зарядами, да и к тому же справедливо не только в электростатике, но и для систем с произвольным изменением поля во времени. На тех же основаниях иногда и ур-нпе (Ia) связывают с именем Ампера (A. Ampere).