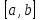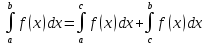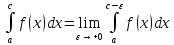shpory
.docx|
Предел функции
Предел –постоянное число а переменной х, при котором для каждого, наперед заданного произвольно малого положительного числа ε можно указать такое значение переменной х, что все последующие значения переменной будут удовлетворять |x-a|< ε. Предел
функции-Число
А
называется пределом функции
Предел на бесконечности Число
А
называется пределом функции
Односторонние пределы: бывают случаи, когда способ приближения аргумента х к а сущ-нно влияет на значение предела ф-ии. Поэтому вводится понятие одн. пределов. Односторонние
пределы: Если
в определении предела вместо условия
|x-a|<δ,
x≠a
наложить условие a<x<a+δ,то
мы получим односторонний предел
Если
a-δ<x<a,
то мы получим предел слева
Если предел слева и справа совпадают, то существует общий предел
|
Свойства пределов: (единственность и ограниченность). Теорема: Если предел существует, то он единственен. (Числовая последовательность может иметь только один предел.). Доказательство: метод от противного limx→af(x)=b, limx→af(x)=c, b/=c . Возьмем ε=∣b−c∣, по определению и свойству окрестности найдется выколотая окрестность т.а Uo(a,δ), в которой одновременно будут выполняться неравенства ∣f(x)−b∣<2∣b−c∣∣f(x)−c∣ <2∣b−c∣ ,тогда в точках этой же окрестности ∣b−c∣=∣(b−f(x))+(f(x)+c)∣≤ ∣f(x)−b∣+∣f(x)−c∣<2∣b−c∣+2∣b−c∣=∣b−c∣ противоречие (от неправильно допущения). Теорема: Ф-я ограничена в интервале, если для всех х из интервала |f(x)|<M<∞. Ф-я ограничена в точке х0, если она ограничена в некоторой(очень малой) окрестности этой точки. ● Если ф-я имеет limx→х0f(x)=b, то она ограничена в этой точке.
● Если ф-я б.б. в точке х0, то она не ограничена. P.S. Не всякая б.б. ф-я является ограниченной. P.P.S. Бесконечно большая ф-я(б.б.)-ф-я y=f(x) называется б.б. при x→х0, если для любого числа M>0 существует такое число δ= δ(М)>0, что для всех х, удовлетворяющих неравенству 0<|x-x0|< δ, выполняется неравенство |f(x)|>M. ● функция может быть неограниченна, но не быть бесконечно большой. Если
|
Бесконечно малые(определение). Б.м. величина-переменная, предел которой =0. (Ф-я y=f(x) называется б.м. при x→х0, если limx→х0f(x)=0.) Связь б.м. и б.б. величин.: Если
Свойства бесконечно малых:
Функция
называется ограниченной
в точке
(
|
Свойства пределов:
Если
Доказательство:
Если
Доказательство:
Если
Доказательство:
|
|
|
|||||||||||||||||
|
Предел монотонной ф-ии:
Если
ф-я f(x)
монотонна и ограничена при x<
x0
или
x>
х0,
то существует соответственно ее левый
предел
Следствие: ограниченная монотонная последовательность имеет предел.
Теорема
о пределе монотонной переменной:
монотонная
переменная всегда имеет предел, причем
если она возрастает и ограничена
сверху, она имеет предел конечное
число, а если она не ограничена, то
предел =
Если
она убывает и ограничена снизу, то она
имеет предел конечное число, а если
она не ограничена, то предел = Теорема (Вейерштрасса о пределе монотонной функции). Для того чтобы возрастающая на множестве E функция f : E → R имела левый предел при x → b − 0, x ∈ E, необходимо и достаточно, чтобы она была ограничена сверху, а для того чтобы она имела правый предел при x → a + 0, x ∈ E, необходимо и достаточно, чтобы она была ограничена снизу.
Эквивалентные БМФ
При вычислении предела произведения и частного бесконечно малые можно заменять на эквивалентные
Доказательство:
Замечание: В сумме или разности заменять бесконечно малые на эквивалентные вообще говоря нельзя |
Теорема о 2ух милиционерах(о сжатой переменной). Теорема называется так благодаря таким фактам. Если два милицейских удерживают между собой злоумышленника и при том направляются в клетку, то узник также должен идти туда. В различных странах эта теорема именуется по различному. Теорема сжатия, теорема о сэндвиче (или правило сэндвича), теорема о двух карабинерах, теорема о двух жандармах, теорема о трёх струнах, теорема о двух городовых. |
Основные пределы анализа (Замечательные пределы) Доказательство:
Теорема о сжатой переменной Если
при
случай
При
Тогда
Если
Если
Доказательство:
Доказательство:
1 Следствие:
Доказательство:
|
Непрерывные функции* Пусть точка x0 является внутренней точкой области определения функции y=f(x) Функция f(x) называется непрерывной в точке x0, если: 1.
она определена в х0 и в ее окрестности
существует f(x)<
Все элементарные функции непрерывны во внутренних точках области определения Элементарные функции:
f(x)
называется непрерывной на промежутке
Теорема: для того, чтобы ф-я определенная в х0 была непрерывна, необходимо и достаточно, чтобы б.м. приращению аргумента соответствовало б.м. приращение ф-ии.
Классификация точек разрыва Точки, в которых функция является не непрерывной, называются точками разрыва (подразумевается, что функция определена в окрестности точки разрыва)
В это случае точка x0 называется точкой устранимого разрыва
Точка x0 называется точкой скачка функции f(x), если в этой точке пределы слева и справа существуют, но не равны между собой
Устранимые разрывы и скачки называются разрывами первого рода
Бесконечные и неустранимые разрывы называются разрывами второго рода. |
|||||||||||||||||||
|
Теорема о непрерывных ф-ях. 1. Сумма, произведение и частное 2ух непрерывных ф-й – есть ф-я непрерывная( для частного за исключением тех значений аргумента, в которых делитель=0.) 2. Пусть ф-я u=g(x) непрерывна в точке х0,a ф-я y=f(u) непрерывна в u0=g0(x0). Тогда сложная ф-я f(g(x)), состоящая из непрерывных ф-й, непрерывна в х0. 3.Если ф-я y=f(x) непрерывна и строго монотонна на [a;b] оси Ох, то обратная ф-я y=g(x) также непрерывна и монотонна на соответствующем отрезке [c;d] оси Оу. Т.Вейерштрасса: Если ф-я непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений. Т.Коши:Если ф-я y=f(x) непрерывна на отрезке [a;b] и принимает на его концах неравные значения А и В, то на этом отрезке она принимает и все промежуточные значения между A и В. Теорема:Любая элементарная ф-я непрерывна всюду, где определена.
Производная* Производной
функцией
Функция должна быть определена в самой точке a и в ее окрестности Геометрический смысл производной В
пределе секущая становится касательной
к графику функции. Касательная – это
предельное положение соответствующей
секущей. При малых
Геометрический смысл производной состоит в том, что она совпадает с tg угла наклона касательной к графику функции в точке x0 Производная отвечает за возрастание и убывание функции. Там, где производная положительна, функция возрастает (причем, тем быстрее, чем производная). Там, где производная отрицательна, функция убывает.
Свойства производных*
Доказательство:
Производная сложной функции Ф-я сложная, если над независимой переменной производятся не одна, а несколько операций. Теорема: Если ф-я u=g(x) имеет производную в точке х, а ф-я y=f(u) имеет производную в точке u=g(x), то сложная ф-я y=f(g(x)) имеет производную в точке х. При диф-ии сложной ф-ии диф-е начинают с внешней операции, рассматривая при этом аргумент как единое целое.
Производная обратной функции: Если ф-я y=f(x) строго монотонна на интервале [a;b] и имеет неравную нулю производную в произвольной точке этого интервала, то обратная ей ф-я x=g(y) также имеет производную в соответствующей точке. Производная обратной ф-ии= обратной величине производной данной ф-ии.
|
Дифференциал*
Дифференциалом
функции в точке
Дифференциал является функцией двух аргументов:
Диф. Является линейной ф-ей.
Свойства дифференциалов:
(
при
малых
3. Диф- линеен. 4.duv= udv+vdu 5. Диф. Суммы, произведения и частного определяется также, как и производные. 6. Диф. Сложной ф-ии равено произведению производной этой ф-ии по промежуточному аргументу на на диф. Этого промежуточного Аргумента.
Теорема Лагранжа (Формула конечных приращений)
Пусть
функция
Теорема
Лагранжа
Док-во(с лекции).
|
Правило Лопиталя
Правило
Лопиталя годится для раскрытия
неопределенности типа
Если
Замечание:
Экстрмум* Точка называется точкой экстремума функции, если:
Необходимое условие для наличия экстремума Необходимым условием для наличия экстремума функции одного аргумента является обращение в нуль (или разрыв) производной этой функции Если промежуток возрастания сменяется промежутком убывания, то точка экстремума называется максимумом (локальным) Если промежуток убывания сменяется промежутком возрастания, то точка экстремума называется минимумом(локальным) Замечание: Максимум и минимум не нужно путать с наибольшим и наименьшим значением функции на промежутке Острый экстремум – точка разрыва производной. К такому экстремуму нельзя построить касательную
Монотонные функции* Убывающие или возрастающие функции называются монотонными Функция
Функция
Теорема Лагранжа (достаточное условие монотонности функции) Если
для всех точек промежутка
Доказательство:
Зафиксируем
любые точки
Согласно
теореме Лагранжа:
По
условию на всем интервале
Тогда
Промежутки монотонности дифференцируемой функции
На
промежутках, где производная сохраняет
знак, функция является монотонной.
Таким образом, промежуток монотонного
возрастания может смениться промежутком
монотонного убывания только в тех
точках, где производная меняет знак
( Для того чтобы найти промежутки возрастания и убывания дифференцируемой функции необходимо:
|
Асимптоты.: Определение . Асимптотой
графика функции называется прямая, к
которой неограниченно приближается
график функции при Различают вертикальные и наклонные асимптоты (в частности, горизонтальные). Прямая х = а называется вертикальной асимптотой, если хотя бы один из односторонних пределов f (а + 0), f (а – 0) равен бесконечности или не существует, то есть в точке х = а функция терпит разрыв второго рода. Пример. Найти
вертикальные асимптоты функции Решение. Знаменатель
дроби равен нулю в точках х = –
1, х = +1.
Значит функция в этих точках не
определена. Классифицируем разрыв,
вычислив односторонние пределы. Эту
работу можно уменьшить, если учесть
чётность функции:
у(– х) = у(х)
(см. рис. 25). Исследуем только одну
из точек разрыва, например,
х = –
1:
Прямая у = b называется горизонтальной асимптотой, если
выполняется условие
То
есть разность a (х) между
ординатами точек кривой и асимптоты
при Теорема. Чтобы график функции имел наклонную асимптоту, необходимо и достаточно, чтобы имели место соотношения:
причём
при
Если
k = 0,
Первообразная
функция, неопределенный интеграл.*
Функция
Первообразная
для
Теорема (Структура множества всех первообразных)
Все
первообразные для заданной
Доказательство:
Пусть
Рассмотрим
ч.т.д
Множества
всех первообразных для заданной
Интегрирование – нахождение интеграла. Операция является обратной к дифференцированию, т.е. для того чтобы проверить правильно ли взят интеграл нужно продифференцировать ответ. Если интеграл взят правильно, то она совпадает с подинтегральнной функцией.
|
|||||||||||||||||||
|
Свойства неопределенного интеграла:
Интегрирование – линейная операция
Доказательство:
Замечание: Название формулы интегрирование по частям объясняется следующим образом:
По частям интегралы берут от следующих функций:
Этот метод совпадает с заменой переменной, но без введения новой буквы
Вычисление объемов (по площадям поперечных сечений) Дано тело
Будем считать, что части настолько мелкие, что в пределах каждого отрезка поперечное сечение мало меняет форму
Приближение тем лучше, чем меньше куски
…
Выражение,
стоящее под знаком предела, является
интегральной суммой для функции
Предел
интегральной суммы равен соответствующему
определенному интегралу
|
Определенный интеграл Площадь криволинейной трапеции
В пределе, когда полоски вырождаются в вертикальные отрезки и погрешность стремиться к нулю
Определение определенного интеграла
Дана
функция
Составим
сумму
Определенным
интегралом от функции
Геометрический смысл определенного интеграла
Таким образом, геометрический смысл определенного интеграла состоит в том, что он для положительной функции совпадает с площадью соответствующей криволинейной трапеции
Свойства определенного интеграла
Верно для любого числа слагаемых
Доказательство:
Частная производная*
Рассмотрим
функцию
Тогда мы получим функцию от одной переменной x. Производная этой функции по переменной x называется частной производной z по x
Геометрический смысл частных производных
Частная
производная отвечает за возрастание
и убывание функции
|
Теорема о среднем значении
На
промежутке
Доказательство:
По одной из теорем о значении непрерывности функции, они заполняют весь промежуток между наименьшим и наибольшим значением
Формула Ньютона-Лейбница*
Замечание:
Известно,
что
Доказательство:
Мы
доказали, что интеграл с переменным
верхним пределом является первообразной
для подинтегральной функции.
Пусть
|
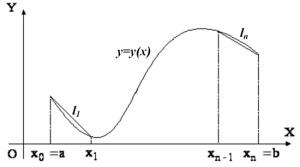
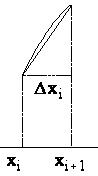
Длина
дуги кривой
На каждом из кусков заменим кривую на
прямую
Вычислим
длину каждого:
Будет
точным равенством, если
Выражение,
стоящее под знаком предела является
интегральной суммой для функции
Предел
интегральной суммы равен соответствующему
определенному интегралу
Несобственный интеграл При определении интеграла мы считаем, что подинтегральная функция непрерывна и промежуток интегрирования конечен. Если одно или оба из этих условий нарушаются, то интеграл называется несобственным Определенный интеграл по бесконечному промежутку Предположим,
что
Такой предел не обязан существовать. Если он существует, то интеграл называется сходящимся; если конечного предела не существует, то говорят, что интеграл расходится Предел не обязательно существует. Если предел существует, то интеграл сходящийся, в противном случае расходящийся интеграл сходящийся, если сходятся оба интеграла правой части Замечание: Интегралы, стоящие справа, нужно исследовать на сходимость по отдельности Интегралы от разрывных функций
Если этот предел существует, то интеграл называется сходящимся, в противном случае говорят, что интеграл расходится
Предел не обязательно существует
|
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||

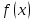 определена
в открытом интервале
определена
в открытом интервале
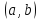 ,
содержащем точку
,
содержащем точку
 ,
за исключением может быть самой точки
,
за исключением может быть самой точки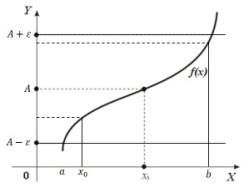
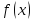 в
точке x0
(или при x–>x0)
если для любого ε>0
найдется δ>0,
такое что для всех x,
удовлетворяющих условию |x-x0|<δ,
x≠x0
справедливо неравенство |f(x)-A|<ε.
в
точке x0
(или при x–>x0)
если для любого ε>0
найдется δ>0,
такое что для всех x,
удовлетворяющих условию |x-x0|<δ,
x≠x0
справедливо неравенство |f(x)-A|<ε. при
x–>∞
если для любого положительного ε
(ε>0)
найдется δ>0,
такое что для всех x,
удовлетворяющих условию |x|>δ,
справедливо неравенство |f(x)-A|<ε
при
x–>∞
если для любого положительного ε
(ε>0)
найдется δ>0,
такое что для всех x,
удовлетворяющих условию |x|>δ,
справедливо неравенство |f(x)-A|<ε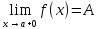

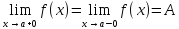 =>
=>
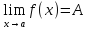
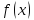 при
при
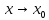 является
бесконечно большой (
является
бесконечно большой (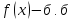 )
и
)
и ,
то
,
то
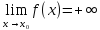
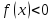 ,
то
,
то
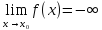
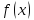 при
при
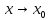 является
бесконечно большой (
является
бесконечно большой ( ),
то
),
то
 (и наоборот).
(и наоборот).
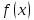 – бесконечно
малая
– бесконечно
малая
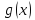 – бесконечно
малая
– бесконечно
малая

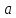 на некотором промежутке
на некотором промежутке
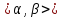 ,
если для любого из этого промежутка
выполняется неравенство
,
если для любого из этого промежутка
выполняется неравенство
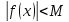 ,
где
,
где
 – какое-то фиксированное число. Пример:
– какое-то фиксированное число. Пример:
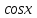 (ограничена на любом промежутке, т.к.
(ограничена на любом промежутке, т.к.
 )
)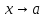
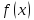 – бесконечно
малая
– бесконечно
малая
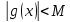
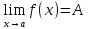

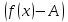 – бесконечно
малая равносильны
– бесконечно
малая равносильны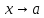 )
)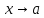
 – бесконечно
малая
– бесконечно
малая
 – бесконечно
малая
– бесконечно
малая
 ограничена
в районе точки
ограничена
в районе точки

 – бесконечно
малая
– бесконечно
малая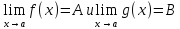 ,
то
,
то

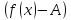 – б.м.
– б.м.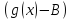 – б.м.
– б.м. – сумма
бесконечно малых бесконечно малая
– сумма
бесконечно малых бесконечно малая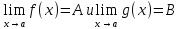 ,
то
,
то
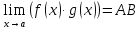
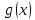 ,
имеющая предел в точке
,
имеющая предел в точке
 ,
ограничена в окрестности этой точки
,
ограничена в окрестности этой точки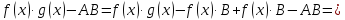
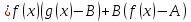
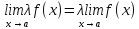

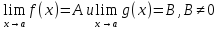 ,
то
,
то

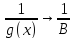 – ?
– ?
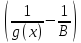 – б.м?
– б.м?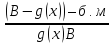
 – ограничена
при
– ограничена
при

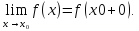
 .
.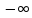 .
. Бесконечно
малые функции
Бесконечно
малые функции
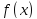 и
и
 называются
эквивалентными, если при
называются
эквивалентными, если при
 ,
,
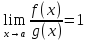
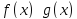








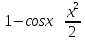
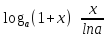
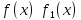
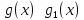
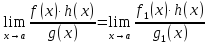
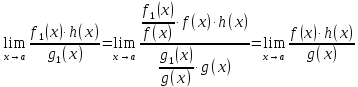
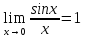
 ,
,
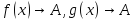 и
и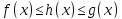 ,
тогда
,
тогда
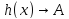
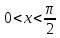 .
Рассмотрим единичную окружность
.
Рассмотрим единичную окружность

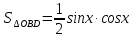
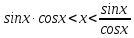
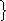

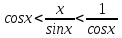
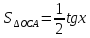


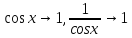
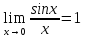
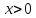 ,
то
,
то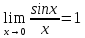
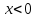 ,
то
,
то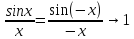

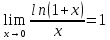

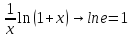
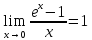
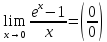

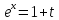





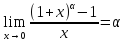 ,
,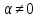
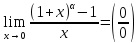
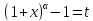


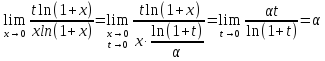
 .
.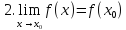
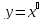
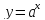

 ,
если она непрерывна во всех точках
этого промежутка.
,
если она непрерывна во всех точках
этого промежутка.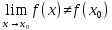 предел
существует, но функция в точке x0
не определена
предел
существует, но функция в точке x0
не определена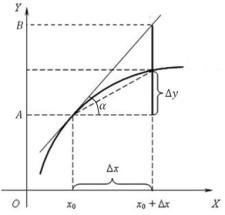


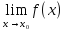 не
существует ни в конечном, ни в
бесконечном виде
не
существует ни в конечном, ни в
бесконечном виде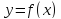 в
точке
в
точке
 называется
называется
 (основное понятие дифференциального
исчисления, хар-ее скорость изменения
ф-ии в данной точке)
(основное понятие дифференциального
исчисления, хар-ее скорость изменения
ф-ии в данной точке) секущая идет практически по графику
функции.
секущая идет практически по графику
функции. 




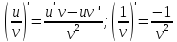
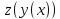 сложная
функция
сложная
функция
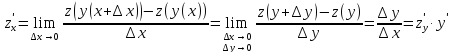
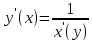


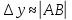
 -
дифференциал
функции y
-
дифференциал
функции y
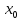 называется главная часть ее приращения,
равная произведению производной ф-ии
на приращение аргумента .
называется главная часть ее приращения,
равная произведению производной ф-ии
на приращение аргумента .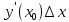
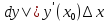
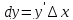
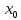 и
и
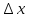
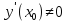 )
)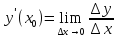
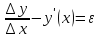 – б.м.
– б.м.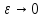
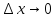
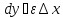
 :
:
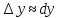
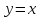 ,
то
,
то

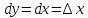

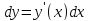
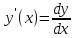
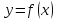 непрерывна
и дифференцируема на промежутке
непрерывна
и дифференцируема на промежутке
 ,
тогда внутри промежутка найдется
точка c,
такая что:
,
тогда внутри промежутка найдется
точка c,
такая что:
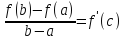

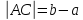
 утверждает,
что на кривой
утверждает,
что на кривой
 найдется
такая точка с,
в которой касательная параллельна
хорде AB
найдется
такая точка с,
в которой касательная параллельна
хорде AB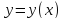

 – формула
конечных приращений
– формула
конечных приращений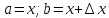

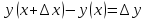
 ,
косвенно и для других видов
,
косвенно и для других видов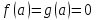 ,
то
,
то
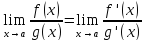

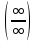
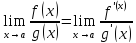
 и
и
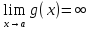
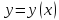 называется монотонно возрастающей
на промежутке
называется монотонно возрастающей
на промежутке
 ,
если для любых
,
если для любых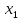 и
и
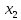 выполняется
неравенство
выполняется
неравенство
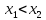
 строго
возрастающая
строго
возрастающая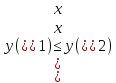 нестрого
возрастающая
нестрого
возрастающая называется монотонно убывающей на
этом промежутке, если
называется монотонно убывающей на
этом промежутке, если
 (строго
убывающая)
(строго
убывающая)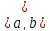
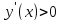 ,
то функция
,
то функция
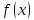 возрастает
возрастает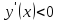 ,
то функция
,
то функция
 убывает
убывает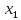 и
и
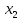 на
интервале, такие что
на
интервале, такие что
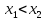
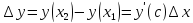 ,
где
,
где
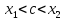
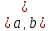
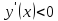 .
Следовательно,
.
Следовательно,

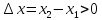 ,
т.к.
,
т.к.

 =>
=>
 => функция
=> функция
 убывает
убывает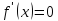 или не существует)
или не существует)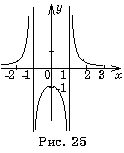
 называется
первообразной для
называется
первообразной для
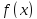 ,
если
,
если

 определена
неоднозначно. Если
определена
неоднозначно. Если
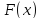 является первообразной, то первообразной
будут и все функции вида
является первообразной, то первообразной
будут и все функции вида
 (
( – произвольная постоянная)
– произвольная постоянная)
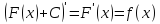
 имеют вид
имеют вид
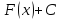 ,
где
,
где
 – любая первообразная,
– любая первообразная,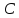 – произвольная постоянная
– произвольная постоянная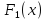 ,
,
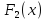 –
первообразные для
–
первообразные для
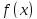 .
Покажем, что их разность является
постоянной величиной:
.
Покажем, что их разность является
постоянной величиной: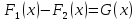
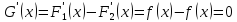
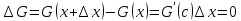
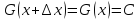
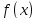 называются неопределенным интегралом
от
называются неопределенным интегралом
от
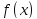
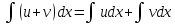



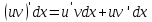
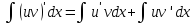
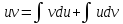
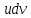
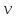 :
:
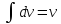
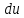 ,
ищем интеграл
,
ищем интеграл



 где
где
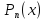 – многочлен в степени
– многочлен в степени
 ,
,
 .
.
 Интегрировать
нужно
Интегрировать
нужно
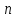 раз
раз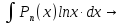
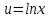
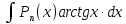
 За
За
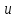 выбираются обратные тригонометрические
выбираются обратные тригонометрические
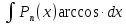 функции
функции
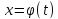
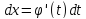
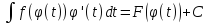
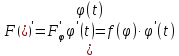
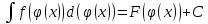
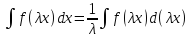
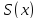 – площадь
поперечного сечения в точке
– площадь
поперечного сечения в точке

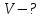
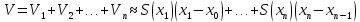
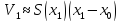 ,
где
,
где
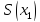 –
площадь основания,
–
площадь основания,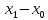 –
высота цилиндра
–
высота цилиндра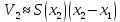


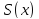 на промежутке
на промежутке

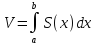
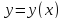 непрерывна
на промежутке
непрерывна
на промежутке
 ,
,
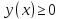
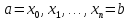

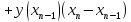
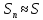 это
приближение будет тем точнее, чем уже
полоски и чем больше
это
приближение будет тем точнее, чем уже
полоски и чем больше
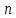

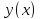 на промежутке
на промежутке
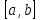 .
Разобьем промежуток
.
Разобьем промежуток
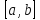 на
на
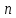 частей
точками
частей
точками
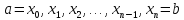
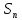 по
формуле
по
формуле

 называется
интегральной суммой для функции
называется
интегральной суммой для функции
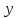 на промежутке
на промежутке
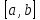 .
.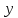 на промежутке
на промежутке
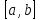 называется предел
называется предел
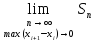
 .
Тогда
.
Тогда
 совпадает с площадью заштрихованной
ступенчатой фигур.
совпадает с площадью заштрихованной
ступенчатой фигур.

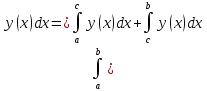


 ,
то
,
то
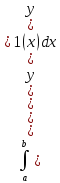
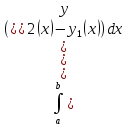 ,
т.к.
,
т.к.

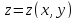 .
Зафиксируем
переменную y:
.
Зафиксируем
переменную y:
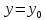
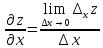 ;
;


 в направлении переменной
в направлении переменной
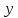 (т.е. когда
(т.е. когда
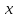 фиксирована). Точно также
фиксирована). Точно также
 отвечает за возрастание и убывание
функции
отвечает за возрастание и убывание
функции
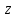 в направлении переменной
в направлении переменной
 (т.е. когда
(т.е. когда
 фиксирована).
фиксирована).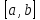 найдется точка
найдется точка
 ,
такая что
,
такая что


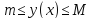 ,
,
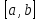

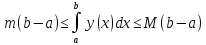

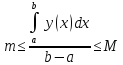
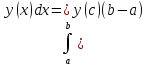
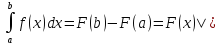
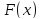 определяется
по
определяется
по
 неоднозначно,
но они все имеют вид
неоднозначно,
но они все имеют вид
 и при двойной подстановке постоянная
и при двойной подстановке постоянная
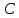 сокращается, т.е. правая часть формулы
Ньютона-Лейбница не зависит от выбора
первообразной
сокращается, т.е. правая часть формулы
Ньютона-Лейбница не зависит от выбора
первообразной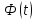
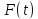 – другая первообразная. Любые две
первообразные отличаются на постоянную
– другая первообразная. Любые две
первообразные отличаются на постоянную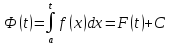
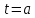
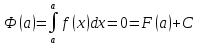

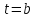
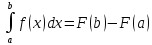

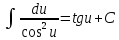

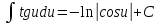
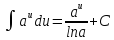
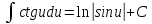

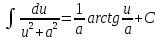
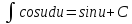
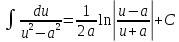
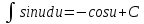
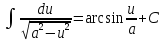
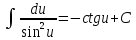
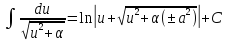



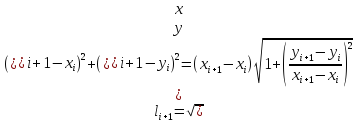


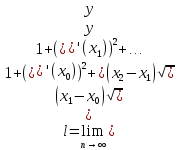

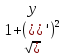 на
промежутке
на
промежутке
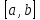
 – формула длины дуги
– формула длины дуги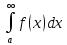


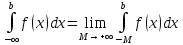
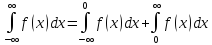
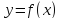 функция
имеет разрыв на промежутке
функция
имеет разрыв на промежутке