
Колледж телекоммуникаций DTO_Zanyatie_53
.docxМатематика 1 курс СПб ГУТ Колледж телекоммуникаций
ДТО
Занятие №
53 Геометрические преобразования
пространства
Занятие № 53 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ПРОСТРАНСТВА
-
Параллельный перенос.
-
Симметрия относительно плоскости.
-
Решение задач.
Определение. Движением пространства называется такое его преобразование, при котором сохраняются расстояния между точками.
-
Параллельный перенос.
Определение.
Параллельным переносом на вектор
 называется такое преобразование
пространства при котором любая точка
называется такое преобразование
пространства при котором любая точка
 переходит
в такую точку
переходит
в такую точку
 ,
что
,
что
 =
= .
.
Свойства параллельного переноса
-
Параллельный перенос есть движение;
-
При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя);
-
При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и тоже расстояние;
-
Каковы бы ни были точки Aи
 существует единственный параллельный
перенос при котором точка A
переходит в точку
существует единственный параллельный
перенос при котором точка A
переходит в точку
 ;
; -
Два параллельных переноса, выполненные последовательно дают параллельный перенос;
-
Преобразование обратное параллельному переносу есть параллельный перенос.
-
При параллельном переносе в пространстве каждая плоскость переходит в себя или в параллельную ей плоскость.
-
Параллельный перенос задаётся в пространстве формулами
 ,
,
 ,
,
 ,
выражающими координаты
,
выражающими координаты
 ,
,
 и
и
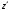 точки в которую переходит точка
точки в которую переходит точка
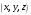 при параллельном переносе.
при параллельном переносе.
-
Симметрия относительно плоскости
Определение.
Симметрией относительно плоскости
 (зеркальной симметрией) называется
такое отображение пространства на себя
, при котором любая точка
(зеркальной симметрией) называется
такое отображение пространства на себя
, при котором любая точка
 переходит
в симметричную ей относительно плоскости
переходит
в симметричную ей относительно плоскости
 точку
точку
 .
.
Теорема. Зеркальная симметрия является движением.
Пример зеркальной симметрии.
На рисунке изображён план улицы зодчего Росси. Здания на противоположных сторонах улицы зеркально симметричны относительно вертикальной плоскости, идущей по оси симметрии её мостовой.

-
Решение задач.
Найдите
координаты точек, в которые переходят
точки
 ,
,
 и
и
 при зеркальной симметрии относительно
координатных плоскостей.
при зеркальной симметрии относительно
координатных плоскостей.
Решение.

Так
как у точки A координата
x равна нулю, то эта точка
лежит в плоскости YOZ. При
симметрии относительно плоскости YOZ
точка A переходит сама в
себя. При симметрии относительно
плоскости XOY точка
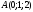 переходит
в точку
переходит
в точку
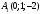 ,
а при симметрии относительно плоскости
XOZ - в точку
,
а при симметрии относительно плоскости
XOZ - в точку .
.
Остальные точки рассмотреть самостоятельно
Контрольные вопросы и задания:
-
Какая фигура не обладает осью симметрии
а) конус; в) наклонная призма;
б) цилиндр; г) куб;
-
Какая фигура является центрально симметричной
а) тетраэдр; в) конус;
б) усеченный конус; г) шар;
-
При центральной симметрии
1) прямая не проходящая через центр симметрии, отображается на:
а) параллельную ей прямой; в) пересекающую её прямую;
б) перпендикулярную ей прямую; г) что-то др.
2) прямая проходящая через центр симметрии, отображается на :
а) себя; в) перпендикулярную прямую;
б) параллельную прямую; г) луч;
-
Найдите координаты т.С, в которую переходит т.В (3; -1; 4) при
1) центральной симметрии относительно начало координат;
2) осевой симметрии относительно оси ОZ;
3) осевой симметрии относительно оси ОУ;
4) осевой симметрии относительно оси ОХ;
5) при зеркальной симметрии относительно плоскости ХОУ;
6) при зеркальной симметрии относительно плоскости ХОZ;
7) при зеркальной симметрии относительно плоскости YOZ.
