
- •Содержание
- •Динамика ввп рф в 2000-2011 гг.
- •Задание 3.
- •1.Для анализа ряда динамики определите: абсолютные приросты, темпы роста и прироста, среднегодовой темп роста и прирост. Прокомментируйте результаты.
- •2. Исследовать и охарактеризовать сезонные колебания объема реализации овощей магазинами города за 4 г., рассчитав индексы сезонности.
- •Список литературы
2. Исследовать и охарактеризовать сезонные колебания объема реализации овощей магазинами города за 4 г., рассчитав индексы сезонности.
|
Месяц |
Объем реализации, млн. руб. |
|||
|
1-й год |
2-й год |
3-й год |
6-й год |
|
|
Январь |
18,7 |
8,8 |
24,7 |
65,7 |
|
Февраль |
19,9 |
9,7 |
23,1 |
66,8 |
|
Март |
21,1 |
12 |
25,7 |
67,9 |
|
Апрель |
20,5 |
15,4 |
24 |
65,1 |
|
Май |
30,4 |
17,4 |
33,7 |
65,6 |
|
Июнь |
32,6 |
20,1 |
40 |
71,5 |
|
Июль |
34,7 |
25,7 |
43,4 |
78 |
|
Август |
41,2 |
28,6 |
49,7 |
82,5 |
|
Сентябрь |
45,8 |
30,1 |
53,3 |
87,7 |
|
Октябрь |
40,4 |
26,9 |
42,9 |
79,4 |
|
Ноябрь |
30,6 |
11,5 |
29,8 |
73,7 |
|
Декабрь |
21,5 |
12,3 |
25,6 |
61,3 |
Решение:
Определим индексы сезонности для каждого месяца:
 ,
где
,
где
 – значение среднего показателя по
месяцам;
– значение среднего показателя по
месяцам;
 – среднее значение за весь период.
– среднее значение за весь период.
Расчет представим в таблице.
|
Месяц |
Объем реализации, млн. руб. |
Итого |
|
|
|||
|
1-й год |
2-й год |
3-й год |
6-й год |
||||
|
Январь |
18,7 |
8,8 |
24,7 |
65,7 |
117,9 |
29,48 |
76,2 |
|
Февраль |
19,9 |
9,7 |
23,1 |
66,8 |
119,5 |
29,88 |
77,2 |
|
Март |
21,1 |
12 |
25,7 |
67,9 |
126,7 |
31,68 |
81,9 |
|
Апрель |
20,5 |
15,4 |
24 |
65,1 |
125 |
31,25 |
80,8 |
|
Май |
30,4 |
17,4 |
33,7 |
65,6 |
147,1 |
36,78 |
95,1 |
|
Июнь |
32,6 |
20,1 |
40 |
71,5 |
164,2 |
41,05 |
106,1 |
|
Июль |
34,7 |
25,7 |
43,4 |
78 |
181,8 |
45,45 |
117,5 |
|
Август |
41,2 |
28,6 |
49,7 |
82,5 |
202 |
50,50 |
130,5 |
|
Сентябрь |
45,8 |
30,1 |
53,3 |
87,7 |
216,9 |
54,23 |
140,2 |
|
Октябрь |
40,4 |
26,9 |
42,9 |
79,4 |
189,6 |
47,40 |
122,5 |
|
Ноябрь |
30,6 |
11,5 |
29,8 |
73,7 |
145,6 |
36,40 |
94,1 |
|
Декабрь |
21,5 |
12,3 |
25,6 |
61,3 |
120,7 |
30,18 |
78,0 |
|
Итого |
357,4 |
218,5 |
415,9 |
865,2 |
1857 |
|
100,0 |
Построим сезонную волну на графике.
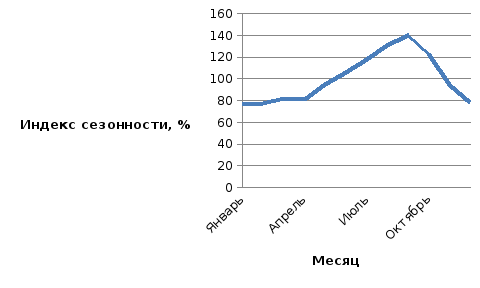
Таким образом, мы видим, что в летние месяцы наблюдается рост реализации, а в зимние его сокращение.
Задание 4. Сравните распределение денежных доходов населения России за 2006 и 2007 гг. с помощью коэффициента Джини, сделайте выводы.
|
Группы населения по доходам (20%-е группы) |
Доля в совокупных доходах, % |
|
|
2006 |
2007 |
|
|
Первая (с наименьшими доходами) |
4,2 |
5,5 |
|
Вторая |
16,4 |
18 |
|
Третья |
20,1 |
20,4 |
|
Четвертая |
25,7 |
9,1 |
|
Пятая (с наибольшими доходами) |
33,6 |
47 |
|
Итого |
100 |
100 |
Решение:
Коэффициент Джини (G) определим по формуле:
 ,
где
,
где
 - доля i-й
группы в общем объеме совокупности;
- доля i-й
группы в общем объеме совокупности;
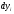 - доля i-й
группы в общем объеме изучаемого
признака;
- доля i-й
группы в общем объеме изучаемого
признака;
 - накопленная доля i-й
группы в общем объеме изучаемого
признака.
- накопленная доля i-й
группы в общем объеме изучаемого
признака.
Вспомогательные расчеты произведем в таблице.
|
Группы населения по доходам (20%-е группы) |
Доля в совокупных доходах, % |
|
|
|
|
|
|
2006 |
||||||
|
Первая (с наименьшими доходами) |
4,2 |
0,2 |
0,042 |
0,0084 |
0,042 |
0,0084 |
|
Вторая |
16,4 |
0,2 |
0,164 |
0,0328 |
0,206 |
0,0412 |
|
Третья |
20,1 |
0,2 |
0,201 |
0,0402 |
0,407 |
0,0814 |
|
Четвертая |
25,7 |
0,2 |
0,257 |
0,0514 |
0,664 |
0,1328 |
|
Пятая (с наибольшими доходами) |
33,6 |
0,2 |
0,336 |
0,0672 |
1 |
0,2 |
|
Итого |
100 |
1 |
1 |
0,2 |
- |
0,4638 |
Получаем
в 2006 году:
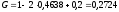 .
.
|
Группы населения по доходам (20%-е группы) |
Доля в совокупных доходах, % |
|
|
|
|
|
|
2007 |
||||||
|
Первая (с наименьшими доходами) |
5,5 |
0,2 |
0,055 |
0,011 |
0,055 |
0,011 |
|
Вторая |
18 |
0,2 |
0,18 |
0,036 |
0,235 |
0,047 |
|
Третья |
20,4 |
0,2 |
0,204 |
0,0408 |
0,439 |
0,0878 |
|
Четвертая |
9,1 |
0,2 |
0,091 |
0,0182 |
0,53 |
0,106 |
|
Пятая (с наибольшими доходами) |
47 |
0,2 |
0,47 |
0,094 |
1 |
0,2 |
|
Итого |
100 |
1 |
1 |
0,2 |
- |
0,4518 |
Получаем
в 2007 году:
 .
.
Так как, показатель Джини вырос с 0,2724 до 0,2964, то уровень концентрации (неравномерности) выше в 2007 году.
Задание 5. По данным о реализации молочной продукции на городском рынке рассчитать сводные индексы товарооборота, цен и физического объема реализации, а также абсолютное изменение этих показателей.
|
Продукт |
Товарооборот, млн. руб. |
Изменение цены в октябре по сравнению с августом, % |
|
|
август |
октябрь |
||
|
Молоко |
9,7 |
9 |
2,2 |
|
Сыр |
4,5 |
4,2 |
4 |
|
Творог |
14,5 |
14 |
3,1 |
|
Сметана |
20 |
18,4 |
2,5 |
Решение:
Сводный индекс товарооборота определим по формуле:
 ,
где
,
где
 - товарооборот в октябре;
- товарооборот в октябре;
 - товарооборот в августе.
- товарооборот в августе.
Получаем:
 .
.
Сводный индекс цен определим по формуле:
 ,
где
,
где
 - индивидуальный индекс цен, который
определим по формуле:
- индивидуальный индекс цен, который
определим по формуле:
 ,
где
,
где
 - изменение
цены в октябре по сравнению с августом.
- изменение
цены в октябре по сравнению с августом.
Получаем:
-
по молоку:
 ;
;
-
по сыру:
 ;
;
-
по творогу:
 ;
;
-
по сметане:
 .
.
Тогда:
 .
.
Сводный индекс физического объема определим по формуле:
 .
.
Проверка:
 .
.
Определим абсолютное изменение:
-
общее:
 млн.
руб.;
млн.
руб.;
- за счет изменения цен:
 млн.
руб.;
млн.
руб.;
- за счет изменения физического объема:
 млн.
руб.
млн.
руб.
Проверка:
 млн. руб.
млн. руб.
Таким образом, товарооборот сократился в 0,936 раза или на 3,1 млн. руб., в том числе за счет цен он вырос в 1,028 раза или на 1,23 млн. руб., а за счет изменения физического объема сократился в 0,911 раза или на 4,33 млн. руб.



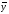 =38,69
=38,69








