37. Электрическое смещение. Теорема Гаусса для электростатического поля в диэлектрике.
Введём электрическое смещение – величину, не зависящую от свойств среды.
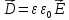
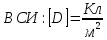
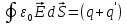Теорема
Гаусса для электростатического поля в
диэлектрике:
(3)
т.
е. поток вектора смещения электростатического
поля в диэлектрике сквозь любую замкнутую
поверхность равен алгебраической сумме
свободных электрических зарядов,
заключенных внутри этой поверхности.
В такой форме теорема Гаусса верна для
электростатического поля как для
однородной и изотропной, так и для
неоднородной и анизотропной сред.
Для
вакуума Dn =
ε0En (ε=1),
и поток вектора напряженности Е сквозь
произвольно выбранную замкнутую
поверхность равен
Так
как источниками поля Е в
среде являются как свободные, так и
связанные заряды, то теорему Гаусса для
поля Е в
самом общем виде можно записать
как
где
∑Qi и
∑Qsv—
соответственно алгебраические суммы
свободных и связанных зарядов, которые
охватываются замкнутой поверхностью
S. Но эта формула неприменима для описания
поля Е в
диэлектрике, поскольку она выражает
свойства неизвестного поля Е через
связанные заряды, которые, в свою очередь,
определяются им же. Это еще раз показывает
целесообразность введения вектора
электрического смещения.
38. Условия на границе раздела двух диэлектрических сред.
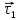
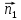
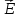(вектора напряжённости электрического
поля).
E1 E2
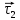
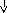
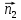
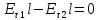
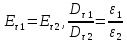
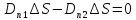
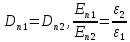
При переходе из первого диэлектрика во второй остаются равными: тангенциальная составляющая напряжённости и нормальная составляющая электрического смещения, изменяются нормальная составляющая напряжённости и тангенциальная составляющая электрического смещения. Силовые линии поля (напряжённости) преломляются при переходе из одного диэлектрика в другой и испытывают разрыв. Линии электрического смещения только преломляются, разрыва – нет.
39. Энергия системы зарядов.
Энергия системы зарядов.
1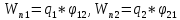
40. Энергия проводника, конденсатора.
1
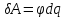
2
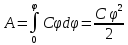
Энергия конденсатора.
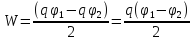
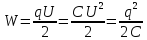
41. Энергия электрического поля. Объёмная плотность энергии.
В случае однородного поля.
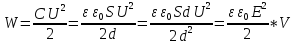
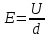
В случае неоднородного поля.
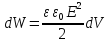
Энергия локализована (сосредоточена) в поле.
Объёмная плотность энергии электростатического поля – энергия единицы объёма.
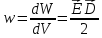
Эта (данная) формула справедлива в случае изотропного диэлектрика.
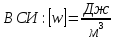
42. Характеристики электрического поля. Условия существования. Уравнение непрерывности.
Электрический ток – это упорядоченное движение электрических зарядов.
Условия существования:
наличие свободных заряженных частиц;
наличие электрического поля.
Сила тока – это величина, определяемая зарядом, проходящим через поперечное сечение проводника в единицу времени.
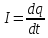
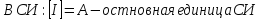
Плотность тока – это величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярно направлению тока.
Плотность тока – это вектор, направление которого совпадает с направлением упорядоченного движения положительно заряженных частиц.
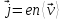
Определим плотность тока (покажем это выражение).
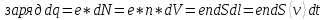
Сила тока сквозь произвольную поверхность S:
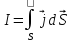
С учётом определения силы тока, а так же исходя из определения полного потока сквозь замкнутую поверхность, можно записать уравнение непрерывности (уравнение закона сохранения электрического заряда):
Убыль заряда в объёме в единицу времени равна полному потоку плотности тока через поверхность, охватывающую объём, в которой находится заряд.
В случае постоянного тока распределение заряда остаётся постоянным (распределение заряда постоянно).
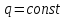
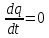
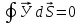
Уравнение непрерывности.
Дифференциальная форма общего уравнения непрерывности такова:
|
|
где
∇• — дивергенция,
t — время,
j — плотность потока (см. ниже),
σ — добавление q на единицу объёма в единицу времени. Члены, которые добавляют (σ > 0) или удаляют (σ < 0) q, называются «источниками» и «стоками» соответственно.
Это общее уравнение может быть использовано для вывода любого уравнения непрерывности, начиная с простого уравнения неразрывности и до уравнения Навье-Стокса.
Если q — сохраняющаяся величина, которая не может быть создана или уничтожена (например, энергия), тогда σ = 0, и уравнение непрерывности принимает вид:
