19. Свойства определенного интеграла

Пусть действительная функция f(x) определена и ограничена на отрезке [a, b]. Разобьем данный отрезок на n частичных интервалов. В каждом интервале выберем произвольную точку ξi и составиминтегральную сумму , где Δxi − длина i-го интервала. Определенным интегралом от функции f(x) на отрезке [a, b] называется предел интегральной суммы (суммы Римана) при стремлении максимальной длины частичного интервала к нулю. 

Определенный интеграл от единицы равен длине интервала интегрирования:

Постоянный множитель можно выносить за знак определенного интеграла:

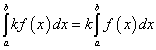
Определенный интеграл от суммы функций равен сумме интегралов от этих функций:

Определенный интеграл от разности функций равен разности интегралов от этих функций:

Если верхний предел равен нижнему, то определенный интеграл равен нулю:

При перестановке пределов интегрирования определенный интеграл изменяет знак на противоположный:

Пусть точка c принадлежит отрезку [a, b]. Тогда определенный интеграл от функции f(x) на отрезке[a, b] равен сумме интегралов на частичных промежутках [a, c] и [c, b]: 

Определенный интеграл от неотрицательной функции всегда больше или равен нулю:

Определенный интеграл от неположительной функции всегда меньше или равен нулю:

Формула Ньютона-Лейбница

Метод подстановки для определенного интеграла

Интегрирование по частям

Приближенное вычисление определенного интеграла по формуле трапеций 

Приближенное вычисление определенного интеграла по формуле Симпсона (метод парабол) 

Площадь криволинейной трапеции 

Площадь между двумя кривыми 

20. Формула Ньютона Лейбнеца

Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.

Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x) , вычислить ее значения в точках a и b и найти разность F(b) – F(a).

21. Интегрирование по частям в определенном интеграле

Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы

для определённого:

Предполагается, что нахождение интеграла  проще, чем . В противном случае применение метода неоправданно.

22. Определение и свойства двойного интеграла

1. Аддитивность. Если функция f(x, y) интегрируема в области D и если область D при помощи кривой Г площади нуль разбивается на две связные и не имеющие общих внутренних точек области D1 и D2, то функция f(x, y) интегрируема в каждой из областей D1 и D2, причем

2. Линейное свойство. Если функции f(x, y) и g(x, y) интегрируемы в области D, а α и β - любые вещественные числа, то функция [α · f(x, y) + β· g(x, y)] также интегрируема в области D, причем

3. Если функции f(x, y) и g(x, y) интегрируемы в области D, то и произведение этих функций интегрируемо в D.

     4. Если функции f(x, y) и g(x, y) обе интегрируемы в области D и всюду в этой области f(x, y) ≤ g(x, y), то

     5. Если функция f(x, y) интегрируема в области D, то и функция |f(x, y)| интегрируема в области D, причем

(Конечно, из интегрируемости |f(x, y)| в D не вытекает интегрируемость f(x, y) в D.)

     6. Теорема о среднем значении. Если обе функции f(x, y) и g(x, y) интегрируемы в области D, функция g(x, y) неотрицательна (неположительна) всюду в этой области, M и m - точная верхняя и точная нижняя грани функции f(x, y) в области D, то найдется число μ, удовлетворяющее неравенству m ≤ μ ≤ M и такое, что справедлива формула

     (11)

     В частности, если функция f(x, y) непрерывна в D, а область D связна, то в этой области найдется такая точка (ξ, η), что μ = f(ξ, η), и формула (11) принимает вид

     7. Важное геометрическое свойство.  равен площади области D