1. Предел функции.

Преде́л фу́нкции — одно из основных понятий математического анализа. Функция f(x) имеет предел A в точке x0, если для всех значений x, достаточно близких к x0, значение f(x) близко к A.

2. Бесконечно малые и бескончено большие функции

Функция y = f(x) называется бесконечно большой при x →x0, если для любого числа М > 0 существует число δ = δ(M) > 0, что для всех х, удовлетворяющих неравенству 0 < |x - x0|< δ, выполняется неравенство |f(x)| > М. Записывают или f(x) → ∞ при x →x0.

Функция y = f(x), заданная на всей числовой прямой, называется бесконечно большой при x → ∞, если для любого числа М > 0 найдется такое число N=N(M) > 0, что при всех x, удовлетворяющих неравенству |x| > N, выполняется неравенство | f(x)| > M.

3. Теоремы о пределе суммы, произведения и частного

Теоремы:

1)Предел суммы двух функций равен сумме их пределов:.

2)Предел произведения двух функций равен произведению их пределов:.

3)Предел частного двух функций равен пределу делимого, деленного на предел делителя, если предел делителя не равен:.

4. Первый замечательный предел

Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.

5. 2ой-4ый замечательный предел

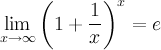
e – это иррациональное число: e≈2,7…

Нередко можно встретить модификацию второго замечательного предела:

Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к .

6. Непрерывность функции

Функция  называется непрерывной в точке , если:

• функция  определена в точке  и ее окрестности;

• существует конечный предел функции  в точке ;

• это предел равен значению функции в точке , т.е. 

определения:

Функция  непрерывна в точке , предельной для множества , если  имеет предел в точке , и этот предел совпадает со значением функции.

Функция непрерывна в точке, если её колебание в данной точке равно нулю.

7. Односторонние пределы

Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва).

Функция  называется непрерывной при  , если ее левосторонний и правосторонний пределы существуют, между собой равны и равны значению функции в этой точке, т.е. равны  .

8. Производная суммы частного и произведения определения

Производная суммы

Пусть  — две функции, определенные на одном и том же промежутке. Тогда производная суммы этих функций равна сумме их производных, если они существуют, т. е.

Производная произведения

Производная произведения двух функций и вычисляется по формуле

Производная частного

Если функции имеют в точке х производные и если то в этой точке существует производная их частного которая вычисляется по формуле

9. Дифференцирование сложной функции (теорма)

Теорема 1. Пусть функция z = f(x, y) дифференцируема в точке (x0, y0) и ее аргументы x = x(t) и y = y(t) дифференцируемы в точке t0 , причем x(t0) = x0 , y(t0) = y0 .

Тогда сложная функция z = f(x(t), y(t)) переменной t дифференцируема в точке t0 и ее производная вычисляется по формуле

Теорема 2. Пусть функция z = f(x, y) дифференцируема в точке (x0, y0) и ее аргументы x = x(u, v) и y = y(u, v) дифференцируемы в точке (u0, v0) , причем x(u0, v0) = x0 , y(u0, v0) = y0 .

Тогда сложная функция z = f(x(u, v), y(u, v)) переменных u и v дифференцируема в точке (u0, v0) и ее частные производные вычисляются по формулам

10. Таблица производных

Таблица производных, производные основных элементарных функций