33

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

Введение

Настоящее пособие предназначено для знакомства с основами линейной алгебры и содержит разделы, посвященные теории матриц и теории систем линейных уравнений. Оно предназначено студентам 1-го курса и может быть полезно всем, кого интересует простое и компактное изучение материала.

В каждом параграфе, кроме краткого изложения теории, содержатся примеры с решениями и упражнения для самостоятельного решения. Приведены также типовые индивидуальные задания.

Нумерация формул и рисунков в пособии сквозная. Ключевые слова в определениях и формулировках утверждений выделены курсивом.

С развитием компьютерной техники появилась возможность решать многие задачи линейной алгебры, не очень доступные в недалеком прошлом ввиду сложности вычислений. Как известно, для решения математических задач существует много различных программных пакетов. Универсальным пакетом является пакет MATHEMATICA. Примеры вычислений в пакетеMATHEMATICAв приложении. Освоив предложенные в пособии методы вручную, рекомендуем проделать вычисления с использованием компьютера.

Литература.

1. Курош А.Г. Курс высшей алгебры. – М.: Наука, 1977.

2. Фаддеев Д.К., Соминский И.С. Задачи по высшей алгебре. – СПб.: Издательство «Лань», 1998.

3. Краснов М.Л., Киселев А.И., Макаренко Г.И., Шикин Е.В., Заляпин В.И., Соболев С.К. Вся высшая математика: Учебник. Т. 1. – М.: Эдиториал УРСС, 2000.

4. Данко П.Е, Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. - М.: Высшая школа, 1999. Ч.1.- 304 с. - Ч.2. - 416 с.

5. Фридман Г. Н., Леора С.Н. Математика & Mathematica. Избранные задачи для избранных студентов. – Невский Диалект, БХВ-Петербург , 2010, 299 с.

1. Матрицы и действия с матрицами.

Матрицей размера называется прямоугольная таблица чисел, содержащаястрок истолбцов. Матрицы обозначают прописными (заглавными) буквами латинского алфавита. Числа, составляющие матрицу, называютсяэлементами матрицы¹ и обозначаются строчными буквами с двойным индексом: , где первый индекс () соответствует номеру строки, а второй индекс () – номеру столбца. Матрица размераможет быть записана в одном из видов

.

либо

При необходимости указать размер матрицы будем использовать запись .

Элементы матрицы, имеющие одинаковые индексы, называются диагональными. Матрица, у которой ниже главной диагонали стоят нули, называется треугольной.

Матрица, состоящая из одной строки, называется матрицей-строкой, а матрица, состоящая из одного столбца – матрицей-столбцом. Обе такие матрицы называют также вектором.

Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается .

Если число строк матрицы равно числу столбцов, то матрица называется квадратной, а число строк (столбцов) порядком матрицы.

Квадратная матрица, у которой только диагональные элементы могут быть не равны нулю, называется диагональной матрицей

Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается .

Матрица, полученная из исходной перестановкой строк со столбцами, называется транспонированной по отношению к исходной и обозначается :.

Заметим, что .

В математике матрица рассматривается как самостоятельный математический объект, с которым можно производить различные действия.

1. Сравнение матриц. Две матрицы равны, если они имеют одинаковый размер и соответствующие элементы равны:

.

2. Умножение матрицы на число. Для того чтобы умножить матрицу на число надо умножить на это число все элементы матрицы:

.

3. Сложение (вычитание) матриц. Сложение (вычитание) матриц проводится поэлементно и возможно для матриц одного размера:

. Для перечисленных выше действий справедливы следующие свойства:

4. Умножение матриц. Матрицы перемножаются по правилу строки на столбец.

Рис.1

А именно, элементы, соединенные одной линией перемножаются, а затем результаты складываются. Для того чтобы получить элемент матрицынадо каждый элемент-ой строки матрицыумножить на соответствующий по порядку элемент- го столбца и результаты сложить.

►Пример 1. Даны матрицы . Найти.

Решение.

.

◄

Умножение матриц возможно только в случае, если число столбцов первой матрицы равно числу строк второй матрицы. Результат умножения – матрица, имеющая число строк, совпадающее с числом строк первой матрицы, и число столбцов равное числу столбцов второй матрицы. При умножении матрицы на вектор-столбец получаем вектор-столбец. При умножении матрицы на транспонированную матрицу получаем квадратную матрицу.

Умножение матриц не коммутативно (см. пример 1). Более того, при перестановке (коммутации) матриц подчас умножение не всегда возможно. Те квадратные матрицы, для которых выполнено свойство , называютсякоммутативными.

Для матриц выполнены ассоциативный и дистрибутивный законы умножения, если не нарушается порядок множителей и умножение возможно. То есть, верны следующие свойства умножения:

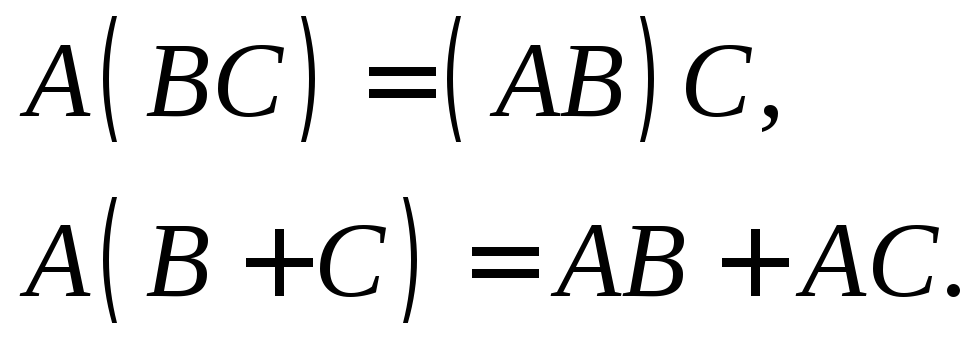
Отметим также свойство умножения для транспонированных матриц

.

5. Возведение в степень. Для квадратных матриц определено возведение в натуральную степень, которое проводится как последовательное умножение. При этом при каждом последующем умножении справедлив коммутативный закон умножения

.

Упражнения.

Даны матрицы:

Выполнить действия:

1) . 2). 3). 4). 5).

Ответы:

1). 2). 3). 4). 5).

6. Вычислить , еслиудовлетворяют условию.Ответ:.

7. Найти , если. Ответ:.

8. Вычислить .Ответ: .