78

Электромагнитные поля и волны. Контрольная работа. Вариант m=7; n=8

Задача № 1

В безграничной однородной среде с параметрами распространяется в направлении орта однородная плоская линейно поляризованная волна частоты , имеющая при z=0 ( т.е. на плоскости x0y) комплексную амплитуду

Требуется:

1. Вычислить тангенс угла диэлектрических потерь и определить характер среды (диэлектрическая, проводящая, полупроводящая).

2. Рассчитать параметры волны (коэффициент ослабления , коэффициент фазы , коэффициент распространения 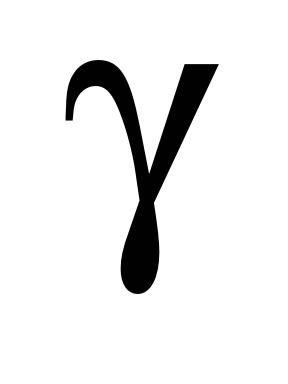, характеристическое сопротивление фазовую скорость длину волны ).

3. Написать формулы комплексных амплитуд полей мгновенных значений 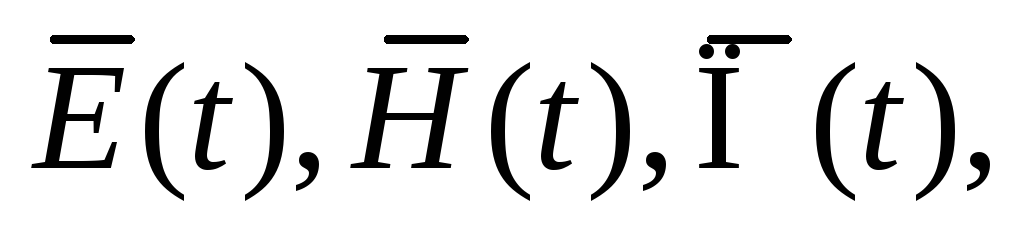среднего за период значения вектора Пойнтинга , подставить в них численные значения и рассчитать.

4. Написать выражения напряженностей для фиксированного момента времени , определяемого условием , и построить для этого момента зависимость структуры полей Е и Н волн от координаты . Результаты расчетов представить в виде таблицы.

5. Определить расстояние при прохождении волной которого амплитуды напряженностей электрического и магнитного полей убывают на дБ.

т	7
	2,6
мВ/м	5
,рад

п	8
,См/м	2∙10–6
Гц	3∙109
дБ	3

Решение

1. Ф/м (1.1) – абсолютная диэлектрическая проницаемость

Абсолютная магнитная проницаемость : (1.2)

(1.3) – тангенс угла диэлектрических потерь.

Так как полученное значение , то характер среды – диэлектрический и для вычисления требуемых величин используем упрощенные формулы.

2. Коэффициент ослабления (1.4)

1/м

Коэффициент фазы (1.5)

= 101,29 рад/м

Коэффициент распространения (1.6)

Характеристическое сопротивление Ом (1.7)

где (1.8)

(1.9)

Фазовая скорость

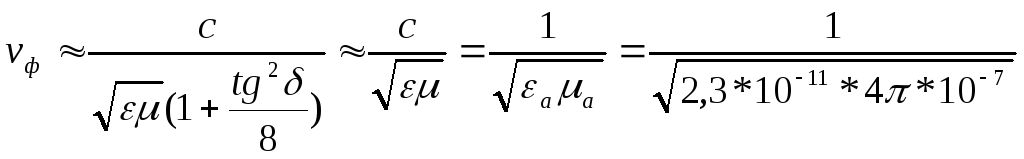= 1,86*10⁸ м/с (1.10)

где ( 1.10, а) – скорость света

Длина волны м. (1.11)

3. Комплексные амплитуды

(2.12)

(1.13)

Мгновенные значения:

(1.14)

(1.15)

Мгновенное значение вектора Пойнтинга:

=

= (1.16)

Значение среднего за период вектора Пойнтинга

=

=0,107exp(-4,68z)cos(0)z⁰=0,107exp(-4,68z)z⁰ (1.17)

4. Для фиксированного момента времени , определяемого условием

(1.18)

(1.19)

Построение зависимостей ( 1.18) и (1.19) приведено в таблице 1 и на рисунках 1 , 2 и 3.

Таблица 1.

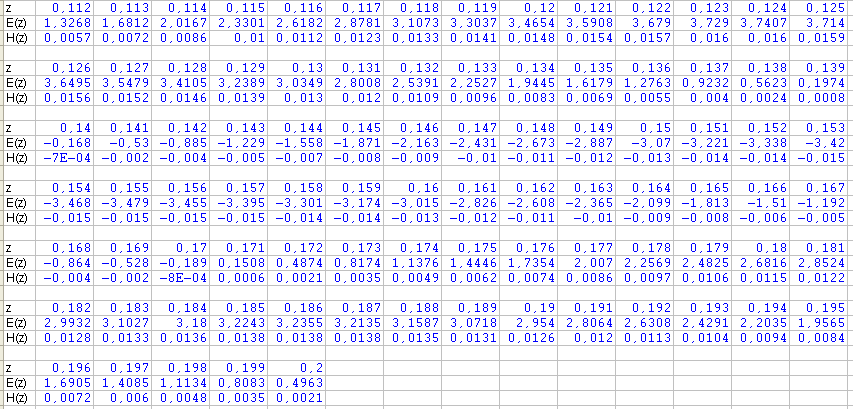
Рисунок 1.

Рисунок 2.

Рисунок 3.

5. м.

Задача № 2

По прямоугольному волноводу, который заполнен воздухом ( Ф/м, Г/м) и имеет длину L, распространяется в одноволновом режиме сигнал, полностью поглощаемый нагрузкой и занимающий полосу частот от до , где - центральная частота полосы). Для бегущей волны основного типа Н₁₀ и частоты в начале волновода (z=0) на его оси (х=а/2; y=b/2)комплексная амплитуда .

Материал волновода:

т	7
Материал стенок	Латунь
ГГц	6,00
кВ/м	1,0
n	7
	0,218
м	12
рад

n	8
	0,198
м	17
рад

Требуется:

1. Определить стандартные поперечные размеры волновода (см. [4 или 5, задача 11.6], а также табл. 2).

Таблица 2

Размеры сечений прямоугольного волновода, а  b, мм

165  82,5	86  43	47,5  22	28,5  12,6	16  8
130  65	72  34	40  20	23  10	13  6,5
109  54,5	58  29	35  16	19  9,5	11  4,3

2. Для этого волновода рассчитать на краях полосы частот сигнала (которой соответствует интервал длин волн от до где ) коэффициент ослабления обусловленный потерей мощности в материале стенок (табл. 3), и коэффициент полезного действия

Таблица 3

Значения удельной электропроводности материала стенок волновода

Материал	Серебро	Медь	Алюминий	Латунь
См/м	5,30∙107	5,25∙107	2,94∙107	1,56∙107

^{Примечание. Для всех материалов}

3. Рассчитать параметры бегущей по волноводу волны Н₁₀ частоты (коэффициент фазы , фазовую скорость v_ф, скорость переноса энергии v_э, длину волны в волноводе характеристическое сопротивление

4. Написать формулы мгновенных значений всех компонент поля бегущей по волноводу волны Н₁₀ частоты Заменить буквенные обозначения известными числовыми значениями величин.

5. Получить выражения всех компонент поля волны Н₁₀ для фиксированного момента времени , определяемого условием, и построить для этого момента картины векторных линий поля в характерных поперечных (z = 0, z = ±/4) и продольных (х = а/2, у = const) сечениях волновода.

Заменив металлические стенки волновода идеальным проводником, построить на их внутренней поверхности картины векторных линий плотности поверхностного электрического тока , которые соответствуют картинам поля Н₁₀.

6. С учетом полученных в п. 5 картин векторных линий определить расположение элементов связи (зонд, петля, узкая щель, прорезанная в стенке) с волной рабочего типа Н₁₀ волновода. Указать их на рисунках п. 5.

1. Размеры поперечного сечения прямоугольных волноводов выбираются в соответствии с заданными полосой частот и мощностью. Обычно прямоугольный волновод работает на основном типе колебаний - волне Н₁₀, в которой электромагнитное поле имеет одну вариацию по широкой стенке волновода «а» и однородно по узкой стенке «b». Как правило, используется соотношение а/b ≥ 2. В этом случае первым высшим типом является волна Н₂₀. Соответствующие критические длины волн: λкр _Н10 = 2а, λкр _Н20 = а. Рабочий диапазон частот ограничен значениями f верх=с/a, fнижн=с/2а, где с – скорость света. Таким образом, максимальная ширина полосы частот определяется из неравенства с/а>f>с/2а, а размер стенки - из соотношений λ₀> а > λ₀/2 где λ₀ =с/f.

Поскольку Гц, Гц (2.1)

Гц (2.2)

Гц (2.3)

м. (2.4)

м. (2.5)

Выбираем размер стенки из соображений (2.6)

В таблице 2 условиям (2.6) соответствует стандартный волновод с размерами сечений

35 х 16 мм.

2. м. (2.7) м. (2.8)

Бегущая волна Н₁₀ характеризуется следующими параметрами :

(2.9)

1/м (2.10)

м. (2.11)

При (2.12)

где Ом (2.13) - активное поверхностное сопротивление металла с проводимостью σ.

Ом (2.14) -характеристическое сопротивление cреды, заполняющей волновод.

Для получим

1/м.

Для получим

1/м

Для получим

1/м

Среднее за период значение мощности бегущей волны типа Н₁₀, проходящая через поперечное сечение волновода в начале (z=0) волновода найдем по формуле:

Вт (2.15)

Среднее за период значение мощности бегущей волны типа Н₁₀, проходящая через поперечное сечение волновода в конце (z=L) волновода найдем по формуле:

Вт (2.16)

Коэффициент полезного действия (2.17)

3. Коэффициент фазы

рад/м (2.18)

Фазовая скорость

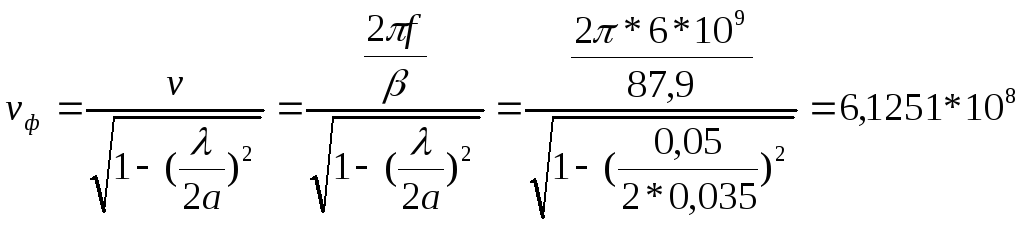м/с (2.19)

Скорость переноса энергии

м/с (2.20)

Длина волны в волноводе

м. (2.21)

Характеристическое сопротивление

Ом (2.22)

4. Формулы мгновенных значений всех компонент поля бегущей по волноводу волны Н₁₀ частоты :

(2.23)

(2.24)

(2.25)

В формулах (2.23 – 2.25) - наибольшее значение амплитуды напряженности электрического поля; - начальная фаза ().

5. Для фиксированного момента времени , определяемого условием выражения для всех компонент поля волны Н₁₀ принимают вид:

(2.26)

(2.27)

(2.28)

Из выражений (2.26 – 2.28) видно, что вектор Е имеет только одну составляющую и не зависит от координату y. Векторные линии Е начинаются и оканчиваются на широких стенках волновода. Вектор Н имеет две составляющие и , следовательно, его векторные линии представляют собой замкнутые петли, которые лежат в сечениях , параллельных плоскости .

На рисунке 4 для поля Н₁₀ по формулам (2.26 – 2.28) построены распределения векторных линий Е и Н в различных сечениях. С течением времени картины векторных линий рис.4 перемещаются со скоростью в направлении распространения волны .

На рисунке 5 изображена картина векторных линий плотности поверхностного электрического тока , которые соответствуют картинам поля Н_10.

6. Щели в стенках волновода излучают только в том случае, когда они перерезают поверхностные токи, протекающие по стенкам волновода (рисунок 6). Из структуры токов в стенках видно, что продольные щели могут прорезаться как в широких, так и в узких стенках волновода. При этом, однако, продольная щель, прорезанная посередине широкой стенки, не излучает, поскольку на средней линии поперечные токи отсутствуют. Поперечные щели можно прорезать только в широких стенках. Наклонные щели можно прорезать как в широких, так и в узких стенках.

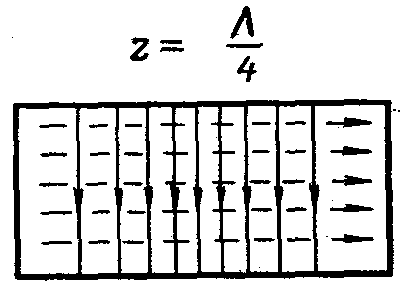
Рисунок 4.

Рисунок 5.

Рисунок 6.

Список литературы

1. Фальковский О.И. Техническая электродинамика.-М.: Связь, 1978

2. Вольман В.И., Пименов Ю.В. Техническая электродинамика.-М.: Связь, 1971

3. Семенов Н.А. Техническая электродинамика.-М.: Связь, 1973

4. Фальковский О.И. Методические указания к практическим занятиям по дисциплине « Электромагнитные поля и волны»/ СПбГУТ. – СПб, 1999

5. Фальковский О.И. Методические указания к практическим занятиям по дисциплине « Техническая электродинамика»/ ЭИС. – СПб, 1992

11