7. Колебания с затуханием в электрическом контуре. Имеется контур.

Напишем закон Ома:

; ;

Всё делим на и записываем в виде.

Решение этого уравнения имеет вид: ;

Здесь и – постоянная интегрирования.

; ;

Найдём закон изменения тока в контуре:

Известно, что , отсюда или

Домножим и разделим выражение для на последнее выражение:

Следовательно ток в контуре опережает по фазе напряжение на конденсаторе больше, чем на , но меньше, чем на

, то колебания в контуре не возникают, а имеют место апериодический разряд конденсатора.

Сопротивление, при котором называется критическим сопротивлением.

Тогда

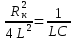
Если колебания возникают.

Если колебания не возникают.

8. Вынужденные колебания механической системы. Резонанс.

Пусть на систему оказывается внешнее воздействие, то есть действует какая-то вынуждающая сила . Рассмотрим простейший случай, когда эта сила совершает гармонические колебания.

Тогда второй закон Ньютона можно записать в виде

Всё делим на и записываем в виде:

Вводим обозначение ; ; ;

- получилось линейное, неоднородное, дифференциальное уравнение.

Как известно, общее решение неоднородного есть сумма общего решения соответствующего однородного и какого-нибудь частного решения неоднородного. Частное не содержит произвольных констант.

Общее решение соответствующего однородного уже известно.

Ищем частное решение неоднородного. Чтобы это сделать, правой части добавим слагаемое.

.

тогда справа будет

и всё подставляем в уравнение

Комплексное число в знаменателе представим в показательном виде:

, где ,

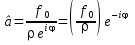
Переходя к вещественной части получается

это время называется временем установления колебаний.

Запишем его в явном виде:

В системе возникли вынужденные гармонические колебания с частотой вынуждающей силы. При этом, амплитуда колебаний зависит от параметров системы и от частоты вынуждающей силы. Фаза колебаний — тоже самое. Вынужденные колебания отстают по фазе от внешнего воздействия. При какой-то частоте амплитуда колебаний резко возрастает, эта частота называется резонансной, а явление возрастания амплитуды — резонансом. Чтобы найти , нужно амплитуду умножить на экстремум. Нас интересует , при котором подкоренное выражение минимально.

Берём производную от подкоренного выражения и приравниваем её нулю:

Можно найти амплитуду при резонансе:

Видно, что при ;

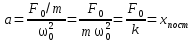
- смещение под действием постоянной силы, равное амплитуде внешнего воздействия.

всегда меньше

тем меньше , тем меньше затухание

Изобразим зависимость амплитуды колебаний от частоты (так называемые резонансные кривые).

Если резонанс не возникает.

Для малых найдём отношение амплитуды при резонансе к смещению под действием постоянной силы.

для малых затуханий добротность показывает во сколько раз амплитуда при резонансе больше смещения под действием постоянной силы, равной амплитуде внешнего воздействия.