1. Гармонические колебания и их характеристики. Скорость и ускорение колеблющейся точки.

Гармонические колебания — это простейший вид колебаний и любой сложный колебательный процесс может быть представлен конечной или бесконечной суммы гармонических колебаний (фрианализ).

В физике важное место занимает периодическое движение, когда одно и тоже движение повторяется много раз который называется, среди периодических движений называются колебания, когда, например, материальная точка движется по отрезку дуги или прямой вперёд или назад, между двумя крайними положениями.

— дуговая координата колеблющейся точки, или смещение точки от положения равновесия.

Среди колебаний особо выделяются гармонические колебания это такие колебания. При которых S изменяется во времени по закону синуса или косинуса.

— наибольшее смещение или амплитуда колебаний.

Всё, что стоит под синусом или косинусом, называется фазой колебаний. Фаза, для данного момента времени, определяет положение и направление движения колеблющейся точки.

• — циклическая частота

— текущее время

— начальная фаза, определяет положение направления движения в начальный нулевой момент времени.

и связаны стандартным образом.

;Гц;

— связь циклической частоты. Число колебаний за секунды.

Пусть колебания совершаются вдоль кривой линии. Направим вдоль неё ось . Начало координат поместим в положение равновесия. И когда уравнение незатухающих гармонических колебаний можно записать так:

Скорость и ускорение колеблющейся точки.

То есть скорость совершает гармонические колебания с той-же частотой и амплитудой .

, поэтому говорят, что скорость опережает смещение по фазе на или на четверть периода.

;

;

Вывод: при максимальном смещении, скорость колеблющейся точки обращается в ноль.

;

;

Вывод: колеблющаяся точка положение равновесия проходит с максимальной скоростью

Смещение ускорения колеблется в противофазе.

Выражение для можно представить в виде

2. Свободные колебания упругой механической системы без затухания. Энергия колебательной системы.

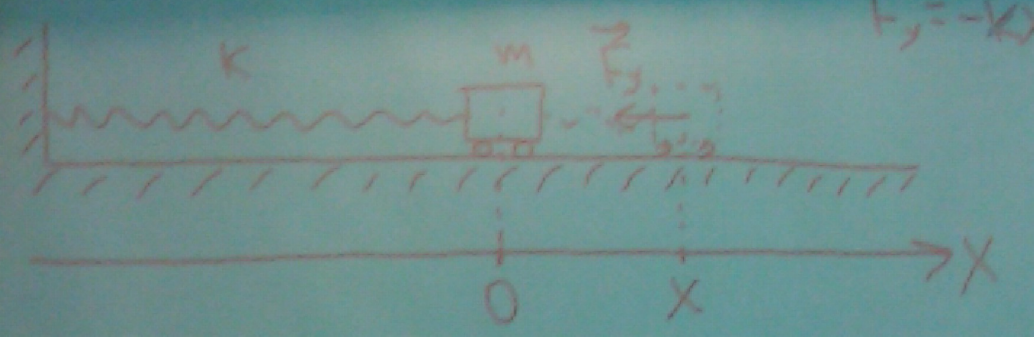
Установим характер движения тела, чтобы это сделать, напишем второй закон Ньютона (в проекции на ось ).

- это дифференциальное уравнение свободных незатухающих гармонических колебаний.

Решение этого уравнения имеет вид:

Вывод: под действием упругой силы в системе возникают незатухающие гармонические колебания с частотой и периодом .

То есть параметры системы и полностью определяют частоту и период колебаний.

и — постоянные интегрирования.

Энергия колебательной системы включает в себя кинетическую энергию движущегося тела и потенциальную энергию.

Вывод: полная энергия колебательной системы остается постоянной.

3. Колебания без затухания в электрическом контуре.

За положительное направление тока принимается ток заряда конденсатора.

Напишем закон Ома: ,

(из определения ёмкости конденсатора).

; контур идеальный.

, всё делим на и записываем в виде:

Обозначим через ,

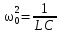Решение уравнения имеет вид:

Вывод: в контуре возникают свободные, незатухающие колебания, с частотой колебания и периодом колебания (формула Томсона), следовательно параметры контура полностью определяют частоту и период свободных, незатухающих колебаний.

Закон его изменения находим из определения ёмкости конденсатора.

Обозначим через . Заряд и напряжение колеблются в фазе.

Найдём закон изменения тока в контуре.

, избавимся от минуса и перейдём к косинусу, следовательно ток в контуре совершает колебания с той-же самой частотой . При этом ток опережает по фазе напряжение на конденсаторе на или на четверть периода. Видно, что ток максимален, когда напряжение на конденсаторе равно нулю и ток обращается в ноль при максимальном напряжении.