Дополнительные свойства проверочной матрицы.

1. Из выражения и из определения проверочной матрицы следует, что произведение кодовой последовательностиV на Н^T равно нулю.

- синдром ошибки, если , то есть ошибка.

S = 0 – разрешённая комбинация.

2. Умножение V на Н сводится к суммированию столбцов Н, соответствующих единицам в умножаемой комбинации. Следовательно кодовой комбинации min веса соответствует minчисло столбцов, в сумме дающих чисто нулевой столбец, т.е. min кодовое расстояние группового кода, равное min числу линейно зависимых столбцов в проверочной матрице.

Методы кодирования и декодирования групповых кодов.

1. Методы кодирования.

а) На основе порождающей матрицы.

Известны данные пользователя u и то, что код разделимый :

r u

n-k k

Пример.

Код (5,3), , u = 101

складываем те строки в G, где в u стоят единицы.

б) На основе проверочной матрицы.

Известна информационная часть.

Вывод:

Если число избыточных символов меньше, чем число информационных символов, то удобнее кодировать по способу б), иначе по а).

П

r1 r2 r3 r4 r5

ример.

r u

n-k k

u = 101

r₁ = u₁ + u₂ = 1

r₂ = u₂ + u₃ = 1

V = 11101

Или

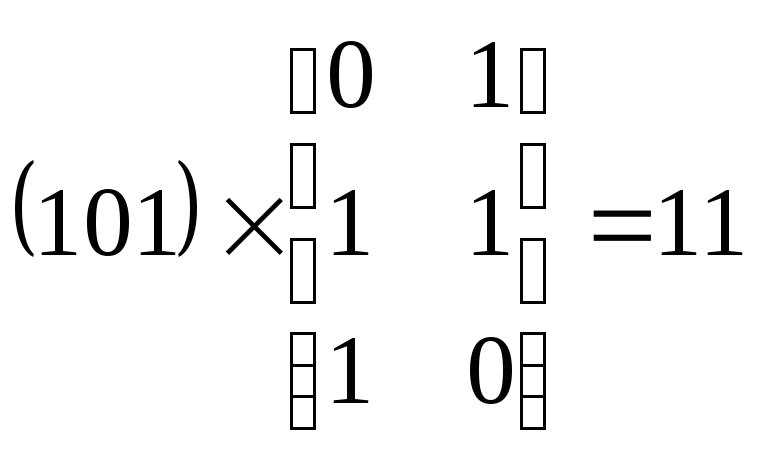
2. Методы декодирования.

- синдром ошибки, если , то есть ошибка. Чтобы её исправить нужно привязать конкретный синдром к конкретному образцу ошибки. S – вектор из n-k. Тогда всего возможно 2^n-k – значений синдрома.

Пусть передавалась кодовая комбинация V, а была принята V`. V` = V + R, где R – образец ошибки. Тогда .- если не совпадает с видом кодовой комбинации, иначе тоже равно нулю.

Связь между e ошибок и синдромами устанавливается с помощью таблицы декодирования (разложение группы по подгруппам на смежные классы). Таблица декодирования содержит 2^n-k строк и 2^k столбцов.

V0 = (00…0)	V1	V2	…	Vi	…	V2k-1
e1 = (10…0)	V1 + e1	V2 + e1	…	Vi + e1	…	V2k-1 + e1
e2 = (010…0)	V1 + e2	V2 + e2	…	Vi + e2	…	V2k-1 + e2
			2n
e2n-k-1	V1 + e2n-k-1					V2k-1 + e2n-k-1

e₁ = (10…0) – лидер смежного класса.

Если d_min = 3, то в эту таблицу не вошли коды веса 1 и 2. e₁ ни в одном помехоустойчивом коде, т.к. d_min = 1. Будут перечислены все возможные варианты искажений 2ⁿ и только один раз. В качестве первого столбца – комбинации min веса, не вошедшие в верхние строчки. Для каждого образца ошибки появляется свой индивидуальный синдром.

Метод максимального правдоподобия.

Выход декодера

Вход декодера

Всего ошибок: 2ⁿ – 2^k

Может исправить: 2^n-k

Может обнаружить: 2ⁿ – 2^k