
- •Введение
- •1. Матрицы и действия с матрицами
- •2. Определители
- •3. Обратная матрица. Решение матричных уравнений
- •4. Ранг матрицы
- •5. Системы линейных уравнений. Основные понятия
- •6. Решение линейных систем по формулам Крамера
- •7. Решение систем с помощью обратной матрицы
- •8. Исследование систем линейных уравнений. Метод Гаусса
- •9. Однородные системы
- •10. Собственные значения и собственные векторы матрицы
- •11. Действия с матрицами на компьютере в excel
- •12. Решение систем линейных уравнений в excel
- •Индивидуальное задание
6. Решение линейных систем по формулам Крамера
Теорема Крамера.
Пусть дана система, в которой число уравнений совпадает с числом неизвестных
 (10)
(10)
Если определитель основной матрицы системы
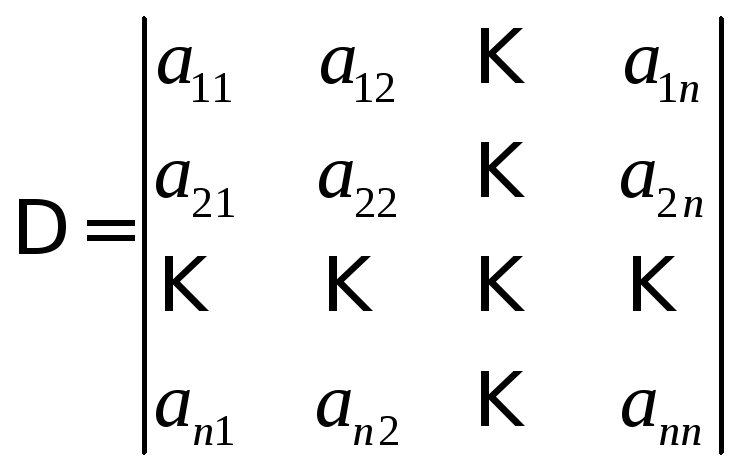 ,
(11)
,
(11)
не равен нулю, то
система имеет единственное решение и
![]() ,
где
,
где
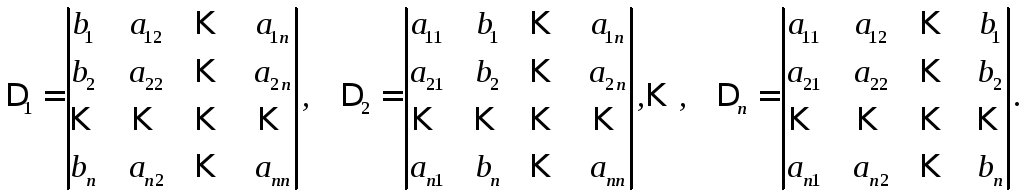
Определители
![]() ,
получены из определителя (11) заменой
соответствующего столбца на столбец
свободных членов.
,
получены из определителя (11) заменой
соответствующего столбца на столбец
свободных членов.
►Пример 8. По
формулам Крамера найти решение системы
уравнений

Решение.
Вычислим определители и найдем решение
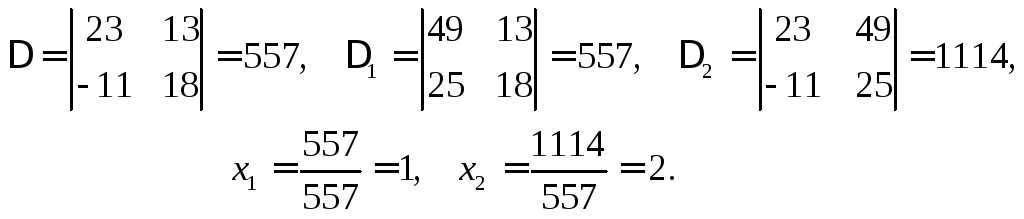
Ответ:
![]() .◄
.◄
Упражнения.
Решить системы по формулам Крамера:
1)
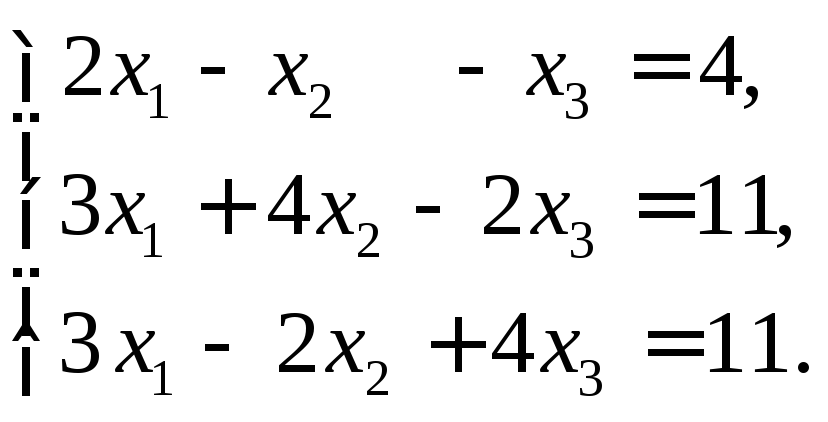 2)
2) 3)
3)
Ответы:
1)![]() ,
2)
,
2)![]() ,
3)
,
3)![]() .
.
7. Решение систем с помощью обратной матрицы
Система из
![]() уравнений с
уравнений с![]() неизвестными (10) в матричной форме
имеет вид (5)
неизвестными (10) в матричной форме
имеет вид (5)
![]() ,
,
где
 ,
, ,
, .
.
Если матрица
![]() невырожденная, то система имеет
единственное решение, которое вычисляется
по формуле
невырожденная, то система имеет
единственное решение, которое вычисляется
по формуле![]() .
.
►Пример 9. С помощью обратной матрицы найти решение системы
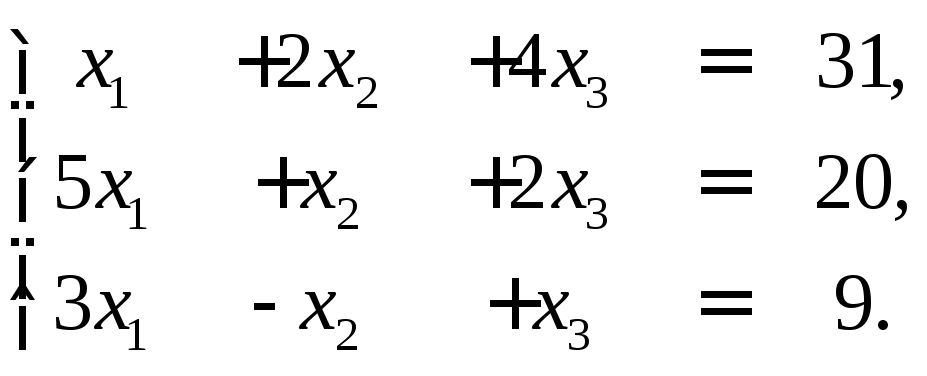
Решение.
Проведем необходимые вычисления:


 .
.
Ответ:![]() .
◄
.
◄
Упражнения.
Найти решение систем с помощью обратной матрицы:
а)
 б)
б) в)
в)
г)
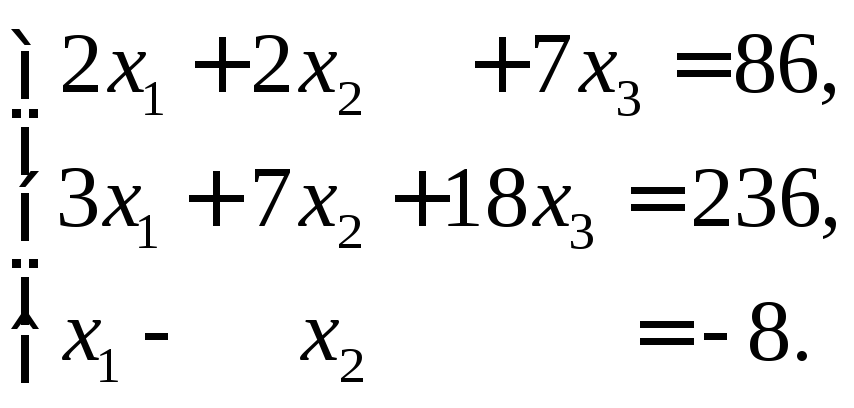 Ответы:
а)
Ответы:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() г)
г)![]() .
.
8. Исследование систем линейных уравнений. Метод Гаусса
Рассмотрим линейную систему общего вида:
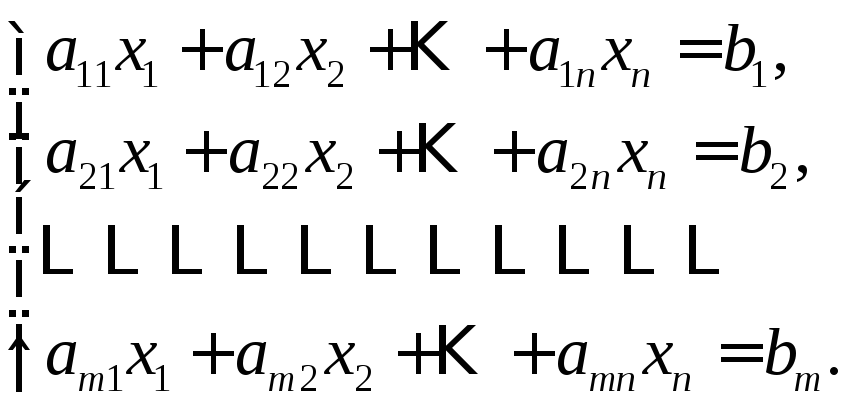
Теорема Кронекера-Капелли.
Для совместности
системы линейных уравнений необходимо
и достаточно, чтобы ранг ее основной
матрицы (![]() )
был равен рангу расширенной матрицы
(
)
был равен рангу расширенной матрицы
(![]() ).
).
Пусть
![]() =
=![]() =
=![]() .
Тогда верны следующие утверждения.
.
Тогда верны следующие утверждения.
Следствие
1. Если ранг
матрицы
![]() равен числу неизвестных
равен числу неизвестных![]() ,
то система имеет единственное решение.
,
то система имеет единственное решение.
Следствие
2. Если ранг
матрицы
![]() меньше числа неизвестных, то система
имеет бесконечное множество решений.
При этом
меньше числа неизвестных, то система
имеет бесконечное множество решений.
При этом![]() неизвестных, которые называются
свободными, принимают произвольные
значения. Говорят, что система имеет
неизвестных, которые называются
свободными, принимают произвольные
значения. Говорят, что система имеет![]() степеней свободы.
степеней свободы.
Метод Гаусса (исключение неизвестных) состоит в том, что с помощью умножения уравнений на ненулевые числа и сложения в первом уравнении оставляем все неизвестные, во втором на одно меньше, в третьем на два меньше и т.д. Эту операцию (назовем ее процедурой Гаусса) удобно проводить, используя матрицы.
Составим расширенную матрицу системы и отделим для удобства свободные члены вертикальной линией. С помощью элементарных преобразований приводим матрицу к треугольному виду. Элементарные преобразования матрицы проводим только для строк.
Умножая первую строку на соответствующие коэффициенты и прибавляя к лежащим ниже строкам, получим нули в первом столбце. Затем проделываем такую же процедуру со второй строкой, третьей и т.д., до предпоследней строки. В результате преобразований получаем матрицу, по которой можно записать систему, равносильную исходной.
Рассмотрим три ситуации, возникающие при исследовании линейных систем.
1)
![]() .Система
несовместна.
.Система
несовместна.
►Пример 10.
Решить систему уравнений методом Гаусса:

Решение.
Составим расширенную матрицу и преобразуем ее:
 .
.
Как и в примере 2 над стрелочкой указаны выполняемые операции.
Для удобства вычислений переставим четвертую строку на место второй и за счет второй строки получим нули во втором столбце во всех строках ниже второй, а затем за счет третьей строки - в третьем столбце:

В четвертой строке легко было получить нули, умножив третью строку на минус единицу и прибавив ее к четвертой. Мы не упрощали вычислений, чтобы сохранить алгоритм получения нулей в нижележащих строках за один шаг.
По преобразованной
матрице определяем ранги:
![]() ,
,![]() ,
следовательно, данная система уравнений
несовместна.
,
следовательно, данная система уравнений
несовместна.
.
Ответ: система не имеет решений. ◄
2)
![]() .Система
совместна и имеет единственное решение.
В результате преобразований приходим
к ступенчатой системе, решение которой
легко находится.
.Система
совместна и имеет единственное решение.
В результате преобразований приходим
к ступенчатой системе, решение которой
легко находится.
►Пример 11. Решить систему уравнений методом Гаусса

Решение.
Составим расширенную матрицу и преобразуем ее:


Ранг основной
матрицы равен рангу расширенной матрицы
![]() и равен числу неизвестных. Следовательно,
система совместна и имеет единственное
решение. По преобразованной матрице
составляем систему, равносильную
исходной
и равен числу неизвестных. Следовательно,
система совместна и имеет единственное
решение. По преобразованной матрице
составляем систему, равносильную
исходной

Полученная система имеет ступенчатый вид и легко решается.
Ответ:
![]() .◄
.◄
3)
![]() .Система
совместна, но имеет бесконечное множество
решений. Это множество решений находим,
перенося члены со свободными неизвестными
в правую часть уравнений.
.Система
совместна, но имеет бесконечное множество
решений. Это множество решений находим,
перенося члены со свободными неизвестными
в правую часть уравнений.
Рассмотрим запись решения таких систем в матричной форме.
Пусть дана система

и известно, что
![]() .
Тогда система имеет
.
Тогда система имеет![]() степеней свободы, т.е.
степеней свободы, т.е.![]() неизвестных принимают произвольные
значения, а
неизвестных принимают произвольные
значения, а![]() неизвестных выражаются через них.
Минор, не равный нулю, напоминаем,
называетсябазисным.
Не уменьшая общности, будем считать,
что базисный минор системы занимает в
ней верхний левый угол. Обозначим этот
минор
неизвестных выражаются через них.
Минор, не равный нулю, напоминаем,
называетсябазисным.
Не уменьшая общности, будем считать,
что базисный минор системы занимает в
ней верхний левый угол. Обозначим этот
минор
![]() :
:
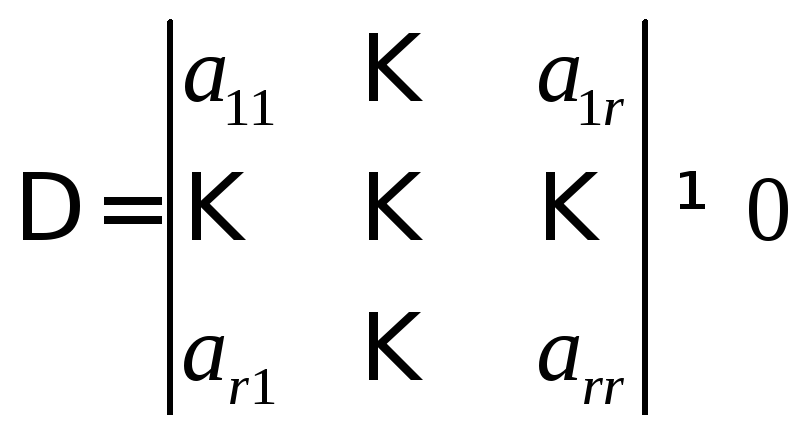 .
.
Минор
![]() является базисным и для матрицы
является базисным и для матрицы![]() ,
поэтому строки с номерами
,
поэтому строки с номерами![]() являются линейными комбинациями первых
являются линейными комбинациями первых![]() строк и система эквивалентна системе
из
строк и система эквивалентна системе
из![]() уравнений (свободные неизвестные
перенесены в правую часть)
уравнений (свободные неизвестные
перенесены в правую часть)

Решая эту систему по методу Крамера, имеем
![]() ,
,
где
 −определитель,
полученный из базисного заменой
−определитель,
полученный из базисного заменой
![]() го
столбца на столбец правой части системы.
Пользуясь свойствами определителей,
имеем
го
столбца на столбец правой части системы.
Пользуясь свойствами определителей,
имеем
![]() .
(11)
.
(11)
Символ:
![]() ,-
означает, что
,-
означает, что![]() −ый
столбец базисного минора заменен на
столбец коэффициентов при неизвестном
−ый
столбец базисного минора заменен на
столбец коэффициентов при неизвестном![]() .
Введем обозначения:
.
Введем обозначения:
![]() .
.
Тогда
![]() .
.
Добавим сюда
![]() очевидных равенств
очевидных равенств![]() .
.
Тогда множество решений системы можно записать в виде:
 (12)
(12)
Для вычисления
![]() полагаем свободные неизвестные равными
нулю. Для вычисления
полагаем свободные неизвестные равными
нулю. Для вычисления![]() полагаем свободные члены равными нулю,
полагаем свободные члены равными нулю,![]() ,
а остальные свободные неизвестные
равными нулю.
,
а остальные свободные неизвестные
равными нулю.
. Выбор свободных
неизвестных, вообще говоря, можно делать
по-разному. Однако не всякие
![]() неизвестных можно принять за свободные.
Необходимо, чтобы коэффициенты при
остальных
неизвестных можно принять за свободные.
Необходимо, чтобы коэффициенты при
остальных![]() неизвестных составили базисный минор.
неизвестных составили базисный минор.
►Пример 12. Решить систему уравнений

Решение.
Преобразуем расширенную матрицу системы

 .
.
Ранг основной
матрицы равен рангу расширенной матрицы
![]() ,
число неизвестных равно пяти. Следовательно,
система совместна, но имеет бесконечное
множество решений. Число степеней
свободы равно двум. Выберем свободными
неизвестными
,
число неизвестных равно пяти. Следовательно,
система совместна, но имеет бесконечное
множество решений. Число степеней
свободы равно двум. Выберем свободными
неизвестными![]() и выразим
и выразим![]() через них:
через них:
![]()
 отсюда получаем
отсюда получаем

Ответ запишем в виде вектора-столбца.
Ответ: .
◄
.
◄
Получим также
решение заданной системы, используя
формулу (12). Положим
![]() .
.![]()
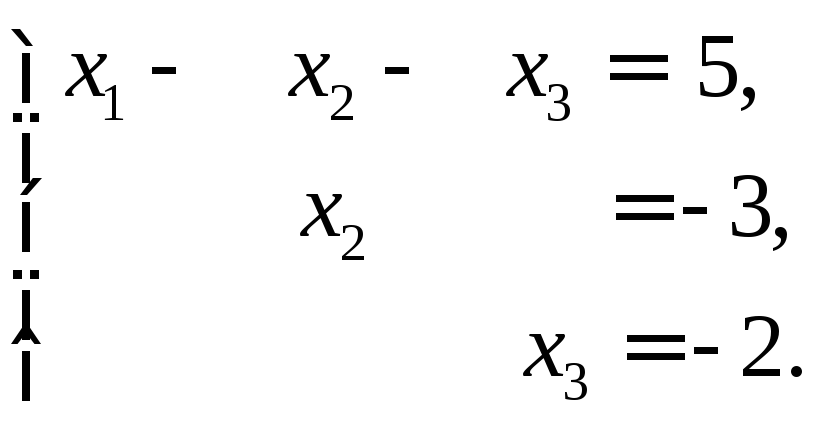 Получаем вектор
Получаем вектор
![]() .
.
Положим
![]() .
.
 Получаем вектор
Получаем вектор
![]() .
.
Положим
![]() .
.
 Получаем вектор
Получаем вектор
![]() .
.
Окончательное
решение:
 ◄
◄
Упражнения.
Исследовать и решить системы уравнений:
1.
 Ответ:
Ответ:
![]() .
.
2.
 Ответ:
Ответ:
 .
.
3.
 Ответ:
Ответ:
![]() .
.
4.
 Ответ:
Ответ:
![]() .
.
5.
 Ответ:
Ответ:
![]() .
.
6.
 Ответ:
Ответ:
![]() .
.
7.
 Ответ:
Ответ:
![]() .
.
8.
 Ответ:
Ответ:
![]() .
.
9.
 Ответ:
Ответ:
![]() .
.
10.
 Ответ:
Ответ:
 .
.
11.
 Ответ:
Ответ:
 .
.
12.
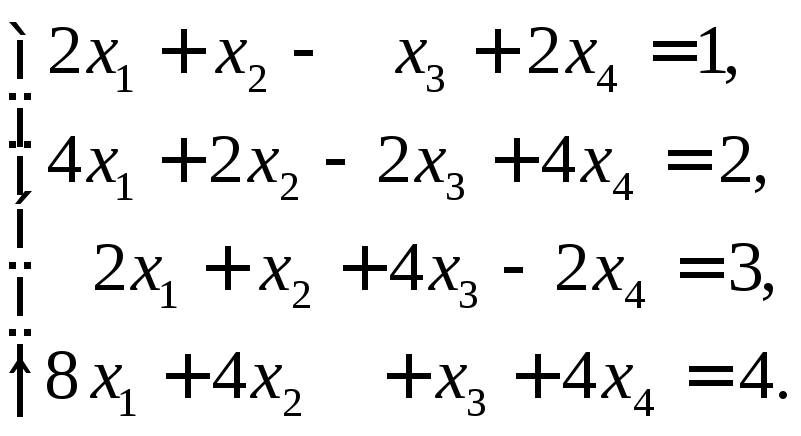 Ответ:
Ответ:
![]() .
.
13.
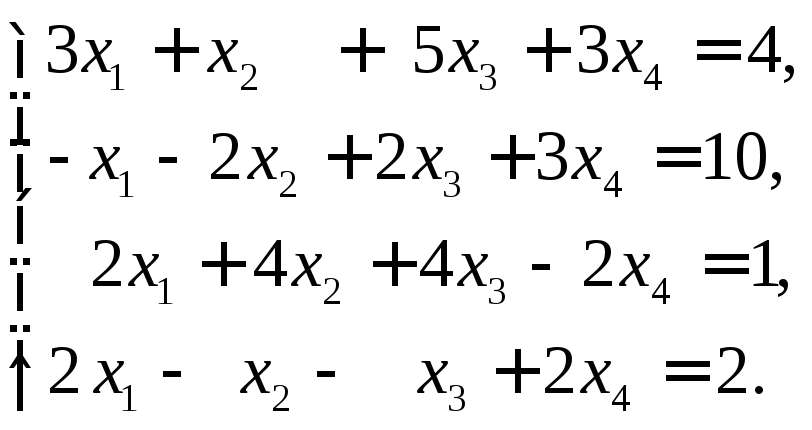 Ответ:
Ответ:
![]()
