
- •Лабораторная работа № 1 Изучение одноканальной замкнутой системы массового обслуживания
- •Лабораторная работа № 2 Изучение многоканальной замкнутой системы массового обслуживания
- •2.1 Цель работы
- •2.2 Краткие сведения об объекте моделирования
- •2.3 Порядок выполнения работы
- •Лабораторная работа № 3 Изучение одноканальной замкнутой смо с ожиданием
- •3.1 Цель работы
- •3.2 Краткие сведения об объекте моделирования
- •3.4 Порядок выполнения работы
- •1,946 1,94 1,949
- •4.3 Порядок выполнения работы
- •Лабораторная работа № 5 [3] Исследование элементов системы моделирования gpss/pc на имитационных моделях массового обслуживания
- •5.1 Цель работы
- •5.2 Краткие сведения об объекте моделирования
- •5.3 Порядок выполнения работы
- •5.4 Задания к работе
- •Лабораторная работа № 6 [3] Исследование на имитационной модели процесса передачи данных в информационно-вычислительной сети
- •6.1 Цель работы
- •6.2 Краткие сведения об объекте моделирования
- •6.3 Порядок выполнения работы
- •6.4 Задание к работе
- •Лабораторная работа № 7 [3] Исследование на имитационной модели процесса функционирования концентратора сети интегрального обслуживания
- •7.1 Цель работы
- •7.2 Краткие сведения об объекте моделирования
- •7.3 Порядок выполнения работы
- •7.4 Задание к работе
- •Лабораторная работа № 8 Построение математических моделей экспериментально-статистическими методами (метод наименьших квадратов)
- •8.1 Цель работы
- •8.2 Краткие сведения об объекте моделирования
- •X –3 –1 1 3
- •8.3 Порядок выполнения работы
- •Требования к оформлению отчета
- •Список литературы
X –3 –1 1 3
y 5 1 –2 –3
В
первом столбце матрицы плана во всех
строках стоят значения
![]() ,
во втором столбце значениях,
в третьем значения х2.
Окончательно эта матрица имеет вид:
,
во втором столбце значениях,
в третьем значения х2.
Окончательно эта матрица имеет вид:
 .
.
Система нормальных уравнений получится по формуле (8.11)
 .
.
Определитель матрицы системы нормальных уравнений
 .
.
 ;
;
 ;
; .
.
Откуда
![]() ;
;
![]() ;
;![]()
или
![]() .
.
Окончательно
![]() .
.
При
большом числе искомых параметров
построение регрессионного уравнения
требует громоздких вычислений. В связи
с этим в настоящее время построение
регрессионных зависимостей практически
всегда производится с применением ЭВМ.
В этом случае удобно использовать
матричный способ представления и
обработки информации. Нетрудно убедиться,
что матрица коэффициентов левых
частей системы равна произведению
матрицы
![]() на транспонированную матрицу
на транспонированную матрицу![]() :
:
|
|
(8.12) |
Вектор-столбец
правых частей системы нормальных
уравнений равен произведению
![]() ,
где
,
где![]() – вектор (8.4)
– вектор (8.4)
|
|
(8.13) |
В матричных обозначениях решение системы (8.11) имеет вид
|
|
(8.14) |
где
индекс – 1 есть символ обращения матрицы;
![]() – вектор исходных параметров. Это
соотношение и используется для нахождения
параметров модели.
– вектор исходных параметров. Это
соотношение и используется для нахождения
параметров модели.
Отметим, что если объект имеет несколько выходных координат, то для каждой выходной координаты ее зависимость от входных переменных находится отдельно.
Проверка адекватности модели
П
Рис.
8.4. Прямая и парабола, проведенные по
точкам
Для
количественной оценки вводится мера
разброса данных дисперсия. Мерой
разброса опытных данных относительно
модели является остаточная дисперсия
![]() ,
равная отношению минимальной суммы
квадратов отклоненийS
к числу степеней свободы.
,
равная отношению минимальной суммы
квадратов отклоненийS
к числу степеней свободы.
Числом степеней свободы называют разность между числом экспериментов и числом неизвестных параметров, оцениваемых на основании этих экспериментов. Окончательно, выражение для остаточной дисперсии
|
|
(8.15) |
где
f
число степеней свободы (![]() ;n
–
число экспериментов; р
– число оцениваемых параметров).
;n
–
число экспериментов; р
– число оцениваемых параметров).
Для
оценки величины случайной ошибки
эксперимента рассчитывают дисперсию
воспроизводимости
![]() .
Для этого проводят одну или несколько
серий параллельных опытов; в каждой
такой серии значения входных переменных
от опыта к опыту не меняются. В этом
случае отклонения относят к среднему
значению измеряемой величины. А число
степеней свободы будет на единицу меньше
числа параллельных опытовm.
.
Для этого проводят одну или несколько
серий параллельных опытов; в каждой
такой серии значения входных переменных
от опыта к опыту не меняются. В этом
случае отклонения относят к среднему
значению измеряемой величины. А число
степеней свободы будет на единицу меньше
числа параллельных опытовm.
Формула
![]() объясняется в данном случае так же, как
и формула дляf
при описании уравнениями: единица
наименьшее число опытов, необходимое
для того, чтобы составить представление
о среднем значении определяемой величины
объясняется в данном случае так же, как
и формула дляf
при описании уравнениями: единица
наименьшее число опытов, необходимое
для того, чтобы составить представление
о среднем значении определяемой величины
Итак
|
|
(8.16) |
где
![]() –
среднее значение у всех результатов
экспериментов.
–
среднее значение у всех результатов
экспериментов.
|
|
(8.17) |
Для проверки адекватности рассчитывают дисперсионное отношение F
|
|
(8.18) |
Если
F
больше некоторого критического значения,
то уравнение неадекватно, если меньше,
то адекватно. Критическое значение F
зависит от двух чисел степеней свободы:
![]() ,
входящего в формулу (8.15),
,
входящего в формулу (8.15),![]() ,
входящего в формулу (8.16).
,
входящего в формулу (8.16).
Чем
меньше
![]() ,
тем больше критическоеF:
чем меньше число степеней свободы при
оценке дисперсии воспроизводимости,
тем эта оценка менее точна и тем менее
определенно приходится оценивать
адекватность: не исключено, что даже
очень большой разброс объясняется
ошибкой опыта. Во всяком случае для
оценки
,
тем больше критическоеF:
чем меньше число степеней свободы при
оценке дисперсии воспроизводимости,
тем эта оценка менее точна и тем менее
определенно приходится оценивать
адекватность: не исключено, что даже
очень большой разброс объясняется
ошибкой опыта. Во всяком случае для
оценки
![]() целесообразно провести не менее трех
опытов (
целесообразно провести не менее трех
опытов (![]() ).
).

 .
. .
.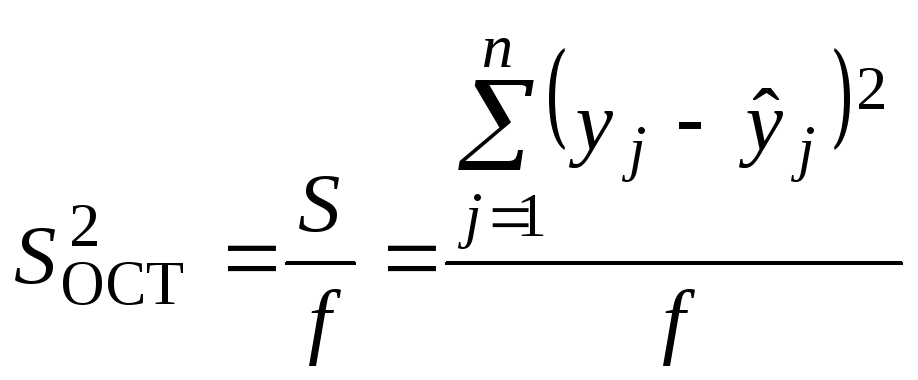 ,
, ,
, ,
, ,
,