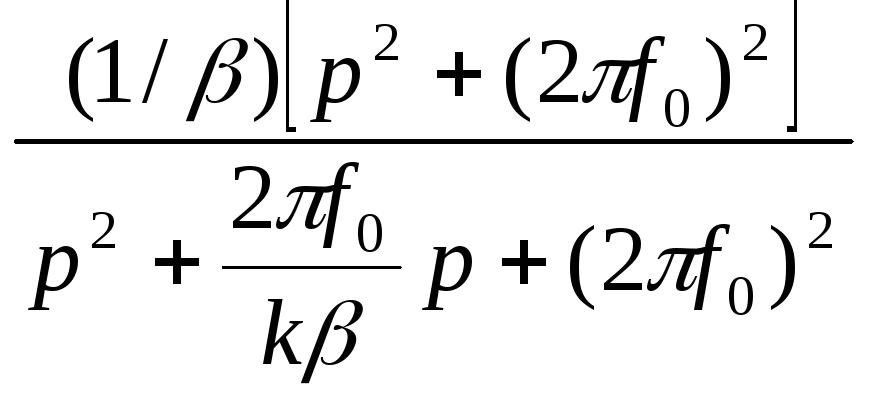- •Часть 3
- •Удк 621. 372. 061
- •Составлены в соответствии с программой дисциплины «Основы теории
- •Часть 3.
- •1. Расчет lc фильтра
- •В результате решения задачи 1 требуется составить пояснительную за-писку с подробным изложением процедуры расчета lc фильтра, в которой:
- •1.2. Указания к решению задачи 1
- •1.2.1.Проектирование схемы фильтра
- •1.2.2. Определение передаточной функции фильтра
- •1.2.3. Расчет характеристики ослабления
- •1.2.4. Моделирование lc фильтра на пк
- •2.Расчет активного rc фильтра
- •2.1. Содержание задания
- •2.2. Указания к выполнению задачи 2
- •2.2.1 Построение схемы фильтра
- •2.2.2 Расчет параметров элементов arc фильтра
- •2.2.3 Расчет частотных зависимостей параметрических
- •Подставив численные значения параметров элементов, получим
- •2.2.4 Расчет характеристики ослабления arc фильтра на пк
- •3. Вопросы для подготовки к защите курсовой работы
- •Содержание
- •Раздел 1. Расчет lCфильтра……………………………………………………… 4
- •Раздел 2.Расчет активного rc фильтра………………………………………….. 19
- •Раздел 3. Вопросы для подготовки к защите курсовой работы……………….. 46
1.2.2. Определение передаточной функции фильтра
Передаточная функция полиноминального ФПНЧ определяется выраже- ниием
![]() ,
(1.10)
,
(1.10)
где
![]() - полином Гурвица степениn.
- полином Гурвица степениn.
Коэффициент
![]() в (1.10) определяет величину ослабления
фильтра на ча-стоте
в (1.10) определяет величину ослабления
фильтра на ча-стоте![]() .
Для ФПНЧ с характеристикой Баттерворта
любого порядка при
.
Для ФПНЧ с характеристикой Баттерворта
любого порядка при![]() дБ
дБ![]() Для ФПНЧ с характеристикой Чебышева
приа= 1,25
дБ :
Для ФПНЧ с характеристикой Чебышева
приа= 1,25
дБ :
![]()
![]()
![]()
![]()
![]()
![]() .
.
Индекс при![]() означает порядокn
ФПНЧ.
означает порядокn
ФПНЧ.
При других значениях неравномерности
асомножители
полиномов Гур-вица и значения коэффициента![]() могут быть получены по формулам,
приве-денным в Приложении 2.
могут быть получены по формулам,
приве-денным в Приложении 2.
В табл.1.11 и 1.12 приведены сомножители
полиномов
![]() для ФПНЧ с характеристиками Баттерворта
и Чебышева, параметры которых даны
в табл. 1.61.9.
для ФПНЧ с характеристиками Баттерворта
и Чебышева, параметры которых даны
в табл. 1.61.9.
Таблица 1.11
Сомножители полинома Гурвица для ФПНЧ с характеристикой
Баттерворта при а = 3 дБ
|
n |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
Таблица 1.12
Сомножители полинома Гурвица для ФПНЧ с характеристиками
Чебышева при а= 1,25 дБ
|
n |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
Передаточная функция проектируемого
фильтра
![]() находится час-тотным преобразованием
передаточной функции
находится час-тотным преобразованием
передаточной функции![]() низкочастотного филь- тра-прототипа.
Формулы преобразования приведены в
табл.1.13.
низкочастотного филь- тра-прототипа.
Формулы преобразования приведены в
табл.1.13.
Следует обратить внимание на то, что
порядок передаточных функций
![]() полосно-пропускающих и полосно-задерживающих
фильтров вдвое пре- вышает порядок их
низкочастотных прототипов. Поэтому
полином
полосно-пропускающих и полосно-задерживающих
фильтров вдвое пре- вышает порядок их
низкочастотных прототипов. Поэтому
полином![]() ,
полу-ченный частотным преобразованием
полинома
,
полу-ченный частотным преобразованием
полинома![]() второго порядка, содержит
второго порядка, содержит
два квадратичных сомножителя:
![]()
Для вычисления коэффициентов
квадратичных сомножителей полинома
![]() можно воспользоваться следующим
алгоритмом:
можно воспользоваться следующим
алгоритмом:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() ,
,
где для
ППФ:
![]() ,
,![]() ;
для ПЗФ:
;
для ПЗФ:![]()
![]() .
.
Следует помнить, что коэффициенты
![]() полинома ГурвицаV(p)
должны быть вещественными положительными.
полинома ГурвицаV(p)
должны быть вещественными положительными.
|
Передаточная
функция ФПНЧ
|
Формула преобразо- вания |
Передаточная функция фильтра
|
Тип фильтра |
|
|
|
|
ФНЧ |
|
|
|
|
ФВЧ |
|
|
|
|
ППФ |
|
|
|
|
ПЗФ |
Таблица 1.13