3. Вопросы для подготовки к защите курсовой работы
1.Как классифицируют электрические фильтры в зависимости от взаимного
расположения полос пропускания и задерживания?
2.Как определяется ослабление фильтра при двусторонней и одностороней
нагрузках? Что такое рабочее ослабление?
3.Что вам известно о расположении полюсов и нулей передаточных функций
устойчивых цепей?
4.Как найти передаточную функцию лестничной электрической цепи?
5.Дайте определение полинома Гурвица и перечислите его основные свойства.
6.Какими основными свойствами обладают амплитудно-квадратичные харак-
теристики? Как определить передаточную функцию цепи по ее АКХ?
7.Какие методы аппроксимации используются в типовых задачах синтеза
линейных электрических цепей?
8.Запишите выражения для АКХ и ослабления полиномиального ФНЧ с ха-
рактеристиками Баттерворта, постройте график ослабления.
9.Запишите выражения для АКХ и ослабления полиномиального ФНЧ с
равноволновыми характеристиками. Как выглядит график ослабления фильтров разного порядка? Перечислите основные свойства полиномов Чебышева.
10.Какой вид имеют лестничные LCсхемы полиномиальных ФНЧ? Как опре-
делить параметры элементов по заданной передаточной функции?
11.В чем заключается метод частотного преобразования? Как по передаточной
функции ФПНЧ найти передаточную функцию ФВЧ, ППФ и ПЗФ?
12.Как преобразовать схему ФПНЧ в схему ФВЧ, ППФ, ПЗФ? Как преобразовать график ослабления ФПНЧ в графики ослабления перечисленных фильтров?
13.В чем заключаются преимущества и недостатки ARC фильтров в сравнении
с LCфильтрами?
14.Почему ARC фильтры реализуют путем каскадно-развязанного соедине-
ния звеньев низкого порядка (обычно не выше второго)?
15.Как используется метод частотного преобразования при расчете ARC
фильтров? Как рассчитывают параметры элементов ARC звеньев?
16.В чем состоит метод уравнивания коэффицентов?
17.Как найти передаточную функцию ARCзвена, построенного по методу
АВТ?
18.Как реализовать передаточную функцию ARCзвеном, построенным по методу АВТ?
19.Что понимают под чувствительностью характеристик электрических цепей? Как по передаточной функции рассчитать параметрическую чувствительность
АЧХ и ФЧХ цепи?
Приложение 1
Аналитические выражения для параметров
ФПНЧ с характеристиками Баттерворта
1.Режим двусторонней нагрузки:
2. Режим односторонней нагрузки:
Аналитические выражения для параметров
ФПНЧ с характеристиками Чебышева
Режим двусторонней нагрузки
Режим односторонней нагрузки
Приложение 2
Операторная передаточная функция полиномиального ФПНЧ
ОПФ ФПНЧ имеет вид
где
-
полином Гурвица,
-
его корни.
При аппроксимации по Баттерворту
При аппроксимации по Чебышеву
,
Известно, что полином Гурвица может быть представлен в виде произведе- ния линейных и квадратичных сомножителей.
Для четных n -
Для нечетных n-
Для фильтров с характеристикой Баттерворта
Для фильтров с характеристикой Чебышева
Формулы для расчета
и
приведены в Приложении 1.
Приложение 3
Передаточные функции ARC звеньев структуры АВТ
Элементный базис аналоговой вычислительной техники, позволяющий ре-ализовать любую передаточную функцию, включает в себя инвертирующие уси- лители, усилители-сумматоры, интеграторы и интеграторы-сумматоры [1,4]. Основой каждого из перечисленных функциональных узлов АВТ является операционный усилитель (ОУ).
Упрощенные варианты схемного изображения ОУпоказаны на рис.П.3.1.
Рис.П.3.1
В первом приближении ОУ может быть представлен схемой замещения в виде ИНУН (рис.П.3.2).
+ + U1
+ Uвых
U2
Рис.П.3.2
Выходное
напряжение ОУпрямо пропорционально
разности напряжений на неинвертирующем
(+) и инвертирующем (-) входах :Uвых
=
(U2-U1), где
- коэффициент усиленияОУ(коэффициент управленияИНУН).
На практике, в том числе и в ARC звеньях, могут применяться несимме- тричные схемы включенияОУ, приведенные на рис.П.3.3.
+ Uвых + U2 U2 Uвых + + U1 Uвых + + а) б)
в)
Рис.П.3.3
1) Схема с инверсией входного напряжения (рис.П.3.3,а). Положив в схе- ме замещенияОУ(рис.П.3.2)U2 = 0, получимUвых= -U1.
2) Схема без инверсии входного напряжения (рис.П.3.3,б). В этом случаеU1 = 0 иUвых =U2.
3) Схема повторителя напряжения (рис.П.3.3,в). ЗдесьU1 =Uвых=U2.
На рис.П.3.4 показана обобщенная схема, пригодная для реализации любо-го из перечисленных выше элементов АВТ.
Z11 + Z0
U11 U12 U21 U22 Uвых
=
(U4
– U3) Z12 Z22 Z21 4 3 U4 U3 + + + + + +
Рис.П.3.4
Связь между выходным и входными
напряжениями
нетрудно
получить методом узловых напряжений,
составив уравнения для третьего и
четвертого узлов:
Uвых
.
.
Далее, полагая равными нулю те или иные входные напряжения, при опре- деленных значениях операторных сопротивлений можно получить схемы раз- личных устройств АВТ.
Инвертирующий усилитель:U12=U21=U22=0;Z21=Z22=0;Z12;
Z11=R11;
Z0=R0.
При этомUвых
Схема усилителя приведена на
рис.П.3.5.
R0
U11 Uвых + + R11
Рис.П.3.5
Неинвертирующий усилитель: U11=U12=U22=0;Z12;Z22;Z21=0;Z0=R0;Z11=R11.
В этом случае:Uвых
Схема усилителя представлена на
рис.П.3.6.
U21 Uвых + + R0 R11
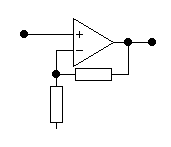
Рис.П.3.6
Взвешенный сумматор с инверсией
входных напряжений:U21=U22=0;Z21=Z22=0;Z11=R11;Z12=R12;Z0=R0.
При этомUвых
Схема сумматора приведена на рис.П.3.7.
+ R11 R0
U11 U12 Uвых + + R12
Рис.П.3.7
Сумматор без инверсии входных напряжений:U11=U12=0;Z12;Z11=R11;Z21=R21;Z22=R22,Z0=R0. При этом
+ R21
Cхема сумматора при-ведена
на рис.П.3.8.
+ U21 Uвых U22 + R22 R11 R0
Рис.П.3.8
Алгебраический сумматор: U12=0;Z12;Z11=R11;Z21=R21;Z22=R22;Z0=R0, тогда
Uвых
Схема сумматора представлена на рис.П.3.9.
R11 R0
U21 U22 + U11 Uвых + + + R22 R21 Рис.П.3.9
Интегратор:U12=U21=U22=0;Z21=Z22=0;Z12;Z11=R11;Z0=1/pC0.
При этомUвых
Схема интегратора приведена на рис.П.3.10.
C0
U11 Uвых + + R11
Рис.П.3.109
C0
Схема интегратора-сумматора представлена
на рис.П.3.11.
Uвых U12 + + + U11 R11 R12
Рис.П.3.11
Следует иметь ввиду, что ARCзвенья могут содержать функциональные блоки, схемы которых отличаются от приведенных на рисунках П.3.5П.3.11. В этом случае связь между входными и выходными напряжениями можно полу-чить либо соответствующим преобразованием обобщенной схемы (рис.П.3.4), либо непосредственно методом узловых напряжений.
В качестве примера найдем выражение передаточной функции ARCзвена, схема которого приведена на рисунке П.3.12.
R8 3
R4 R2 R5 R1 R6 R7 C1 C2 C3 1 2 U1 U2 + + Рис.П.3.12 2 3 4
Представим схему звена (рис.П.3.12) в виде совокупности трех блоков, ис-пользуя следующее правило: каждый блок содержит только один ОУ, выход которого одновременно является выходом блока. Входы блока соединены с вы-ходами других блоков и, возможно, со входом звена.
Блок 1– нестандартный. Для того, чтобы найти связь между его выход-ным напряжениемU2 и входными напряжениямиU1,U3, в схеме (рис.П.3.4) сле-дует положитьU21=U22=0;U11=U3;U12=U1;Z21=Z22=0;Z11=R4;Z12=1/pC1;Z0=1/pC2, тогда
(П.3.1)
Блок 2– алгебраический сумматор (рис.П.3.9), поэтому
(П.3.2)
Блок 3– интегратор-сумматор (рис.П.3.11), следовательно:
(П.3.3)
Подставив (П.3.3) в (П.3.2), а затем (П.3.2) в (П.3.1), получим
.
Домножив
обе части последнего равенства на
,
найдем операторную переда-
точную функцию
Выражения для АЧХ и ФЧХ звена можно
получить, используя связь комп-лексной
и операторной передаточных функций:
Литература
1.Артым А.Д., Белецкий А.Ф. Синтез линейных электрических цепей.
Учебное пособие. –Л: ЛЭИС,1981.- 77с.
2.Собенин Я.А. Расчет полиномиальных фильтров. – М: Связьиздат,1963.
-312с.
3.Матханов П.Н. Основы синтеза линейных электрических цепей. Учебное пособие для радиотехнич. и электротехнич. специальных вузов. М.,Высшая школа, 1976. –208с.
4.Мошиц Г., Хорн П. Проектирование активных фильтров. –М: Мир,1984.
- 320с.
5.Букашкин С.А., Власов В.П., Змий Б.Ф. и др.; Под ред. Ланнэ А.А. Спра-
вочник по расчету и проектированию ARC-схем. – М: Радио и связь, 1984. –308с.
6.Знаменский А.Е., Теплюк И.Н. Активные RC– фильтры. – М: Связь, 1970.
-280с.
4.Галямичев Ю.П., Ланнэ А.А. и др. Синтез активных RC-цепей. – М: Связь,
1975. –296с.